普通城门洞断面正常水深的近似计算式

张宽地，吕宏兴，赵延风

普通城门洞断面正常水深的近似计算式

张宽地1，2，吕宏兴1，赵延风1

（1.西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100；2.中科院水利部水土保持研究所黄土高原土壤侵蚀与旱地农业国家重点实验室，陕西杨凌 712100）

普通城门洞形过水断面是泄洪隧洞较常采用的断面形式之一，其几何图形由槽形与圆弧曲线构成，过水断面水力要素为分段函数，正常水深的计算无论是查图表法还是迭代试算法都比较繁琐，计算误差较大，且依赖图表，不便于应用。为此，通过城门洞形断面均匀流方程的数学变换，并对引入的无量纲参数与相对临界水深的关系进行分析及计算，应用逐步优化拟合原理进行分段拟和，得到了城门洞形断面均匀流水深的直接计算式。实例计算及误差分析表明：在工程实用范围内（正常水深与拱顶半径之比在1.00到1.80之间），该公式最大相对误差仅为0.40%，且该式物理概念清晰明确、公式形式简捷，能为工程设计及水工设计手册的编制提供有益的参考。

水力计算；正常水深；城门洞形断面

1 概 述

普通城门洞形过水断面是泄洪隧洞和灌溉引水隧洞较常采用的断面形式之一，水力计算中的正常水深的计算是工程设计中的关键水力要素，应用十分频繁且有较高的精度要求。对于普通城门洞形断面临界水深的计算目前已经有较好的计算方法，如张生贤（1992年）提出的明渠临界流β代换简捷计算法，采用数表法求不同断面的临界水深；马吉明等（2000年）提出了查图法；王正中等（2004年）提出了一种近似计算公式；赵延风等（2008年）提出了新的近似计算公式［1－6］。但普通城门洞断面正常水深的计算为分段函数，且为超越函数，故其计算方法较少。现行的有关普通城门洞形断面明渠正常水深计算方法有《水工设计手册》的图解法、试算法；梁勋、文辉等分别在2005年、2007年提出了不同的近似计算公式［7，8］。但图解法、试算法依赖于图表，计算误差大，不易推广，而直接计算法在追求精度的同时却忽视了公式的简捷性，使公式形式非常复杂，不便于工程界采用。因此，本文在总结原有成果的基础上，通过数学推导及逐步优化拟合，提出了普通城门洞形断面正常水深计算的新近似公式，该公式不仅具有精度高，适用范围广等特点，且物理概念清晰明确，公式形式非常简捷、直观，便于工程界采用。

2 明渠均匀流水深的基本方程

城门洞形过水断面无压流顺坡渠段可按恒定均匀流计算，采用明渠均匀流计算公式计算其正常水深，以曼宁公式表示的明渠均匀流方程为［4］

式中：Q为流量（m3／s）；i为底坡；n为糙率；A0为过水断面面积（m2）；χ为湿周（m）。

2.1 城门洞形断面水力要素

城门洞形断面的形式见图1，对于水深小于H0的情况属于矩形断面正常水深的求解问题，这里不再罗列。当均匀流水深h0大于边墙高度H0时，属于本文研究的内容，其水力要素为

图1 城门洞形隧洞断面Fig.1 Arched water transfer cross section

当城门洞形隧洞侧墙高度H0等于顶拱半径r，θ＝π／2时，此断面称为普通城门洞断面，将其代入公式（2）得

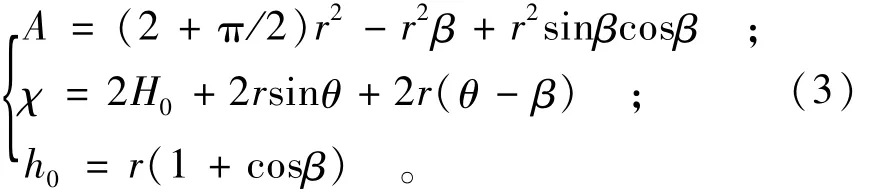
2.2 普通城门洞形断面均匀流方程

将上式（3）对应的水力要素代人公式（1），并整理便得求解城门洞形断面正常水深的非线性方程

由此可知，普通城门洞断面正常水深的计算就是非线性方程（4）的求根问题，现行有关普通城门洞形断面明渠正常水深计算方法主要是《水工设计手册》的图解法、试算法［1，2］；但上述方法依赖于图表，计算误差大，不易推广。因此，寻求一种形式简捷、计算误差小的近似公式来逼近普通城门洞形断面均匀流方程组不妨为一种较好的求解思路。梁勋、文辉［7，8］等提出的近似计算公式就是很好的探索，但两公式在追求精度的同时都忽视了公式形式的简捷性，提出的计算公式形式非常复杂，不便于工程界应用。

3 普通城门洞形断面正常水深的直接计算式

将上式（4）均匀流方程组进行恒等变形，可得正常水深精确计算公式

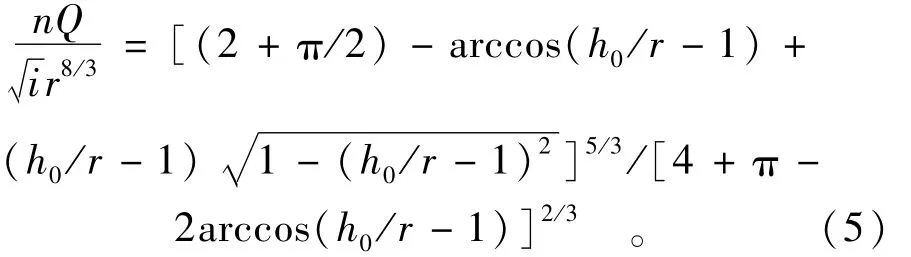
上式（5）为超越函数且未知数包含在三角函数中，无法直接求解，为得到近似计算公式，不妨引入无量纲参数

理论上的取值范围为 x＝［0，2］，为避免波状水面有可能接触洞顶引起水流封顶现象或明满流交替现象［4］，对自由水面以上的净空面积要求不小于全断面面积的15%，净空高度不小于0.4 m［1］，可得相对无量纲水深x的最大值一般不超过1.80，相应地可得无量纲参数k值的上限为2.38。根据正常水深连续性可知，x的最小值为1.0，相应无量纲参数k的取值范围k＝［1.26，2.38］，在 x的取值范围内以一定步长给定一组数值代入均匀流方程（5）可得相应无量纲参数k的取值，本文作者对该范围内k与x的1 000多组数据采用Matlab7.1软件进行逐步优化拟合，得出以下直接计算公式：

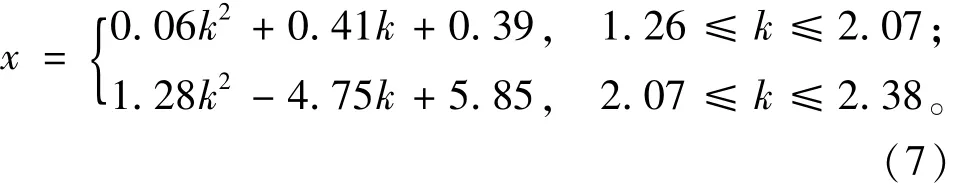
4 精度评价

为验证本文计算公式的正确性及误差全程分布情况，通过给定不同的x值，由水力要素函数求得相应x的不同过流流量Q，再由均匀流方程求得相应无量纲参数k值，最后将k值代入直接计算公式（7）求得相应无量纲水深x的计算值。设精确解为x*，则相对误差 Δ＝（x－x*）／x*×100%。为简明起见，图2绘制出了本文公式（7）在相对正常水深x取值范围的误差全程分布情况。由图2可知，本文公式精度完全满足工程的需求，在工程实用范围内（正常水深与拱顶半径之比在1.00到1.80之间）最大误差绝对值为0.40%。

图2 公式（7）相对误差全程分布图Fig.2 The distribution of relative error by using formula（7）

有关计算城门洞断面正常水深的直接计算方法主要有梁勋公式和文辉公式。但因梁勋公式与本文研究的断面形式略有差异，故不再列出，表1仅列出文辉公式和本文计算公式，进行比较。

从公式的形式来看，文辉公式中第一项系数接近于零，但指数又非常大，导致计算结果稳定性较差；而本文公式形式为分段二次多项式，相对简捷。从公式的适用范围来看，本文公式与文辉公式适用范围一致。从适用范围内最大相对误差来看，文辉公式最大相对误差最小，本文公式次之，但在实际工程设计与渠道原型观测中，误差小到一定程度是没有意义的，且本文公式中最大相对误差的绝对值为0.40%，远满足工程实际需要。因此，从公式的简捷性、公式适用范围及适用范围内最大相对误差三方面综合考虑，本文公式（7）是目前计算该断面正常水深的较好公式。

表1 不同计算方法的比较Table 1 Comparison of results obtained by different methods

5 应用举例

某水库输水隧洞，设计引水流量28 m3／s，拟用普通城门洞形断面，初设半径为2.5 m，底坡i＝1／2 500，n＝0.014。试计算洞内的均匀流水深，计算步骤如下。

步骤1：计算无量纲参数k，

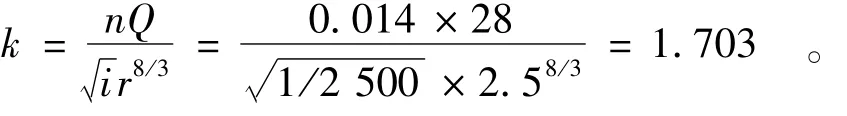
步骤2：将无量纲参数代入公式（7），计算无量纲水深 x，因1.26≤k≤2.07，代入如下公式计算相对正常水深，

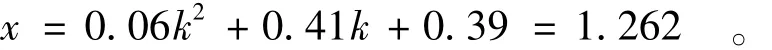
步骤3：将无量纲水深代入公式（6）计算正常水深h0，

精确解为3.156 m，相对误差为－0.032%。

6 结 论

针对现有普通城门洞断面正常水深求解公式存在公式复杂的缺陷，本文应用逐步逼近原理，在分析均匀流方程数学特性的基础上，提出了普通城门洞形断面正常水深的直接计算公式，该算法与目前文献研究的成果相比具有表达式简捷、准确、适用范围广等特点，克服了查图、查表法的繁琐、误差大等缺点，是目前计算普通城门洞断面正常水深的较好计算公式，能为水工设计人员及水工计算手册的编制提供有益的参考。

［1］ 清华大学.水力学（修订本）（上册）［M］.北京：高等教育出版社，1980.（Tsinghua University.Hydraulics［M］.Beijing：Higher Education Press，1980.（in Chinese））

［2］ 吴持恭.水力学［M］.北京：高等教育出版社，1979.（WU Chi-gong.Hydraulics［M］.Beijing：Higher Education Press，1979.（in Chinese））

［3］ 张生贤，张步南.明渠均匀流临界流β代换简捷计算法［C］∥中国科学技术协会首届青年学术年会论文集.北京：中国科学技术出版社，1992.（ZHANG Sheng-xian，ZHANG Bu-nan.The simpleβdisplacement computation method of open channels uniform flow and critical flow［C］／／The First Youth Learning Annual Corpus of China Association for Science and Technology.Beijing：China Science Technology Press，1992.（in Chinese））

［4］ 马吉明，梁海波，梁元博，等.城门洞形及马蹄形过水隧洞的临界水流［J］.清华大学学报，1999，39（11）：32－34.（MA Ji-ming，LIANGHai-bo，LIANGYuan-bo，et al.Critical flow in city－gate and horseshoe conduit［J］.Tsinghua Univ：Sci and Tech，1999，39（11）：32－34.（in Chinese））

［5］ 王正中，陈 涛，张新民，等.城门洞形断面隧洞临界水深的近似算法［J］.清华大学学报（自然科学版），2004，44（6）：814－816.（WANG Zheng-zhong，CHEN Tao，ZHANG Xin-min，et al.Approximate solution for the critical depth of a arched tunnel［J］.J Tsinghua Univ：Sci and Tech，2004，44（6）：814－816.（in Chinese））

［6］ 赵延风，宋松柏，孟秦倩.普通城门洞形断面临界水深的近似计算方法［J］.长江科学院院报，2008，25（4）：14－15.（ZHAOYan-feng，SONGSong-bai，MENG Qin-qian.Approximate method calculating critical water depth in common city-opening shaped cross-section［J］.Journal of Yangtze River Scientific Research Institute，2008，25（4）：14－15.（in Chinese））

［7］ 梁 勋，冯玉莲.标准门洞型过水断面水力计算方法的简化［J］.黑龙江水专学报，2005，32（2）：18－20.（LIANG Xun，FENG Yu-lian.Simplification of hydraulic calculation method of the cross section for standard door type tunnel［J］.Journal of Heilongjiang Hydraulic Engineering College，2005，32（2）：18－20.（in Chinese））

［8］ 文 辉，李风玲，欧军利，等.城门洞形断面隧洞正常水深的近似算法［J］.给水排水，2007，33（7）：25－28.（WEN Hui，LI Feng-ling，OU Jun-li，et al.Approximate solution of the normal depth inside tunnel with arch cross-section［J］.Water and Wastewater Engineering，2007，33（7）：19－21.（in Chinese） ）

Approximate Method Calculating Normal Depth of Arched-gate Section Tunnel

ZHANG Kuan-di1，2，LV Hong-xing1，ZHAO Yan-feng1
（1.College of Water Resources and Architectural Engineering，Northwest A＆F University，Yangling 712100，China；2.Institute of Soil and Water Conservation，CAS.，Yangling 712100，China）

It is difficult to calculate normal water depth of a arched section tunnel for its complex geometrical shape.From using the mathematics transformation method and the theory of optimization and regression to deal with the basis equation of the normal depth in arched section tunnel，a new direct formula is derived in this paper，which overcomes the shortage of other methods，such as chart looking up method，trial and error method and iterative trial method.This method is simpler and more accurate than other approximate methods with a maximum error of less than 0.40%in the utility range（ratio of critical depth to arch radius of 1.0－1.80）.So，it will be useful in engineering practice and in course of compiling handbook of hydraulic structure design.

hydraulic calculation；normal depth；arched section tunnel

TV131

A

1001－5485（2010）02－0034－03

2009-01-06；

2009-03-19

国家973计划课题（2007CB407201）；国家自然科学基金重点项目（40335050）

张宽地（1978-），男，宁夏隆德人，讲师，博士研究生，主要从事水工水力学及坡面水流的研究，（电话）13519149639（电子信箱）zhangkuandi428＠126.com。

（编辑：曾小汉）