地震作用下渡槽槽架结构位移控制的可靠度研究

安旭文，张明强，朱 暾

地震作用下渡槽槽架结构位移控制的可靠度研究

安旭文1，张明强2，朱 暾1

（1.武汉大学土木建筑工程学院，武汉 430072；2.长江勘测规划设计研究院交通工程设计咨询公司，武汉 430010）

以渡槽槽架结构的层间位移和顶点位移作为控制标准，提出了渡槽槽架结构在小震作用下位移控制的可靠度分析模型；基于现行相关规范，提出了渡槽槽架结构的层间位移和顶点位移控制限值；根据各随机变量的统计特征，采用Monte-Carlo模拟与有限元相结合的方法对渡槽槽架结构体系位移控制的可靠度进行了研究，为渡槽结构在地震作用下的可靠度分析和设计提供了一种新方法。

小震；渡槽结构；弹性侧移；Monte-Carlo模拟；有限元；体系可靠度

唐山大地震后，我国地震工程界明确提出了土木工程三水准的抗震设防目标，在设计中采用二阶段的设计方法实现。第一阶段设计是取小震作用下的地震动参数计算结构的弹性地震作用标准值和相应的地震作用效应，对结构构件的承载力和弹性变形进行验算，实现第一、二水准的设防要求；第二阶段是对有特殊要求的结构以及地震时易倒塌的结构，按照大震下的地震动参数，对结构的弹塑性层间变形进行验算，实现第三水准的设防要求。目前，国内外对于渡槽结构抗震计算理论的研究还比较少［1］，对于渡槽结构在地震作用下可靠度问题的研究则更少，因此，对渡槽结构在多遇地震下位移控制的可靠度进行研究是非常必要的。

地震作用的统计规律不仅与地面运动的参数有关，而且是与时间有关的随机过程。严格来说，结构在地震作用下的可靠度分析应将地震作用看作随机过程，采用动力可靠度理论进行分析。但考虑到动力可靠度的计算难度较大，为简化计算，我国规范GB 50011－2001《建筑抗震设计规范》［2］将这种随机过程转化为设计基准期内的最大值，这个最大值是与时间无关的随机变量。然后按“拟静力法”确定结构在地震作用下的效应值，并以此作为结构抗震设计的依据。借鉴这一方法，本文亦将渡槽结构在地震作用下的可靠度分析问题转化为静力可靠度进行分析。同时，以渡槽槽架结构的侧向位移作为控制指标，建立槽架结构在正常使用极限状态下的抗震可靠度分析模型和计算方法，对其在小震作用下位移控制的可靠度进行分析。

1 位移控制可靠度的计算模型及计算方法

在水平地震作用下，渡槽槽架结构的层间或顶层最大位移与槽架梁、柱等构件的截面尺寸、材料弹性模量，以及作用在结构上的荷载之间存在一定的关系，但其关系式不能明确地表达，其功能函数一般可表述为

式中：［u］为小震作用下结构层间位移限值或顶点位移限值，计算中按常量处理；umax（·）为在地震作用下结构分析计算得到的最大层间位移或顶点位移；lbi，bbi，hbi分别为第 i根梁的计算跨度、截面宽度和截面高度；lcj，bcj，hcj分别为第 j根柱的计算高度、截面宽度和截面高度；n，m分别为梁和柱的总数；Ec为梁、柱混凝土的弹性模量；P是作用在结构上的地震作用和其它荷载。

在上述位移功能函数的可靠度分析中，结构层间或顶点最大位移umax是各梁、柱的几何尺寸和材料弹性模量的高阶非线性隐式函数，无法用显式表达。对于这一类功能函数不能明确表达的结构可靠度计算问题，本文采用Monte-Carlo模拟与有限元相结合的方法计算其可靠度。

2 槽架结构的位移控制取值及位移计算方法

2.1 位移控制值的确定

在渡槽结构的抗震设计中，必须对其侧向位移加以限制，这个限制实际上是对构件侧向刚度的一个相对控制指标。为判断建筑结构的侧向刚度，目前国内外都是采用一个简单且又能准确反映建筑结构整体侧向刚度的参数——水平位移指标，定义该指标为结构顶点最大水平位移Δmax与结构总高度H的比值，即Δmax／H，用于控制建筑物的整体变形；层间最大水平位移umax与该层高度lc的比值（即umax／lc），用于控制建筑物的局部变形。

结构的水平位移一般是根据建筑结构的材料、结构型式并结合实际工程经验和大量的试验资料经统计分析确定的。渡槽槽架结构属于典型的剪切型结构，采用层间位移与层高度的比值umax／lc作为控制指标能够较好地反映槽架结构的实际变形性能。根据JGJ 3－2002［3］对框架结构层间位移的取值规定以及原规范JGJ 3－91《钢筋混凝土高层建筑结构设计与施工规程》［4］对框架结构顶点位移指标限值和层间位移指标限值的规定，本文在可靠度计算中，将结构层间最大水平位移umax与该层高度lc的比值umax／lc、顶点最大位移 Δmax与总高度 H的比值Δmax／H的控制值分别取为 1／450，1／500和1／550。

2.2 位移计算方法

由于渡槽槽架结构承受的荷载主要集中在槽架顶部，因此，可将槽架结构视为单自由度体系，根据达朗贝尔原理，地震作用下其线弹性振动方程为

式中：［M］为结构节点质量矩阵；［C］为阻尼矩阵；［K］为结构的刚度矩阵；｛x｝，｛｝，｛｝分别为质点的相对位移、相对速度、相对加速度列向量；｛｝为地震地面运动的加速度。

根据结构的运动方程，首先按照振型分解反应谱法，根据抗震设防烈度、场地类别和设计地震分组以及结构自振周期确定结构上的地震作用，然后按拟静力法计算结构各节点的位移。

3 基本变量的统计特征

3.1 地震作用的概率模型与统计参数

根据我国华北、西北和西南地区的地震危险性分析结果，文献［5，6］对我国地震烈度和地震作用的概率分布进行了统计分析，运用概率的方法对地震作用的概率意义和取值进行了分析计算。从地震烈度的重现期来看，GB 50011－2001规定，在设计基准期50年内，超越概率为63.2%的地震为多遇地震；超越概率为10%的地震为基本设防烈度的地震；超越概率为2%～3%的地震为罕遇地震。对于某一给定强度的地震作用Ei下，地震作用的变异性主要由动力系数的变异性决定，考虑动力系数的离散性，通过对国内外的强震记录反应谱进行统计分析，可认为等效地震作用效应VE的条件概率分布是符合极值Ⅰ型分布的，其数学表达式为

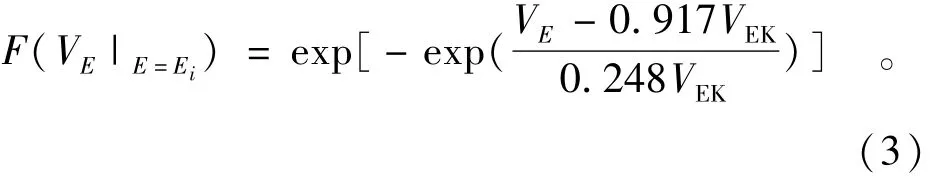
式中，VEK为结构等效地震作用标准值。

设计基准期T内发生某强度地震的条件下，地震作用的平均值 μET＝1.06VEK，变异系数为 δET＝0.30。

3.2 其他变量的统计特征

由功能函数（1）可以看出，影响渡槽槽架结构顶点位移或层间位移的基本变量主要有槽架梁、柱的截面尺寸，结构组成材料的弹性模量Ec以及作用在槽架结构上的各种荷载。在位移计算中不考虑梁、柱配筋对构件截面刚度的影响。

根据文献［7］的统计分析，认为梁（柱）截面宽度和高度均服从正态分布，其中截面宽度bb（bc）的均值系数和变异系数分别为1.0和0.01；截面高度hb（hc）的均值系数和变异系数分别为1.0和0.02。

作用在渡槽结构上的荷载（或作用）主要考虑结构自重、槽内水重和地震作用。结构自重的均值系数为1.05，变异系数为0.06，概率分布类型按正态分布考虑；槽内水重的均值系数为1.00，变异系数为0.05，其概率分布类型服从对数正态分布［7］。对于混凝土的弹性模量Ec，在可靠度计算中，一般按定值处理［8］。各随机变量的统计特征列于表1。

表1 随机变量的统计特征Table 1 Statistical character of stochastic variables

4 可靠度计算步骤及计算实例

4.1 可靠度计算步骤

根据渡槽结构在小震作用下位移可靠度的分析模型，采用按Monte-Carlo模拟法与有限单元法相结合的方法，对渡槽结构的位移可靠度进行计算分析。具体计算步骤如下：

（1）根据渡槽结构上作用的荷载和构件截面尺寸等随机变量的标准值乘以各自的均值系数，求得各随机变量的均值 μxi（i＝1，2，…，n）和均方差 σxi；

（2）根据各基本变量的统计参数μxi，σxi及其概率分布类型，采用Monte-Carlo模拟法抽样产生一系列符合各自概率分布类型的随机数列，且假定各随机变量之间相互独立；

（3）将构件截面尺寸的随机数列作为结构构件的实际截面尺寸，作用荷载的随机数列作为结构上作用的实际荷载，按有限单元法求解结构的顶点位移和层间位移；

（4）判断水平位移限值与位移计算值的相对大小，若计算值大于限值，则结构失效一次，若计算值小于限值，则结构可靠；

重复第（2）至（4）步N次，每一次模拟，都经过一次判断，如果位移计算值大于限值，则结构失效次数nf增加一次，当N次模拟结束后，利用公式Pf＝nf／N可求得结构的失效概率。

4.2 计算实例及结果分析

某钢筋混凝土简支梁式渡槽［9］，槽架肢柱截面尺寸为300 mm×400 mm，槽架梁截面尺寸为250 mm×400 mm，槽架柱中心距为3.16 m。渡槽槽架梁、柱混凝土强度等级均为C20，其弹性模量为Ec＝2.55×104N／mm2。各层结点上作用的荷载如图1所示。图中，Gk为渡槽传来的自重标准值；Qk为渡槽传来的水重标准值；PEk为作用在槽架顶部的地震作用标准值。

图1 渡槽槽架结构分析模型Fig.1 The analytical model of an aqueduct frame structure

根据渡槽结构体系在小震作用下位移可靠度的计算方法和计算步骤，分别按抗震设防烈度7度和8度对上述槽架结构的可靠度进行了计算，求得槽架结构在槽内无水和槽内有水时，不同位移控制指标下的失效概率Pf，这里以20万次模拟结果作为渡槽结构位移失效概率的最终估算值，计算结果如表2所示。

表2 槽架结构在小震作用下位移控制的失效概率P fTable 2 Failure probability controlled by displacement of an aqueduct structure in small earthquake P f

由表2的计算结果可以看出：

（1）对于同一位移限值，不论是槽内满水还是槽内无水，层间位移的失效概率明显高于结构顶点位移的失效概率。设计中应注意加强槽架结构层间的抗剪切刚度。

（2）在地震作用下，槽内满水时渡槽结构层间位移和顶点位移的失效概率大于槽内无水时的失效概率。设计中应主要以槽内满水防震为依据。

（3）随着位移控制指标的减小，槽架结构的抗侧移失效概率逐渐增大。设计中应慎重确定位移控制指标。

（4）抗震设防烈度为8度时，槽架结构位移控制的失效概率远高于7度设防时的失效概率。因此，渡槽设计中首先根据设防烈度和位移控制标准用本文方法确定构件截面尺寸，充分满足侧向刚度的要求，然后再按承载力要求进行截面配筋计算。这样不仅可以充分发挥材料的强度，同时结构的侧移刚度也满足要求，使设计的渡槽结构的不同控制指标具有较佳的可靠度一致性，达到既节约材料又安全可靠的目的，可供工程设计参考。

5 结 语

本文以渡槽槽架结构的顶点位移和层间位移作为控制标准，提出了渡槽槽架结构在小震作用下位移控制的可靠度分析模型，给出了相应的计算方法和计算步骤。基于现行规范的有关规定，根据地震作用的统计特征，以设计参数作为基本变量，对不同烈度下渡槽槽架结构以位移控制的可靠度进行计算。计算结果符合一般规律，可供类似渡槽工程设计参考。

［1］ 李正农，袁文阳，秦明海.渡槽抗风抗震计算与分析［M］.武汉：湖北科学技术出版社，2001.（LI Zhengnong，YUANGWen-yang，QIN Ming-hai.Aqueduct Calculation and Analysis in Wind and Seismic［M］.Wuhan：Hubei Province Press of science and technology，2001.（in Chinese））

［2］ GB 50011－2001.建筑抗震设计规范［S］.北京：建筑工业出版社，2001（GB 50011－2001.Code for Seismic Design of Buildings［S］.Beijing：China Architecture＆Building Press，2001.（in Chinese））

［3］ JGJ 3－2002.高层建筑混凝土结构技术规程［S］.北京：中国建筑工业出版社，2003.（JGJ 3－2002.Technical Specification for Concrete Structures of Tall Building［S］.Beijing：China Architecture＆Building Press，2003.（in Chinese））

［4］ JGJ 3－91.钢筋混凝土高层建筑结构设计与施工规程［S］.北京：中国建筑工业出版社，1991.（JGJ 3－91.Design and Construction Specification for Reinforced Concrete Structures of Tall Building［S］.Beijing：China Architecture＆Building Press，1991.（in Chinese））

［5］ 高小旺，鲍霭斌.地震作用的概率模型及其统计参数［J］.地震工程与工程振动，1985，（1）：13－22.（GAO Xiao-wang，Bao Ai-bin.Probabilistic model and its statistical parameters for seismic load［J］.Earthquake Engineering and Engineering Vibration，1985，（1）：13－22.（in Chinese））

［6］ 高小旺，鲍霭斌.用概率方法确定抗震设防标准［J］.建筑结构学报，1986，（2）：55－63.（GAO Xiao-wang，BAO Ai-bin.Determination of anti-seismic level by probabilistic method［J］.Journal of Building Structures，1986，（2）：55－63.（in Chinese））

［7］ 黄振兴，程学文，侯建国.水工钢筋混凝土结构可靠度分析和分项系数确定［C］∥水利水电工程结构可靠度设计统一标准专题文集.成都：四川科学技术出版社，1994：34－62.（HUANG Zhen-xin，CHENG Xue-wen，HOU Jian-guo.Reliability analysis and the determination of partial factors for hydraulic reinforced concrete structures［C］∥Special Thesis of Unified Design Standard for Reliability of Hydraulic Engineering Structures.Chengdu：Sichuan Province Press of science and technology，1994：34－62.（in Chinese））

［8］ 张学易.水工混凝土的强度特性 ［C］∥水利水电工程结构可靠度设计统一标准专题文集.成都 ：四川科学技术出版社，1994：63－67.（ZHANG Xue-yi.Strength characteristic of hydraulic concrete［C］∥Special Thesis of Unified Design Standard for Reliability of Hydraulic Engineering Structures.Chengdu：Sichuan Province Press of science and technology.1994：63－67.（in Chinese））

［9］ 赵文华，陈德亮，颜其照，等.渡槽（第二版）［M］.北京：水利电力出版社，1989.（ZHAO Wen-hua，CHEN De-liang，YAN Qi-zhao，et al.Aqueduct（Edition 2）［M］.Beijing：Water and Power Press，1989.（in Chinese） ）

Reliability Controlled by Displacement of Aqueduct Frame Structure System Subjected to Earthquake

AN Xu-wen1，ZHANG Ming-qiang2，ZHU Tun1
（1.School of Civil Engineering，Wuhan University，Wuhan 430072，China；2.Changjiang Institute of Survey，Planning，Design and Research，Wuhan 430010，China）

Taking inter-storey and peak displacements of an aqueduct frame structure as a control index，the reliability model of the aqueduct structure controlled by horizontal displacement subjected to a small earthquake was built.On the basis of the relative specifications，the limit values of inter-storey and peak displacements were put forward.According to the statistical characteristics of design parameters，the reliability controlled by displacement of the aqueduct structure system under a small earthquake has been studied using the method combining Monte-Carlo simulation with finite element.A new reliability analysis and design method of aqueduct structure under earthquake action was put forward.

small earthquake；aqueduct frame structure；elastic displacement；monte-carlo simulation；finite element；system reliability

TV31

A

1001－5485（2010）02－0075－04

2009-04-01

安旭文（1970-），男，甘肃民乐人，副教授，博士，从事结构可靠度理论与应用研究，（电话）027-68772388（电子信箱）axw002＠163.com。

（编辑：刘运飞）