基于敏感度和发生概率联合熵的投资项目风险决策

王 华， 李 勇， 金 磊

(沈阳工业大学 a. 工程项目评价与管理研究所， b. 建筑工程学院， 沈阳 110870)

投资项目决策问题是一个在多因素、非线性随机环境下进行风险决策的问题。由于在投资项目风险评价中风险因素的发生是随机的，各风险因素的发生是非线性和非独立的，所以传统的多因素敏感性分析方法存在着缺陷。首先，传统的敏感性分析方法没有考虑到各种不确定性因素发生时的非线性特点，多采用线性分析方法；其次，传统的敏感性分析方法没有考虑到风险因素发生的非独立性，在实际经济分析中，这些因素往往同时发生变化或相互依赖地变动，从而导致对指标的影响十分复杂；最后，传统多因素敏感性分析很难同时进行风险因素变化的概率分析，因此在投资风险整体分析和建模方面的研究还很局限，对于投资项目整体的风险评价和决策在方法上是不完善的。为了弥补多因素敏感性分析的不足，本文综合分析投资项目风险因素敏感熵和风险因素发生概率熵，确定投资项目各评价指标的联合熵权，并在此基础上对多个项目进行比较，从而确定最优投资方案。

一、风险因素敏感度的熵评价

1. 基于微分法的敏感度分析

敏感性分析是指从众多不确定性因素中找出对投资项目经济效益指标有重要影响的敏感性因素，并分析、测算其对项目经济效益指标的影响程度和敏感性程度[1]21。国内通常的做法是假定影响项目经济效益的因素中，诸如项目生产能力利用率、销售收入(或产品售价)、变动成本(或原材料和燃料价格)、总投资、固定成本费用等为敏感性因素，在其他敏感性因素不发生变化的情况下，分析某单因素或某双因素发生变化的幅度，从而确定项目经济效益对哪些因素的变化最敏感。从近年来国内投资项目风险分析的方法来看，大多采用线性分析方法来评价项目投资效率[2]，因其没有考虑到各种不确定性因素发生时的非线性特征，导致分析结果缺乏严密性。本文根据不确定性风险因素发生时的非线性特征，采用微分法分析投资项目敏感性因素的敏感程度。

设Y为敏感性分析对象的经济评价指标，可以代表工程项目的净现值、内部收益率、贷款偿还期等经济评价指标；设X1，X2，…，Xm代表资源成本、销售价格、工期、汇率、产量、项目寿命期等影响评价指标的不确定因素[3]；设有通用解析表达式Y=F(X1，X2，X3，…，Xm)，根据对变量微分原理[4-5]

(1)

在实际分析和计算中用偏差近似代替微分

(2)

(3)

本文定义敏感度为

(4)

2. 风险因素敏感度的熵评价

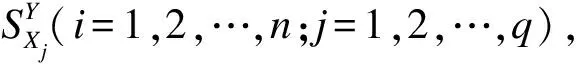
(5)

计算第i项指标的敏感熵

(6)

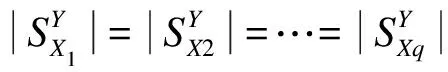
敏感熵ei1从0到1的闭区间取值，反映评价指标对风险变量集不同集值的敏感度。如果用敏感熵来评价一组风险变量在不同集值下的敏感性程度，则熵值越大越敏感，风险性越大。ei1为0时敏感熵最低，这时随机风险变量不产生敏感熵，只有单变量产生敏感度。

二、风险因素的联合熵评价

在投资项目不确定性风险决策中，只考虑敏感性因素的变化幅度或敏感性因素的变化概率都是片面的，因此本文采用联合熵分析方法，从风险敏感度和风险发生概率两个方面对系统的风险性进行综合评价。

设用q个风险因素所构成的风险体系来评价n个待评指标，第i个评价指标的第j个风险因素的风险发生概率为pij(i=1，2，…，n；j=1，2，…，q)，计算第i项指标的发生概率熵

(7)

1. 各评价指标联合熵的确定

在热力学中，用热熵来说明运动过程的不可逆性；在信息学中，用信息熵来度量信息的不确定性。熵具有如下特性：① 可加性。由于熵具有概率性质，所以系统的熵等于其各个状态的熵之和。② 加法性。系统A、B相互独立，系统A的熵为E(A)，系统B的熵为E(B)，则复合系统AB的联合熵E(AB)=E(A)+E(B)，即由相互独立的系统构成的复合系统的熵(联合熵)等于各单独系统熵(边际熵)之和[6]。

根据熵的上述特性，设X和Y为两个分别对应不同后果状态的风险行为，其确定性小于等于二者单独的不确定性之和，即H(X，Y)≤H(X)+H(Y)，当且仅当风险行为X和Y相互独立时，等号成立。如果假设中的风险敏感度和风险发生概率是完全独立的两个风险行为，则两个独立风险的联合熵ei值应为

ei=ei1+ei2(i=1，2，…，n)

(8)

2. 基于联合熵的多方案决策模型

对于投资项目风险决策问题，决策者不但希望收益最大，而且也希望风险最小，即投资收益的标准离差最小，因此投资项目风险决策可转化为多目标决策问题[7]。假设目前共有可投资项目m个，并有评价指标n个构成的评价指标体系，其元素rij为第i方案第j指标的水平。根据专家评价法可以得到这些指标的主观权重为ωj。根据前面已经求得的第j个指标的熵，可以确定各评价指标的熵权

(9)

根据指标的熵权，结合采用专家评价法得到的这些指标的权重ωj，计算指标的综合权

(10)

将可行性方案集映射到“距离”L空间，求出偏差的综合

(11)

在进行优序评价时，若只重视偏差的总和，可取p=1，得

(12)

显然，“距离”小者更接近理想方案，即按照L由小到大进行排序，供决策者参考[8-9]。

通常，在理想方案排序后，有时还不能确定有几个项目可以投资，为此可以建立0-1规划模型[10]。设变量xi=0或1，当xi=0时，表示第i个项目不投资；当xi=1时，表示第i个项目投资。目标函数为

(13)

式中：L(i)——第i个方案的“距离”；

Sij——第i个投资项目对第j种资源的需求；

Sj——第j种资源的总供给，共有k种资源；

Tij——第i个投资项目的第j种期望收益；

Tj——第j种收益最低限，共有l种收益。

在实际应用中，把资源和期望利润代入上面的约束条件中，求解此0-1规划。当xi=1时，则第i个项目可以投资；当xi=0时，则第i个项目不宜投资。

三、案例分析

某企业在投资前进行风险分析，得到评价指标各风险因素仿真敏感度系数(见表1)和对应风险因素的发生概率(见表2)。该企业的投资项目共有4个投资方案，各方案的评价指标值在表3中已经给定。下面根据以上理论对各个方案进行评价。

根据式(5)对各评价指标的敏感度系数进行归一化处理，得到表4。根据式(6)计算各评价指标的敏感熵：e11=0.763 7，e21=0.858 8，e31=0.855 2，e41=0.972 8。

表1 评价指标各风险因素仿真敏感度系数

表2 各评价指标对应风险因素的发生概率

表3 投资项目各方案评价指标值

表4 归一化处理后的敏感度系数

根据式(7)计算各评价指标的发生概率熵：e12=0.457 5，e22=0.486 5，e32=0.471 8，e42=0.343 1。

根据式(8)求得各评价指标的联合熵：e1=1.221 2，e2=1.345 3，e3=1.327 0，e4=1.315 9。

根据式(9)计算各评价指标的联合熵权：d1=0.182 9，d2=0.285 5，d3=0.270 4，d4=0.261 2。

通过专家评价法得到各评价指标的主观权重ωj分别为0.6，0.8，0.5，0.6。

根据指标的联合熵权，结合各评价指标的主观权重ωj，按照式(10)计算指标的综合权

同样可计算出：λ2=0.362 5，λ3=0.214 6，λ4=0.248 8。

将可行性方案集映射到“距离”L空间，根据式(12)求出各项目偏差的综合：

L1=1-(0.7×0.290 3+0.6×0.362 5+

0.6×0.214 6+0.4×0.248 8)=0.648 6

同样可计算出：L2=0.512 5，L3=0.710 9。

显然，“距离”小者L2更接近理想方案，可按照“距离”由小到大进行排序，供决策者参考。排序后，有时还不能确定有几个项目可以投资，为此可以建立0-1规划模型，确定方案是否可行，本文该过程省略。

四、结 论

投资项目的风险决策包括确定性风险决策和不确定性风险决策。不确定性风险决策中的多因素非线性与非独立风险决策是投资项目风险决策与评价的一项重要命题。多数投资项目风险评价中风险因素的发生是随机的，各风险因素的发生是非线性和非独立的，需要在传统多因素敏感性分析研究方法的基础上进行补充和深入研究。本文综合分析投资项目风险因素敏感熵和风险因素发生概率熵，据此确定投资项目各评价指标的联合熵权，是投资项目风险评价的新方法。在相关方面开展后续研究，对于投资项目风险决策的理论与方法体系具有重要的补充意义。

参考文献：

[1]邱菀华.管理决策与应用熵学 [M].北京：机械工业出版社，2002.

[2]杨玉春，孙莉，刘萍，等.创新型企业评价研究 [J].沈阳工业大学学报:社会科学版,2009(3)：234-238.

[3]朱选民.建设项目敏感性分析的临界值法及多因素敏感性分析 [J].数量经济技术经济研究,1994(3)：35-40.

[4]陈仪坤.用微分法进行多因素的敏感性分析 [J].数量经济技术经济研究,1988(9)：19-21.

[5]王旭，曹达强.基于信息熵的工程建设项目风险控制研究 [J].价值工程,2008(6)：31-35.

[6]Alison M，David P.Risk evaluation and its importance to project implementation [J].Work Study，2002，51(4)：202-206.

[7]Jaynes E T.On the rationale of maximum entropy methods [J].IERR，1982，70(9)：539-562.

[8]束金龙.线性规划理论与模型应用 [M].北京：科学出版社,2008.

[9]张国权，李文立，王明征.基于离差函数和联合熵的组合赋权方法 [J].管理学报,2008(3)：32-35.

[10]吴振强，马建峰.基于联合熵的多属性匿名度量模型 [J].计算机研究与发展,2006(7)：23-26.