小波奇异性在钢结构损伤检测中的应用

张 悦,杜守军,张丽梅

(河北科技大学建筑工程学院,河北石家庄 050018)

小波奇异性在钢结构损伤检测中的应用

张 悦,杜守军,张丽梅

(河北科技大学建筑工程学院,河北石家庄 050018)

根据小波奇异性检测理论,以应变能的损伤信号为结构损伤指标,分别以悬臂梁结构、平面桁架结构和空间网架结构为例进行数值模拟,将原始损伤信号和经过小波变换后的损伤信号进行对比,结果证明采用该方法不但对单一损伤而且对多损伤均能有效地识别出结构的损伤位置,表明了该方法的可靠性和实用性。

损伤检测;损伤定位;小波奇异性;应变能;小波变换

随着经济发展和社会进步,人们对于土木工程结构在服役期中的性能状况越来越关心,随之诞生的针对大型土木工程结构的健康监测理论和技术研究成为近20年来土木工程领域的研究热点[1]。对检测到的结构损伤信号分析与处理方法的研究是结构损伤识别的关键,也是目前的研究热点之一[2]。小波变换作为一种新的信号处理方法,以其在信号处理方面的强大功能,正被逐步引入到结构损伤检测中[3-5]。小波分析方法是一种窗口面积固定,但窗口形状可变(时间窗和频率窗都可改变)的时频局部方法:即在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率,很适于探测正常信号中夹带的瞬态反常现象并展示其成分[6-7]。在结构振动状态监测中,信号波形突变点往往包含反映结构状态的重要信息,因此,对信号突变点的监测具有重要意义[8]。最早使用这种方法的是AL-KHAL IDY等[9-10],他们研究了单自由度线性弹簧质量减振器模型,小波分析的结果可以准确捕捉到结构损伤发生的时刻。L IEW等首先将基于空间域响应的分析方法用于含有裂缝的结构的损伤定位[9]。他们在含有横向边缘裂缝的简支梁上沿梁长度方向施加快速移动荷载,同时采集沿梁高度方向的位移响应,然后将其作小波变换,从而得到图形上可以明显看出在裂缝位置附近的奇异点。廖锦翔等在单裂缝和双裂缝的悬臂梁上作了数值模拟,空间域信号分别为静力位移、模态位移和冲击荷载位移[12]。将信号作小波变换后根据小波系数图上的突变确定损伤的位置,效果良好。笔者利用小波变换的优点,提取应变能的损伤信号来建立结构损伤指标,数值模拟结果证实了该方法的准确性和可靠性,表明了该方法的简易性和实用性。

1 小波分析的基本原理

2 小波奇异性检测原理

如f在点t0不连续但在t0的邻域有界,则其Lipschitz指数为0。当α=0时,式(6)成为|f(t)-f(t0)|≤C,左面最多等于f在点t0的跃度,取C等于或大于跃度,则式(6)成立。还可以将Lipschitz指数推广到负数的情况,并可以清楚地看出,Lipschitz指数确实能在更一般的意义下定量地描述函数的奇异性。需注意,采用某种小波计算出来的Lipschitz指数越趋近于零,那么该小波对检测奇异信号越具有良好的效果[13]。

3 算例分析

3.1 简单悬臂梁的模拟损伤检测

采用悬臂梁进行数值模拟,以应变能的损伤信号为结构损伤指标进行结构位置损伤识别。该悬臂梁的几何和材料参数如下:L=2 m;截面尺寸b×h=300 mm×600 mm;弹性模量EX=2.06×1011Pa;密度ρ=7 800 kg/m3;泊松比为0.3。

为了模拟结构的损伤,首先将梁划分为20个单元,损伤单元为16单元,其中损伤程度(平均抗弯刚度)为刚度折损10%。

图1 悬臂梁结构模型Fig.1 Cantilever beam structuremodel

利用有限元软件ANSYS获取该悬臂梁在自由端承受10 kN静力作用下的应变能沿梁长分布,并以此作为小波分析的被处理信号来检测梁的损伤情况。

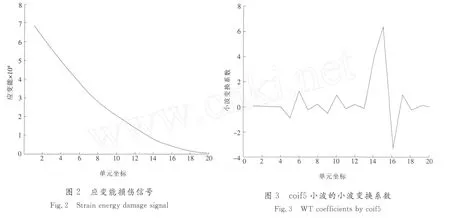
根据图2应变能损伤信号情况来看,损伤信号变化并不明显,因而无法识别损伤单元。图3对应的是coif5小波函数经过小波变换得到的小波变换系数,在损伤单元16处出现明显的峰值,根据小波分析的奇异性检测原理,出现严重奇异的位置就是结构参数变化不协调、不连续的位置,即损伤发生的位置,那么很显然,据此可以判断出来在单元16处出现损伤(与模型模拟情况吻合)。

3.2 平面钢桁架的模拟损伤检测

采用如图4所示的平面钢桁架模型,全长18 m,高2 m,两端均为铰接,并且为上弦杆支撑,上下弦杆长度均为2 m,腹杆长度为2.236 m,该桁架共有19个节点,上弦杆10个,下弦杆9个。该桁架弹性模量EX=2.06×1011Pa,泊松比为0.3,钢材密度ρ=7 800 kg/m3,杆件截面为工字型截面,规格为400 mm×400 mm×12 mm×12 mm,该桁架每根杆件分为1个单元,共有35个单元。其损伤单元为17单元,其中损伤程度(平均抗弯刚度)为刚度折损10%。

利用有限元软件ANSYS获取该桁架在节点7和节点13处承受30 kN静力作用下的应变能沿桁架分布,并以此作为小波分析的被处理信号来检测梁的损伤情况。

图5和图6对应的是结构单元17损伤的损伤信号和小波变换系数,从图5中的原始信号无法看出平面钢桁架中的损伤单元,将信号进行小波变换后如图6所示,在单元坐标为17处出现明显的峰值,根据小波分析的奇异性检测原理,出现严重奇异的位置就是结构参数变化不协调、不连续的位置,即损伤发生的位置。很显然在单元坐标为17处出现奇异点,说明17单元发生损伤,基本与假定相符合,这是离散小波分析情况。

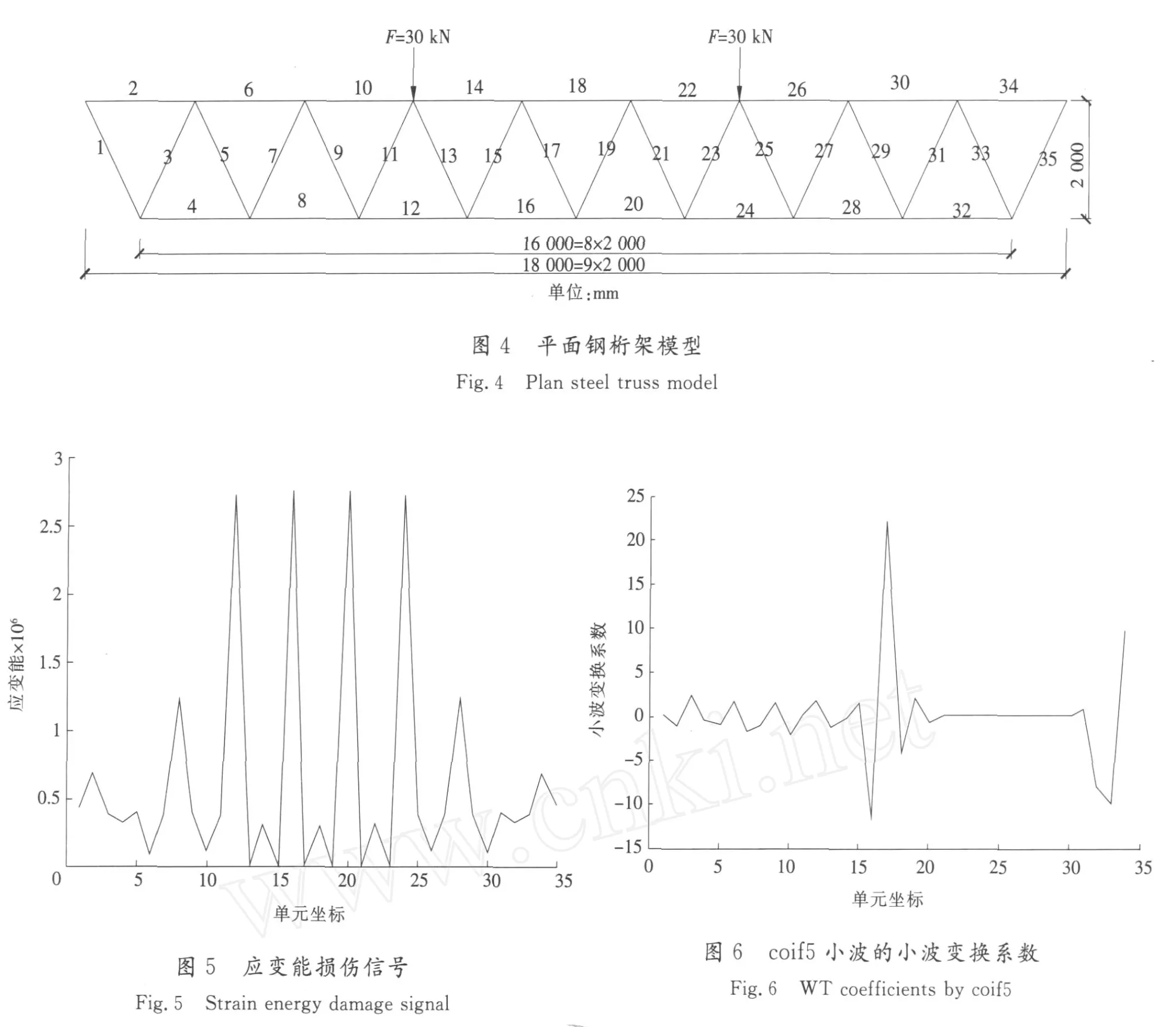
图7是损伤单元17的连续小波变换,从频谱图小尺度结果上能很清楚地发现,在损伤位置单元17附近,分析信号出现了奇异或者不连续。但随着尺度的增大,这种定位出现了偏差,这与小波分析随尺度的增大,平滑作用也增大是一致的,所以小尺度上的结果更准确可靠。

3.3 正放四角锥网架结构模拟损伤检测

如图8所示的正放四角锥空间网架结构,上平面有 36个节点,间距1 m,下平面相距0.7 m,网架材料参数是:弹性模量EX=2.06×1011Pa;泊松比 0.3;杆件面积A=50 mm2;钢材密度ρ=7 800 kg/m3。工作时网架上平面的边缘节点固定,下平面的每个节点承受垂直方向载荷10 kN。该网架每根杆件分为1个单元,共有200个单元。

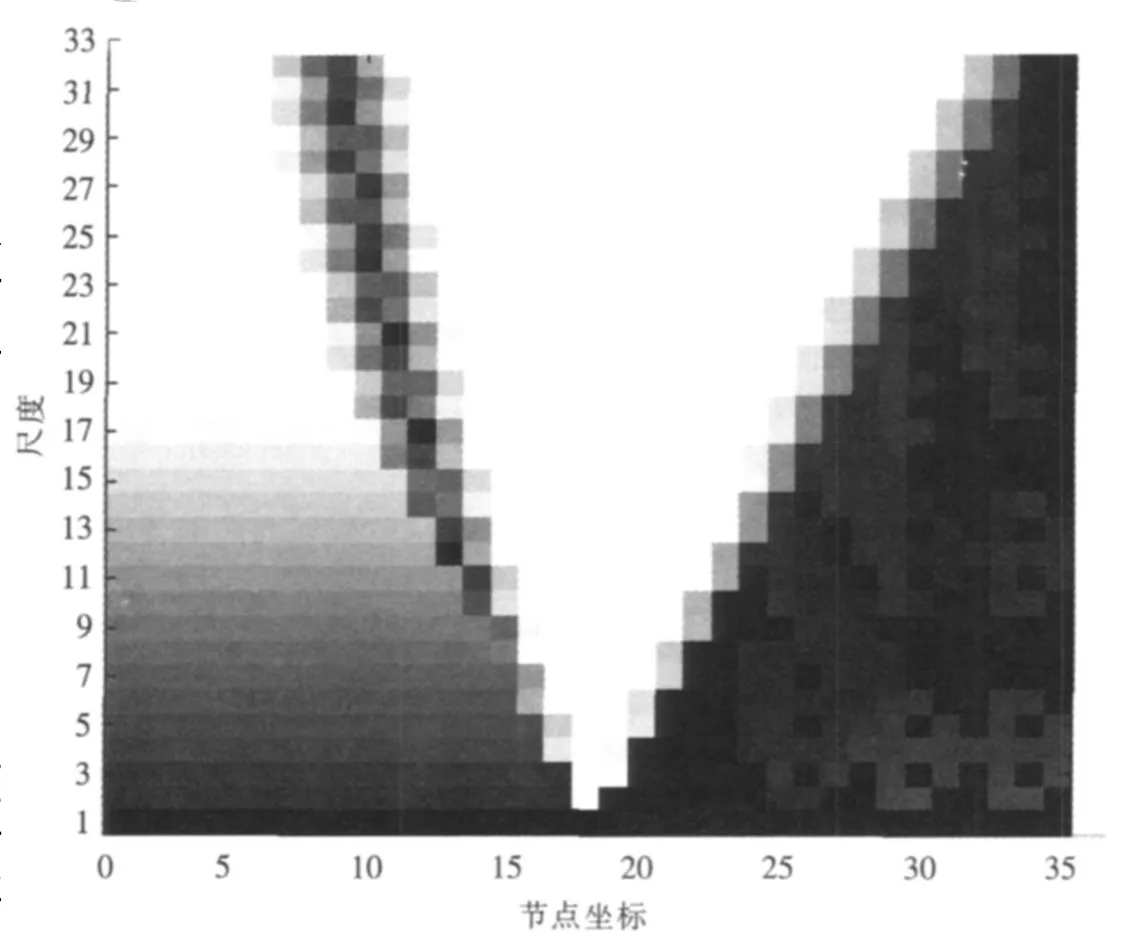
图7 应变能损伤信号的连续小波变换Fig.7 CW T of strain energy damage signal

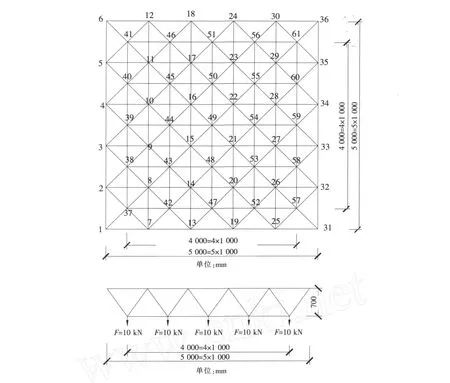
图8 正放四角锥空间网架模型Fig.8 O rthogonal pyramid space trussmodel

利用有限元软件ANSYS获取该网架在下平面的每个节点承受垂直方向载荷10 kN静力作用下的应变能沿网架分布,并以此作为小波分析的被处理信号来检测梁的损伤情况。其损伤工况见表1,其中损伤程度为平均抗弯刚度。

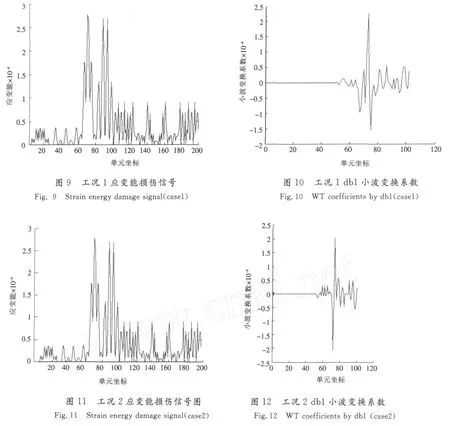
图9和图10对应的是工况1结构损伤的原始信号和小波变换系数,从图9中的原始信号无法看出正放四角锥网架结构的损伤单元,将信号进行小波变换后如图10所示,在单元坐标为70处出现明显的峰值,很显然在单元坐标为70处出现奇异点,说明70单元发生损伤(与模拟损伤情况吻合)。

图11—图13对应的是工况2结构损伤的原始信号和小波变换系数。从图12可以看到,将损伤信号进行小波变换后,在单元坐标为70处出现明显的峰值,很显然在单元坐标为70处出现奇异点,说明70单元发生损伤,从图13可以看到在单元150处出现明显奇异点,说明单元150处出现损伤,这与基本假定相符合。

表1 单元损伤情况Tab.1 Damage cases

4 结 论

根据小波奇异性检测理论,以应变能的损伤信号为结构损伤指标,分别以悬臂梁结构、平面桁架结构和空间网架结构为例进行数值模拟,将原始损伤信号和经过小波变换后的损伤信号进行对比,结果表明:

1)对已发生的损伤,小波变换只需要获得损伤结构位置参数的空间分布信号,就可以识别到损伤发生的位置或区域。

2)结构损伤折损了刚度的10%,损伤较微弱,小波分析能对结构较微弱的损伤信号进行识别,在损伤程度比较低的情况下,小波分析具有明显的优势。

3)该方法可以有效地识别结构中单一和多损伤的位置,对钢结构的检测和提高损伤定位的效率具有优越的现实意义。

[1]刘 涛,李爱群,丁幼亮.小波分析在损伤识别中的应用[J].地震工程与工程振动(Journal of Earthquake Engineering and Engineering Vibration),2008,28(2):29-35.

[2]陈长征,罗跃纲,白秉三,等.结构损伤检测与智能诊断[M].北京:科学出版社,2001.

[3]HOU Z,NOORIM,AMAND R S.Wavelet-based app roach for structural damage detection[J].J Engrg Mech,2000,126(7):677-683.

[4]SUN Z,CHANG C C.Structural damage assessment based on wavelet packet transfo rm[J].J Struct Engrg,2002,128(10):1 354-1 361.

[5]HAASE M,W IDJAJA KUSUMA J.Damage identification based on ridges and maxima lines of the w avelet transform[J].Journal of Engineering Science,2003,41:1 423-1 443.

[6]岳 猛,姜恩勇,马润杰,等.基于小波变换和CUSUM算法的PDOS攻击检测方法[J].河北科技大学学报(Journal of Hebei University of Science and Technology),2008,29(1):33-35.

[7]段培超,周春平.基于小波变换和数学形态学的航空图像边缘检测[J].河北科技大学学报(Journal of Hebei University of Science and Technology),2006,27(2):158-161.

[8]王素华,张伟林.斜拉桥斜索损伤分析中的小波变换研究[J].安徽建筑工业学院学报:自然科学版(Journalof Anhui Instituteof A rchitecture&Industry(Natural Science)),2004,12(3):13-17.

[9]AL-KHAL IDY A,NOORIM,HOU Z,et al.Healthmonitoring systemsof linear structuresusingwaveletanalysis[A].Proceedingsof International Workshop on Structural Health Monitoring:Current Status and Perspectives[C].Stanford:StanfordUniversity,1997.164-175.

[10]AL-KHAL IDY A,NOORIM,HOU Z,et al.A study of healthmonitoring systemsof linear structures usingwaveletanalysis[A].Proceedings of the 1997 ASM E PressureVessels and Piping Conference[C].FL:Orlando,1997.49-58.

[11]L IEW K M,WANG Q.App lication ofwavelet theory for crack identification in structures[J].Journal of Engineering Mechanics,1998,124(2):152-157.

[12]廖锦翔,袁明武,张劲泉.小波变换在桥梁结构损伤识别中的应用[J].公路交通科技(Journal of Highway and Transportation Research and Development),2004,21(11):30-34.

[13]王振林,聂国华.基于曲率模态和小波奇异性的结构损伤识别[J].力学季刊(Chinese Quarterly of Mechanics),2009,29(2):278-283.

App lication of wavelet singularity to steel structural damage detection

ZHANG Yue,DU Shou-jun,ZHANG Li-mei
(College of A rchitecture and Civil Engineering,Hebei University of Science and Technology,Shijiazhuang Hebei 050018,China)

The inevitable damage,aging of steel structures in use p rocess,needs detecting damage location.The wavelet analysis technique p rovides new ideasand methods for the steel structural damage detection.Based on the theory of wavelet singularity detection,w ith the injury signal of strain energy as structural damage index,and cantilever beam structure,p lane truss structure and spatial truss as examples for numerical simulation,the original damage signal and the damage signal after wavelet transformation is compared.The calculational result show s that the p resentmethod as a reliable and p racticalway can be adop ted to detect the single and several locations of damage in structures.

damage detection;damage location;wavelet singularity;strain energy;wavelet transfo rmation

U 441+.4

A

1008-1542(2010)02-0151-07

2009-09-08;

2009-11-10;责任编辑:冯 民

张 悦(1981-),女,河北石家庄人,硕士研究生,主要从事结构动力损伤检测方面的研究。

杜守军教授