浅议科学思维方法教育的紧迫性
2010-12-25连文星
连文星,连 玥
(河南教育学院数学系,河南郑州 450046)
浅议科学思维方法教育的紧迫性
连文星,连 玥
(河南教育学院数学系,河南郑州 450046)
对河南省首届女大学生就业才艺大赛笔试中的2道试题进行分析,给出正确答案,阐述思考方法,从而说明科学思维方法的重要性及落实教育部、科技部有关指示的迫切性.
教育改革;科学思维方法;开放式题型;数学模型
1 问题的提出
河南省女大学生才艺大赛中,参加大赛笔试的选手有武大、华南师大、陕西师大和郑大等国家重点大学的本科生和硕士生[1],可谓档次不低,然而面试的情况令人意外得低下.据《河南商报》报道:其中“种树题”“难倒了不少选手”,“硬是把不少选手拖到最后一分钟才交卷”;其中的“卖酒题”“更难”,不少选手干脆写“这酒我不卖了.”[2]由于影响巨大,报纸第二天便登出了结论:“这两道题没有标准答案,只要思路新颖,符合题目要求,都是正确的.”并且每题都给出了两个无任何说明的例解[3].笔者感到很吃惊,为什么选手们不去思考,不用逻辑方法推导而仅仅依靠猜测?为什么舍弃唯一正确的答案?特别是还有一个小题是伪命题,是根本不该出的题目!可组委会的答复是,专家们说:“题目都是有出处的典型题.‘种树题’和‘卖酒题’是开放式题型,各有两个解答都正确,‘剩羊题’无误,有资料可查.”——两句话不仅把正确的答案拒之门外,而且公然忽略了国家“在科技活动中要坚持科技知识、科学方法、科学态度、科学精神并重”的方针.
为什么会出现这种情况呢?原因是这些“另类题”在正规教材中没有.长期的应试教育只重视课本知识的灌输而忽略思维方法的运用,从而限制了能力的发展,学生、教师都只善于解决教材涉及的题型、题目,面对这些“另类题”,选手们只好“瞎猜”,专家只会转抄了(这类题集也是只给答案不讲方法).而实际生活中,人们遇到的问题,不管是数学的、物理的,或社会科学各方面的,绝大多数都是教材外的“另类题”,我们必须会思考、讲方法才有能力解决它们,正如爱因斯坦著名的成功公式A=x+y+z,其中y指正确的思考和方法.
2 分析
从原则上讲,创造性是现代人才思维品质的重要标准.它不仅需要丰富的知识储备,更须经过严格的科学思维方法训练.为了从源头上推进创新型国家建设,科技部于2007年专门设立了科技基础性工作专项13项,其中有一项即为“科学思维、科学方法在高等学校教学创新中的探索与实践”(编号:2007FY141100),由全国高等学校教学中心牵头承担,主要针对科学思维、科学方法在高等学校教学改革中的创新人才培养的探索与实践进行研究.全国高校都积极响应,设立了有关课题和机构,开展了相应的教学和研究.可这些也是来自高校的学生和教师为什么有如此表现呢?原因除长期的应试教育影响外,就是对此号召认识不深,执行不力,另有对开放式试题的误解.
所谓开放式试题,的确有别于填空、判断、简答等封闭式题目,由于无明确的指向性,思维的空间宽广得多,因而一定要求有更多的分析和讨论,须根据不同的情况进行对比和探究,能更好地,综合地考核被测对象的知识基础,经验能力,素质和预后发展.正因为此,开放式试题不仅在各类学校考试中越来越广泛地使用[4],在公务员招聘等各类考评中更是大量涌现并成为重要题型.开放式试题的要求和评分标准主要有:①知识性问题往往有明确的唯一性答案,且须以通用教材的内容为依据;②开放性问题须有分析过程,推理正确、归纳无误,如果有多元性结论,须加以比较并指出最优选择;③开放性问题目前尚无结论或正在研讨之中的,可以根据自己对问题的理解进行判断、想象、预测、展望,但须合情合理,不违背现实和国情,并应体现正确的价值观.
由此看来,才女大学生的“个性答案”:“分剪树苗”、“朋友合种”、“估计着倒出2两酒卖”[2]等不是“新颖的解答”而是“胡说八道”,专家组拒绝最佳结果作标准答案也是举措失当.而且,他们视为“偏”、“怪”的难题,如果用一般科学思维方法中的数学方法[5-8],难点将迎刃而解,变得极其简单而有趣.笔者给出分析和解答如下.
3 题目解答
3.1 种树题
题目 你获10株树苗,现须分种5排,每排4株,如何种植?画出示意图.
思路 种树点茫然难寻,应通过转化/化归思想,将此动性、复杂的问题转为易于把握的静态,即通过直线及其相交来确定它们.为此,特选用实验法(依题意展开,紧扣条件,实际演算或构图,随时校正).步骤如下:
(1)如图1,任划一直线a,在上面暂定植树点A、B、C、D.
(2)由于5×4=20>10知种树点应同时处在不同的排,即在交点上,故应过a上树点,如A作直线b并暂定树点E、F、G.
(3)同理,在a、b上各选一树点,不妨C、F连线为直线c(不可再任意选树点).
(4)在a、b上另选一对树点,不妨为B、E连线d交c于树点H.
连a、b最后一对树点D、G,而得直线e,选与c、d的交点J、I为树点.至此,树点集{A,B,C,D,E,F,G,H,I,J}恰符合条件:分居5排且每排4株.
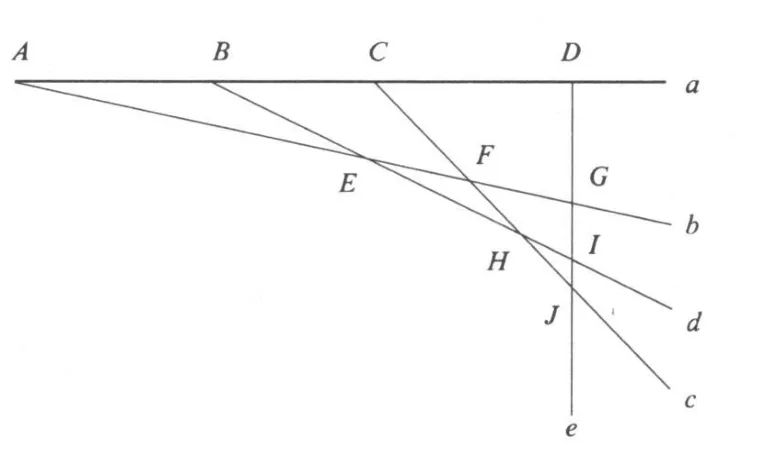
图1 种树题解题思路
分析 ①前7个树点和后3对树点都有“随意性”,连线有可能“难相交”,不妨另选树点.②选点不同对应不同做法,计有C·C·C·C·C=144种,无必要逐一成图.③为举例,随意施以不同做法即可得图案如图2(不少种做法成图类似,余若干类略).④应考虑成图美观、地面节约、易于施植和管理等因素,144种方法所成若干类图形中,当以中心对称的正五星形之十个顶点因三个特点而最优:所圈面积最小、位置最均衡、等长线段最多.
实解 实际种植远较纸上作图难,不仅无法画“特大圆”,也不易通过圆再画出正五星形而后确定10个植树点.应直接定点施植(这也正是知识、能力的考查点).步骤如下(有关计算从略):
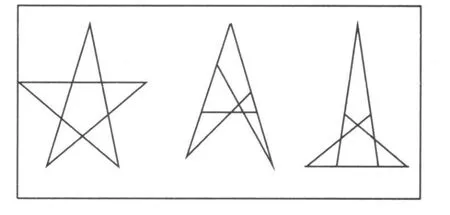
图2 种树题的其他解法
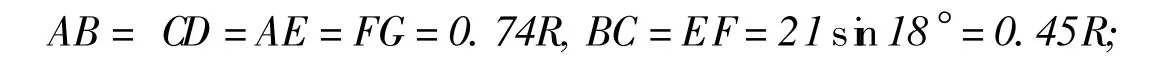
(3)双向外延BE至H、I,使BH=EI=0.74R,取H,I为树点;
(4)延长AO至J使H、C、J、G共线(I、F、J、D也共线),取J为树点.至此,点集{A,B,C,D,E,F,G,H,I,J}为植树点的最优选择.
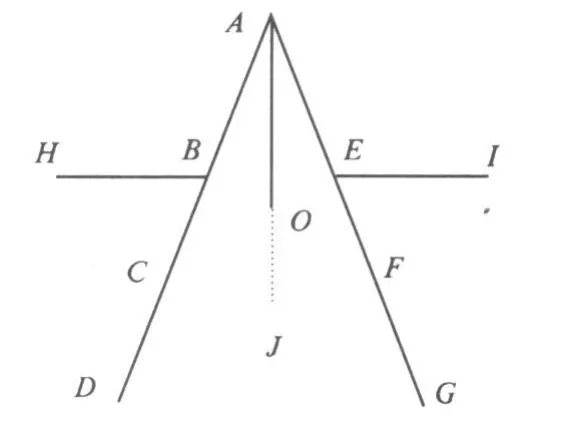
图3 种树题实解图
3.2 卖酒题
题目 仅有7两、11两舀勺,如何倒出2两酒卖出?写出过程.
思路 为了将实际现象描述得更具科学性、逻辑性、可重复性,最好的方法就是用数学语言来表达.所以,笔者通过转化—建模思想,利用数学模型法给出解答:
(1)舀、倒的行为体现了加减法,勺的种类限定了算式的生成数字仅7及11,多次施舀对应其不同倍数,因而须考查以下数列:
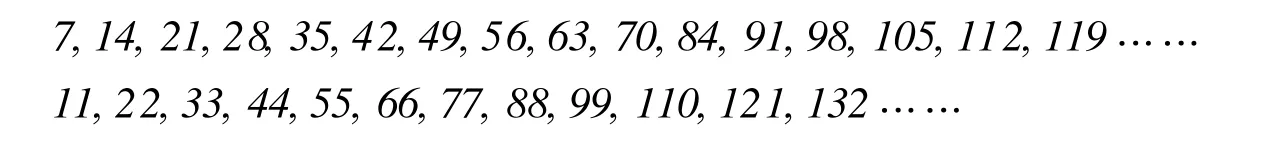
(2)“卖出2两酒”表明算式得数为2,比照数列表上最小的异行差便得基本算式为35-33=2.
(3)舀酒进勺相当于“加上”,倒出勺相当于减去,基本算式对应最简算式7+7-11+7+7-11+7-11.
(4)为了更容易看出操作过程,可以转化为过程分解式如图4.
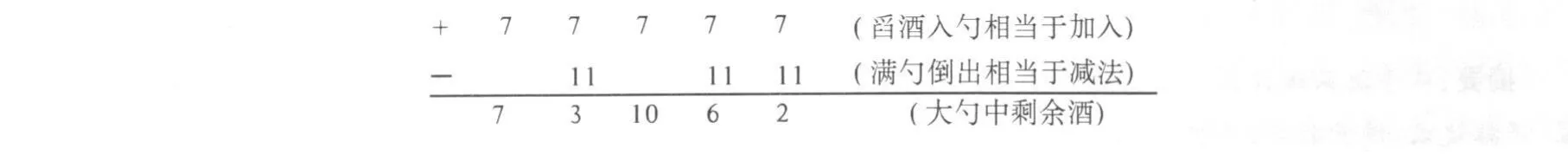
图4 卖酒题的分解式
实际操作 舀满7两倒入大勺,再舀7两倒入时剩3两,将大勺腾空后倒入,再连舀7两两次倒入大勺时,后次只能倒入1两而剩6两,仍将大勺腾空倒入,第五次舀7两倒入大勺时仅能倒入5两而余2两,恰可卖出.
评议 ①如果将舀入或倒出一次算一步,则上述操作仅需8步(MD=3);②专家组给出二法相当于取基本算式为44-42=2,(22-21)×2=2,相应步数为10步、11步.另外,还可取121-119=2,(56-55)× 2=2……为基本算式,操作步骤将更复杂;此题解法可能无穷多,同类题目也有很多,如增设舀勺或改变要求.但是只要掌握此法都极易作出.
显然,这两个题的解法涉及的知识仅有“平面上二直线相交”和“八个个位数的加或减”,从而使我们看到了思维的力量和方法的奇效,能使“迂回无路”时乍见“柳暗花明又一村”了.
至于大赛笔试中的小“逻辑题”:农夫有17只羊,除9只外都病死了,问农夫还剩几只羊?答案是9只.专家很叫好,说“设了逻辑陷阱,可考验选手受否‘白马非马’典故的影响”,但笔者并不认同此观点.原因有两点:①本题中条件“除9只外都病死了”,其意实同于“病死后尚有9只”——已知还剩9只,命题者明知故问,反映的只是伪命题;②“白马非马”之辩自古以来皆因“非”的含义而争论不止,后来有人从逻辑的辩证分析其意义也并未肯定其为真命题,从而不会有选手由此推论.即使错答为17,也只是出于逆反、投机心理而已.
4 结论
以上问题是数学试题,所以我们运用数学思想和数学方法来解决(也并非单一的数学方法解决的,常要互补联用,因而应提升至逻辑思维方法中的思维变换和计算推理、归纳推理).实际上人们遇到的问题来自实际生活的各个方面,这就需要我们从宏观上,即科学思维方法上考虑教育的改革和发展问题,切实加强科学思维方法教育,进一步开展有关课题的研发活动,掀起教学改革的新高潮.
[1] 李肖肖,訾利利.河南首届女大学生就业才艺大赛前100名名单[N].河南商报,2010-01-20(A07).
[2] 李肖肖,訾利利.才女大赛首场PK考女生价值观看看才女们都给出了什么答案[N].河南商报,2010-01-18(A07).
[3] 李肖肖,訾利利.“种树题”你做出来了吗[N].河南商报,2010-01-19(A08).
[4] 但纯.复旦的“刁钻”考题是有意的尝试[N].大河报,2010-02-09(A24).
[5] 刘冠军,王维先.科学思维方法论[M].济南:山东人民出版社,2000.
[6] 张大松.科学思维的艺术·科学思维方法导论[M].北京:科学出版社,2008.
[7] 刘凤瑞.教育科学的新思维[M].北京:中国大地出版社,2007.
[8] 吴先金,程德兴.对创新思维教学法的一些探讨[J].江汉石油学院学报:社会科学版,2000,2(1):46-48.
On Urgency ofEducation of ScientificThinkingM ethods
L IAN W en-xing,L IAN Yue
(Depar tment ofM athematics,H enan Institute of Education,Zhengzhou 450046,China)
Analysis on two questions in writing exam ination of employm ent talents for female college students in H enan province,presents correct answers andmethods of consideration to show the importance of scientific thinking method and the urgency of practice the direction ofAdm inistration of Education andM inistry of Science and Technology.
refor m of education;methods of scientific thinking;open-ended;mathe m aticalmodel
G642.0
A
1007-0834(2010)02-0063-03
do:i 10.3969/.j issn/1007-0834.2010.02.021
2010-03-22
河南省教科“十一五”规划项目(2008-J KGHAGH-271)
连文星(1940—),男,河南禹州人,河南教育学院数学系教授,主要研究方向:计算数学、数学逻辑.
