单缝夫琅禾费衍射实验的计算机辅助教学

何 杰,宋立涛

(1.河南工业大学,河南郑州 450001;2.郑州大学,河南郑州 450052)

单缝夫琅禾费衍射实验的计算机辅助教学

何 杰1,宋立涛2

(1.河南工业大学,河南郑州 450001;2.郑州大学,河南郑州 450052)

传统的衍射实验往往过多强调光波波动性的一面,而忽略其粒子性的一面,从而使学生对衍射现象的物理过程缺乏全面的认识。在进行光学实验的同时,借助于计算机辅助教学,可弥补这一缺点。应用蒙特卡罗方法对单缝夫琅禾费衍射现象进行了模拟,对模拟结果进行了分析和讨论。与传统方法相比,这种方法更为形象和直观,可以帮助学生理解光子等微观粒子的波粒二象性及随机性与确定性的统一。

衍射;蒙特卡罗;模拟;波粒二象性

理论和实验均表明,光波同时具有波动性和粒子性。干涉和衍射现象,是波动性的体现,也是粒子性的必然结果。传统的实验教学,对干涉和衍射现象的讨论,往往过多的强调其波动性的一面,而忽略其粒子性的一面,从而使学生对干涉和衍射现象的物理过程没有一个全面的认识。

光波在微观上是由光子组成的。微观粒子的描述要用量子力学,量子力学已经成为众多自然科学研究和发展的基础。让学生在做实验的同时,了解一些关于量子力学的基本概念和一些基本过程的微观物理图像,是非常重要的。量子力学中,坐标和动量的乘积满足海森伯测不准关系,不能同时确定;对微观粒子行为,用波函数Ψ描述。|Ψ|2对应的是粒子出现的几率,所以对单个光子来讲,其行为具有随机性。但实际上,光波发生干涉或衍射后,光强有确定的分布,这种确定性可以通过实验来观察,比如单缝衍射实验,而微观过程的随机性很难在实验上进行直接的观察。为了直观的理解这种微观过程和宏观现象的统一,可借助蒙特卡罗方法利用计算机对这种微观过程进行模拟。在模拟中,光子数足够多时,应该再现与经典波动理论相同的结果。

同时,随着计算机科学的飞速发展,计算机技术以及相关的计算方法已经成为现代物理学,尤其是理论物理发展的基本工具。计算机数值计算和模拟技术已经渗透到物理学的各个领域。借助于计算机这个强大的工具,许多以往不能或很难研究的系统,得到了很好的研究。在物理教学中有意识渗透一些与数值计算相关的内容已经显得非常必要。在大学物理实验教学中,利用计算机对涉及到的自然现象和规律的演示、模拟和仿真,不仅可以改进课堂教学内容和方式,还可以在实验教学的基础上帮助学生进一步理解隐藏在现象背后的物理本质。

本文采用蒙特卡罗方法对单缝夫琅禾费衍射实验进行了模拟。在单缝衍射实验的基础上结合衍射过程的蒙特卡罗模拟,可以加深学生对波粒二象性这一重要概念的理解,使学生比较直观的认识到个体行为的随机性和整体行为的统计规律性的统一。这种方法易于推广到其他干涉和衍射过程,也适用于其他微观粒子,如电子。

1 单缝夫琅禾费衍射的光强分布公式

单缝夫琅禾费衍射的光强分布公式的推导可采用积分法[1]、振幅矢量图解法[2]、傅立叶变换法和级数法等。这些方法都只强调了问题的一个侧面,即波动性。为了更深入的理解包含在其中的物理本质,在做单缝衍射实验的同时,可以结合蒙特卡罗方法对光子通过单缝后的随机过程进行数值模拟。

图1是单缝夫琅禾费衍射的示意图,当衍射角为Φ时,由常规积分法或振幅矢量法可求得P点的振幅式中sinΦ。其中a为缝宽。本文只进行一

般意义上的讨论,不涉及缝宽a和入射波长λ的具体取值,而直接以α为自变量。实际应用中,当a和λ给定后,由α的取值可计算出对应的衍射角Φ。

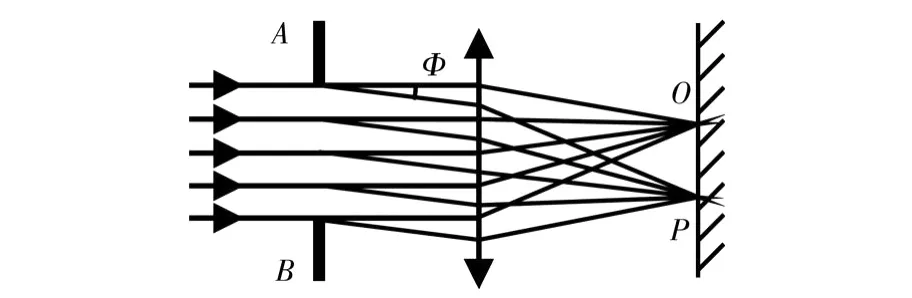
图1 夫琅禾费单缝衍射示意图

2 用蒙特卡罗方法模拟单缝夫琅禾费衍射

蒙特卡罗方法也称随机模拟法,是一种基于“随机数”的计算方法,其应用非常广泛。应用这种方法,针对公式(1)可采用下述方案在观测屏上得到衍射图样:首先应用Mersenne twister方法产生伪随机数序列,然后用舍选抽样法[3]选取N个在x方向按式(1)分布、y方向均匀分布的二维随机数,用以模拟打在屏上的光子。单个光子在穿过狭缝后,行为具有随机性,事先不能确定其运动方向,只能知道其沿各个方向运动的概率。模拟中,可以选取N取不同的数值,在衍射屏上得到不同入射微观粒子数的衍射图样。当光子数足够多时,应该再现与经典波动理论相同的结果。从而帮助学生理解衍射过程中,光的波动性和粒子性是如何统一起来的。

3 结 论

图2给出了由理论公式得到的光强分布和衍射图样,其中2(a)是衍射图样,2(b)为光强分布曲线。图3给出了入射光子数N取不同值时由蒙特卡罗方法模拟得到的光波衍射图样。图中的每一个点代表一个光子,(a),(b),(c),(d)四个衍射图样的入射光子数分别为27,250,2311,23676。比较可以发现,图3(a)由于入射的光子数很少,光子在衍射屏上的分布近似随机,无规律可言;图3(b)已能看出光子入射到中间的几率大于两边;图3(c)已能看出衍射图样的形状;图3(d)由于入射光子数较多,衍射图样和理论分布趋于一致。进一步增加入射的光子数,模拟结果表明,光子数非常多时得到的结果和图2(a)完全一致。

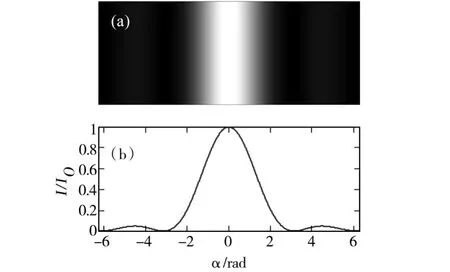
图2 由理论公式得到的光强分布和衍射图样

图3 N取不同值的衍射图样

图4是用matlab语言编制的一个图形界面程序的截图,学生只需输入几个模拟参量,就可以利用蒙特卡罗方法对单缝衍射实验的微观过程进行模拟并查看结果。学生在对单缝衍射实验进行实际操作和分析后,将对光波的波动性有一定感性认识,然后借助于类似的小程序,就可以进一步了解光波的粒子性,从而使学生对光波的波粒二象性有一个比较全面的认识。综上所述,模拟过程很好的展示了单光子行为的随机性和大量光子行为的统计规律性,结合单缝夫琅禾费衍射实验,可以使学生更为形象直观的理解光波的波粒二象性以及确定性和随机性的辩证统一。

图4 图形界面程序

[1]赵凯华,钟锡华.光学:上册[M].北京:北京大学出版社,1984:78.

[2]刘克哲,张承琚.物理学:下卷[M].北京:高等教育出版社,2005:98-99.

[3]方再根.计算机模拟和蒙特卡罗方法[M].北京:北京工业学院出版社,1988:125.

Computer-aided Instruction of Single Slit Diffraction

HE Jie1,SONG Li-tao2

(1.Henan University of Technology,Zhengzhou 450001;2.Zhengzhou University,Zhengzhou 450052)

The wave character has been emphasized more than particle character in traditional experiment course of diffraction.As a result,the students could not comprehend diffraction fully.Computeraimed instruction can compensate for the defect.Single slit diffraction was simulated based on Monte CarlOMethod.The results were discussed.Comparison with traditional methods it is more visualized.It can help students comprehend the meaning of wave-particle dualism and catch on the unification of randomization and determinacy.

diffraction;Monte Carlo;simulation;wave-particle dualism

O43

A

1007-2934(2010)06-0069-03

2010-05-27

河南工业大学引进人才专项基金资助项目(2007BS041)