具有辅助性服务的多级适应性MX/G/1休假排队

贾松芳

（重庆三峡学院数学与计算机科学学院，重庆万州 404100）

1 引 言

关于M/G/1排队的许多研究成果推动了电话通讯系统、计算机和管理工程的迅速发展.近年来王成全[1]、王晓春[2]、陈佩树[3]、朱仁祥[4]、Madan[5]和 Ke[6]利用微分方程或补充变量法对可继续和辅助性服务的M/G/1排队做了更深入的研究.基于此，本文将用嵌入Markov链的方法讨论具有辅助性服务的多级适应性 MX/G /1休假排队.此模型在现实生活中例如汽车修理厂，汽车随机到达汽车修理厂，到达后修理工通常对汽车做基本的护理（如清洗），但有些汽车需换轮胎，屏风，灯或替换电池组等，在之前修理工检修修理工具和修理后把修理工具放到一定的位置做准备.

2 模型描述和嵌入马尔可夫链

具有辅助性服务的多级适应 MX/G /1休假排队策略为：一旦系统空出，服务员根据所从事的辅助工作量，要求进行H次休假，相继的每次休假时间Vk，k=1,2,…，都是独立同分布的.若在这H次休假内仍无顾客到达，结束第H次休假后服务员进入通常的闲期，闲期内批量到达的顾客均进入系统.一旦有顾客进入系统，则系统开始经历一个随机长度U的启动时间；如果对自然数 k （1≤ k≤H ），在第k次休假内已有顾客进入系统，休假期在第k次休假结束时提前终止，并经历一随机长度为U的启动时间，在休假期、启动期及服务期批量到达的顾客均进入系统，启动期结束后开始为顾客服务，服务台提供基本服务和辅助性服务.（i）假设顾客的基本服务时间为S0，分布函数 S0（t），其LST：（t），均值s0.（ii）一旦顾客的基本服务完成，顾客以概率ri要求类型i（i= 1,2,… J ）的服务，并且服务类型i立刻开始，或者以概率r0离开系统，随后队前的那位顾客将完成基本服务，且假设服务类型i（i= 1,2,… J）的服务时间Si，分布函数 Si（t），LST：（t），均值si.且服务时间内要求顾客完成一服务循环.

令AI=｛忙 期第一个顾客在空闲状态进入系统｝ Av=｛忙 期第一个顾客在休假状态进入系统｝

这里 An+1是第n+1个顾客服务时间内到达的顾客数，其中｛An,n = 1,2…｝ 是独立同分布的随机序列.而α是忙期开始时的顾客数.则服务期有k（k≥1）个顾客的概率分布和母函数分别记为：

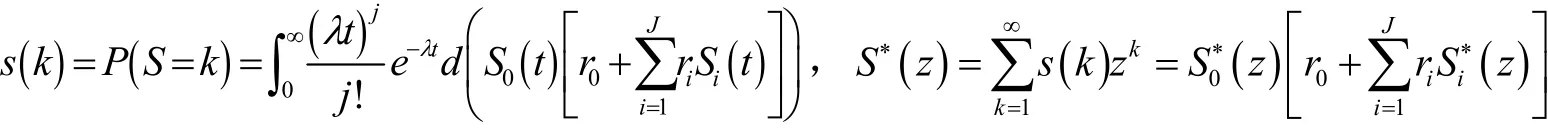
由于顾客批量到达服从复合泊松分布.一个服务期内到达A个顾客数的概率和母函数为：

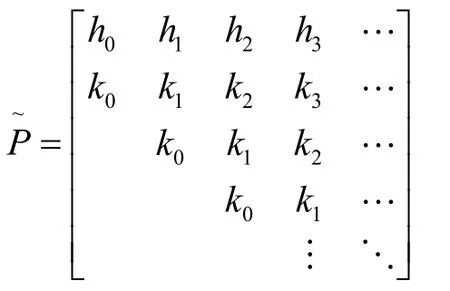
由Foster法则，可以证明，马尔可夫链｛Ln,n≥ 1｝正常返，当且仅当 ρ=λg s＜1.

3 稳态队长和等待时间的随机分解

定理 1 若ρ＜1，稳态队长Π分解成两个随机变量的和 Π=Π0+Πd，其中Π0表示辅助性服务MX/G /1排队模型的稳态队长，其LST在文献[6]中已给出，附加队长为：

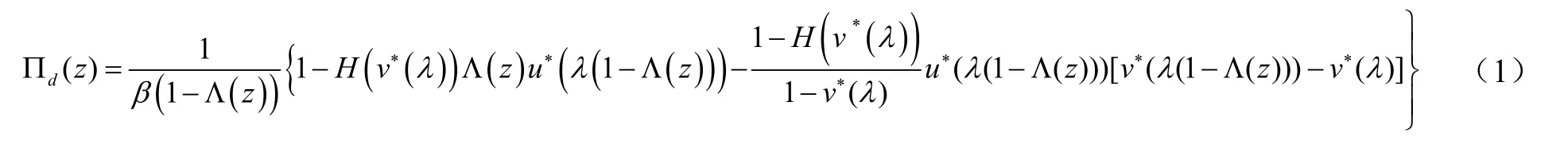
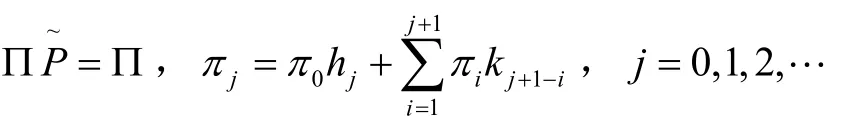
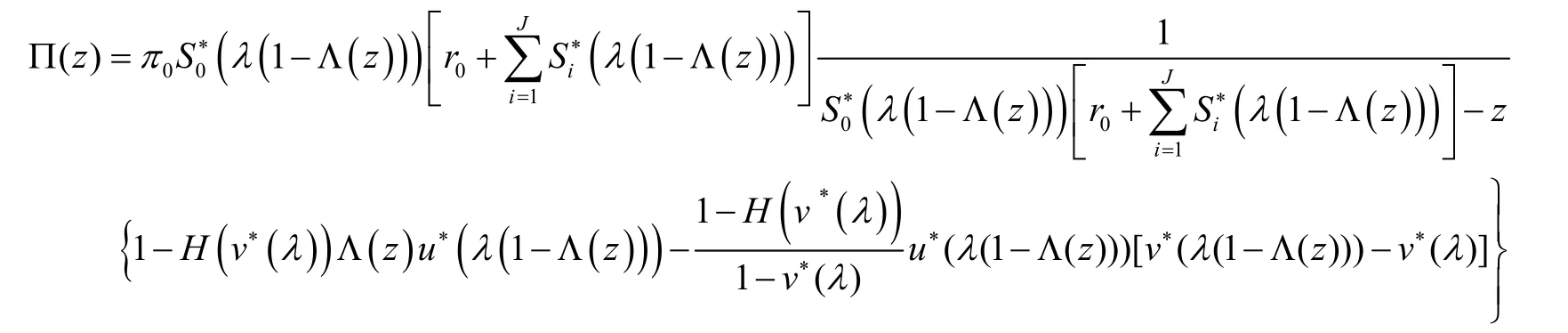
由正规化条件下Π(1)=1和 L'Hospital 法则，得 π0= (1 - ρ)β-1.将之代入上式得：

由式(3)给出了式(1)和Π0(z).则附加队长∏d的均值为：

定理 2 若ρ＜1，稳态等待时间W可分解成两个随机变量的和，即 W=W0+Wd，W0表示辅助性服务 MX/G /1排队模型的稳态队长，其LST在文献[6]中已给出，附加延迟Wd的LST为：

证明：假设在同一时刻到达的批量顾客看成一个超级顾客，那么超级顾客在M/G/1排队系统的各项指标用下标为g加以区别 MX/G /1排队系统的各项指标.由于考虑在等待顾客是随机选择的，所以顾客在系统中的等待时间由两部分时间独立组成.一是逗留顾客属于超级顾客的（这超级顾客还没有接受服务）的等待时间Wg，它的LST用（θ）表示；另一个是逗留顾客在超级顾客服务内的等待时间D，它的LST用 D*（θ）表示.一个超级顾客服务时间的概率和母函数为：

由式（3），相应 MX/G /1排队系统中一个超级顾客的服务完后系统中超级顾客数的母函数为：

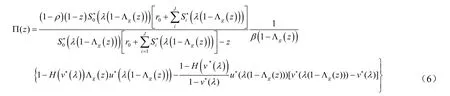
在等待时间独立于到达时刻以后的输入过程中，离去时留在系统中的顾客数，仍然等于它的等待时间W和服务时间S内到达的顾客数之和.由泊松到达过程的独立增量性质，等待时间与服务时间内到达的顾客数相互独立.

把式（5）和式（6）代入式（7），并令 λ（1- Λg（z ））=θ，则可得：

用“离散时间形式”的更新理论的一个结果求 D*（θ），如果在超级顾客中的一个逗留顾客之前假定的顾客数为Λ-，这里用到更新过程，两个连续更新点间隔为批量长Λ.而Λ-的概率分布和母函数分别（见文献[8]，第2.1节）：

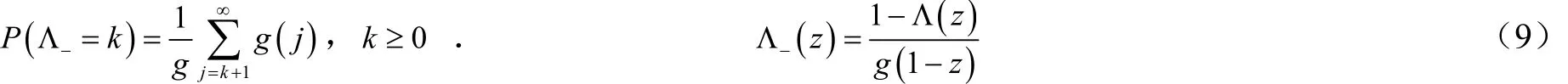
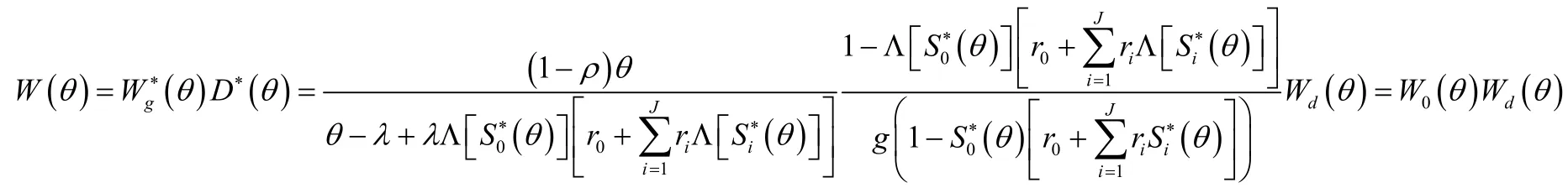
比较定理1和定理2，可得 E （Πd）= λgE(Wd)，且Little 公式成立.

4 假期循环，忙期，忙循环分析

假设 B0（θ）和（θ）为辅助性服务 MX/G /1休假排队的忙期和LST.单个顾客服务时间为 S*（θ），由Takagi[9]，顾客忙期开始时的LST为：则假设 Bv（θ），（θ）为具有辅助性服务的多级适应 MX/G /1休假排队的忙期及其LST，当无顾客到达时，关闭服务台，当至少有一顾客到达时，服务台立即开启但并未服务.在开始服务之前需一随机长度U的启动期.启动期结束，服务台开始服务.任意忙期结束时为系统的再生点，如果系统忙期开始时有k位顾客在等待，紧接的服务期包括k个相互独立的服务期，则

其中E(Bv)的（θ）均值.

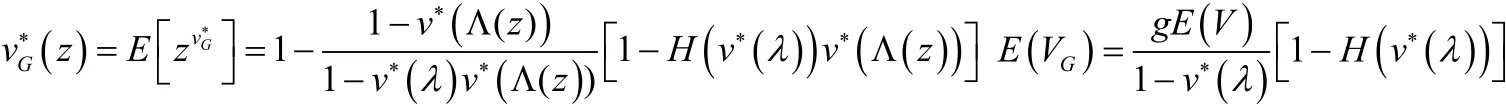
由于服务员也可能处在通常的空闲状态，若休假期间又进入，其后处于空闲状态的时间为零；若休假时间内无进入，服务员处于空闲状态的长度是一个到达间隔.以Iv表示服务员每次在空闲状态上的逗留时

在稳态条件下，记 PB,PV,PI,PU分别为系统在任意时刻服务台处于忙期，假期，空闲期和启动期的各状态概率，应用更新酬劳定理，则有

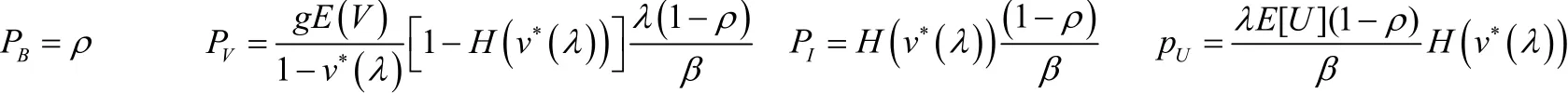
5 特 例

例如带启动时间的J种辅助性服务 MX/G /1排队.

具有辅助性服务多级适应性休假 MX/G /1排队中，当H=∞， H（z）= 0，V=0时

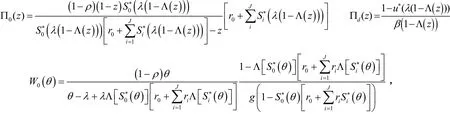
从以上特例的具体指标的结果可以看到，对于具有辅助性服务的多级适应性 MX/G /1休假排队和它的特例，验证了本模型的可行性和正确性.同时辅助性服务的多级适应性 MX/G /1休假排队中，当批到达只有一个顾客， Λ （z）= z时，系统变为具有辅助性服务的多级适应性M/G/1休假排队.

[1]王成全，朱翼隽.具有第二次可选服务的带反馈的 N一策略 MX/G /1(E，MV)排队系统分析[J].运筹与管理，2006，15（6）:91-96.

[2]王晓春，朱翼隽，陈燕.具有可选服务、反馈、一般重试时间的M/G/1排队系统[J].运筹与管理，2006，15（6）:54-59.

[3]陈佩树，朱翼隽，王晓春.有两个服务阶段、反馈、强占型的M/G/1重试排队[J].运筹学学报，2006，10（4）:71-80.

[4]朱仁祥，朱翼隽，方基奎.重试、反馈 M/M /s/k排队的呼叫中心性能分析[J].系统工程学报，2006，21（6）:613-620.

[5]Madan K.C.，Al-Nasser A.D.On MX/G,G ）/1 queue with optional re-service[J].Applied Mathematics 2 and Computation ，2004，152:71-88.

[6]Ke J.C. An MX/G /1 system with startup server and J additional potions for service[J]. Appl.Math.Model，2007:1-16.

[7]高娃，斯琴.带启动时间的多重休假 MX/G /1排队[J].运筹与管理，2006，15（2）:37-40.

[8]Cooper R. Introduction to Queueing Theory( Second edition)[M].North-Holland Publishing Company，1981.

[9]Takagi H.Queueing Analysis:A Foundation of Performance Evaluation，Vacation and Priority Systems[M].Part I，vol.1，North Holland，Amsterdam，1991.