当阳市水稻产量与气候变化的相关分析

2010-12-22刘仁进唐大清孙卫国

中低纬山地气象 2010年2期

关键词：距平时间尺度负相关

张明,刘仁进,唐大清,孙卫国

(1.湖北省宜昌当阳市气象局,湖北宜昌 444100;2.江苏省南京信息工程大学应用气象学院,江苏南京 210044)

当阳市水稻产量与气候变化的相关分析

张明1,刘仁进1,唐大清1,孙卫国2

(1.湖北省宜昌当阳市气象局,湖北宜昌 444100;2.江苏省南京信息工程大学应用气象学院,江苏南京 210044)

根据 1959-1998年当阳市的日平均气温、日降水量以及同期水稻产量资料,采用 morlet复值小波变换与小波功率谱方法,分析了近 40a来当阳市水稻气候产量、降水量以及气温的多时间尺度的时频特征,并采用交叉小波方法探讨了气候产量与降水量、气温的相关。研究结果表明：水稻气候产量与降水量均具有 5a以及 2-4a的显著周期变化,与气温均存在 2-4a的显著周期变化,而且气候产量与降水量、气温在时域分布上也存在着某些相似性特征;气候产量与降水量、气温存在着密切的相关,相关关系随振荡周期尺度的不同而不同,且气候产量与降水量在 5a和 9a时间尺度上的相关程度最大,与气温在11a时间尺度的相关程度最大;气候产量与降水量在 2～4a、6～10a、11a以及 16～20a时间尺度上呈负相关而在准 5a时间尺度上呈正相关,与气温在 2～4a、6～8a、10～12a以及 16～20a时间尺度上呈正相关而在准 5a以及 9a时间尺度上呈负相关。

水稻;气候产量;气候变化;小波

1 引言

目前,有关气候变化对作物产量的影响以及各种气象因子与作物产量的关系的研究较多,在影响我国作物产量变化的众因素中,气温和降水量是影响作物产量的主要因素[1-7]。然而,以往研究作物产量与气象因子之间的相关性时,多集中于短周期、单时间尺度的研究,研究方法多局限于多元回归、积分回归等传统的统计分析,对气候波动与水稻产量波动之间的相关进行多时间尺度分析的研究较少。小波分析在时域与频域上都具有良好局部化、多层次和多分辨的性质,从而把分析重点聚焦到任意的细节,为研究气候波动以及作物产量波动的多尺度规律与特征在不同时间尺度上的精细结构提供了良好的条件[8]。

本文选取 1959-1998年当阳市的水稻平均产量以及同期当阳气象站的日平均气温和日降水量资料,采用 morlet复值小波变换方法对近 40 a来当阳市水稻气候产量、气温年距平以及降水量年距平的时频变化特征进行多时间尺度分析,得到水稻产量变化周期与气候因子变化周期的相似性。进而采用交叉小波变换方法分析了当阳市降水量和气温的变化对水稻气候产量的影响,讨论了水稻气候产量与降水量、气温之间的相关。

2 资料处理与方法

2.1 资料处理

影响作物产量的因素可以划分成社会生产条件和气候因素两大类。为了分析作物产量与气象条件之间的关系,通常从逐年实际产量中,去掉气候因素以外的所有非自然与自然因素对产量影响的总和,这部分产量称为时间趋势产量,余下的即是受气候因素影响而变动的产量,称为气候产量[9]。二者相互关系可用数学方程式表示如下：

Ym为气候产量,Y为实际产量,Yt为趋势产量。

目前,有关求解趋势产量的方法的研究较多,主要有加权平均回归法、直线滑动均值法和指数平滑法[10-12]等。为了确立气候变化与水稻产量的相关,在采用小波变换分析之前,根据资料中的水稻实际产量序列,采用直线滑动均值法[11]求得趋势产量,进而利用 (1)式求得水稻的气候产量。为了使资料序列满足平稳随机过程的性质[13],在实际计算时,对气候产量、降水量年距平和气温年距平序列进行标准化处理,并以此序列进行时频特征分析和相关性讨论。

2.2 小波分析方法

小波函数的定义[14-16]：设φ(ω)为 1平方可积函数,即φ(t)∈L2(R),若其傅立叶变换Ψ (ω)满足容许条件：

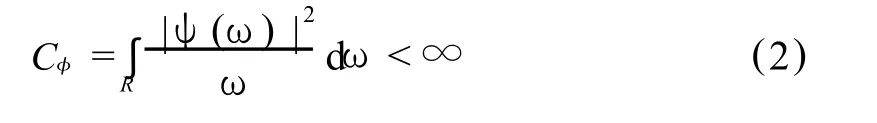
则φ(t)称为一个基本小波或小波母函数。将小波函数φ(t)进行伸缩和平移,得到连续小波：

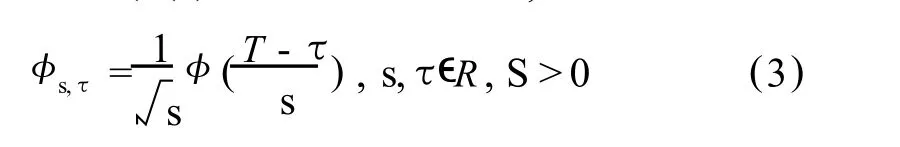
小波变换将信号分解在不同的时频尺度上,时间函数 f(t)的连续小波变换可表示为[13]：

其中,s为伸缩尺度,τ为平移参数;函数ψ(s,t)=|s|φ(t)由母小波φ(t)定义,本文选用 Morlet小波。

小波能量谱的概念与频谱的概念相类似。小波功率谱定义为[17]：

将红噪声功率谱假设检验方法应用于小波功率谱[13],采用小波功率谱与其红噪声总体谱的比值可以检验给定信度条件下小波功率谱的显著性水平。

对于两个平稳随机过程,根据相关系数的定义,小波互相关系数可表示为[13]：

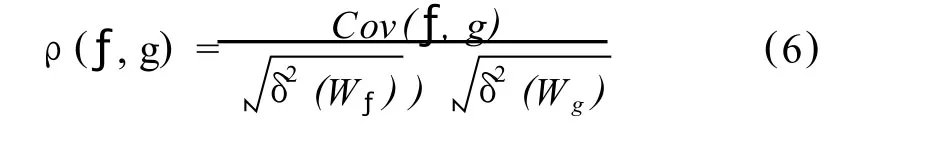
上式中,Cov表示方差。小波互相关系数可以反映时间函数 f(t),g(t)经过小波变换后在时间域和频率域中的互相关程度随振荡频率和时间后延的变化,由此可分析两者相关振荡的时频结构特征。

3 结果分析

3.1 水稻产量和气候因子在不同频域中的时间变化特征

小波分析的目的是从原始数据中提取不同特征时间尺度的周期信息。这里采用morlet复值小波来分析当阳市水稻气候产量、降水量年距平以及气温年距平的特征时间尺度和周期性特征。通过对序列进行morlet复值小波的连续变换,可以得到小波变换系数的实部信息,通过分析这些信息,能够揭示变量的多时间尺度结构[8]。

图 1是对当阳市 1959-1998年水稻气候产量以及降水量与气温年距平做Morlet小波变换得到的小波系数实部等值线图。小波系数为正时,表示水稻气候产量或降水量年距平或气温年距平相对偏多,图中用实线表示;小波系数为负时,表示相对偏少,用虚线表示;小波系数为 0的地方则为突变点。图中的符号反映了振荡的位相,等值线中心反映了不同尺度振荡的振幅最大值。

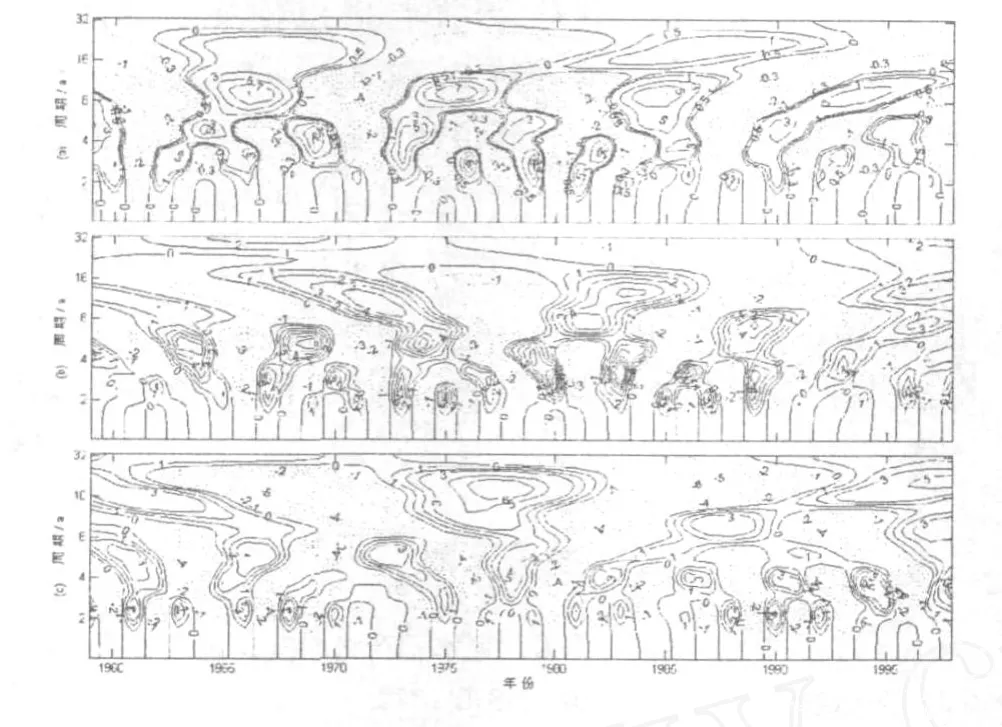
图 1 气候产量 (a)、降水 (b)与气温年距平(c)的Morlet小波系数实部等值线图

从对Morlet小波变换系数实部的分析可知,气候产量与降水量和气温变化存在不同尺度的周期变化,但两两之间的振荡变化存在着极大的相似性。对比图 1(a)(b)可知,气候产量和降水量都存在 2-4 a以及准 5 a时间尺度的振荡;对比图 1(a)(c)可知,气候产量和气温都存在 10 a以及 20 a时间尺度的振荡。这说明在不同时间尺度上气候产量与降水量和气温存在一定的相关关系。

图 2 气候产量 (a)以及降水 (b)、气温年距平(c)的小波功率谱显著性检验

3.2 水稻产量和气候因子变化的显著周期

图 2给出了气候产量、降水量年距平以及气温年距平的小波功率谱显著性检验。图 2中等值线数值为气候产量、降水量年距平以及气温年距平的小波功率谱与置信水平为 95%的红噪声总体谱的比值,比值＞1.0表示通过信度检验的显著周期振荡(实线),比值＜1.0表示未通过 95%置信水平的红噪声检验 (虚线)。

通过小波功率谱分析发现气候产量,降水量年距平和气温年距平变化的时频结构分布具有一定相似性,表现为在频率域上气候产量与降水量都存在 5 a左右以及 2～4 a的显著周期变化,与气温都存在 2-4 a的显著周期变化,而且在时间域中的分布两两之间都具有明显的局部变化特征。对比图 2(a)(b)可知,在 2～4 a时间尺度下,水稻产量和降水量在 1965～1984年都表现出通过检验的显著性振荡且在 1977～1982年振荡最显著;对比图 2(a)(c)可知,在 2～4 a周期尺度上,两者在 1959～1969年以及 1983～1984年也都表现出通过检验显著性振荡。这说明当阳市降水量和气温与水稻产量之间存在着不同程度的时频域相关。

3.3 水稻产量与气候变化的相关

两个时间序列的互相关系数只能表示两者的总体相关程度,难以反映两者之间的相关随频率和时间变化的具体细节。交叉小波变换的优点在于将气候信号在时间域和频率域中展开,而且对于高频振荡采用逐渐精细的频率域和时间域步长,从而可以分析信号变化的任何细节[13]。

图 3给出了当阳市气候产量与降水量年以及气温的交叉小波变化。图 3(a)(b)中等值线数值为气候产量与降水量以及气温的交叉小波系数,其中＞0表示正相关 (实线),＜0表示负相关 (虚线)。图 3(c)反映了气候产量与降水量 (实线)以及气候产量与气温 (虚线)的交叉小波相关系数在频率域中的分布,其中＞0表示正相关,＜0表示负相关。

图 3 气候产量与降水量年距平 (a)、气温年距平(b)交叉小波变换以及交叉谱密度 (c)

图 3(a)反映了当阳市气候产量与降水量的相关变化。对应 2-4 a周期尺度的振荡,在 1963～1969年以及 1975～1984年,两列信号显出较强的负相关关系;对应 5 a周期尺度的振荡,在 1984年之后年两列信号显出弱的负相关关系;对应 6～8 a周期尺度的震荡,在 1969年之前以及 1978年之后两列信号显出弱的负相关关系;对应准 10 a周期尺度的振荡,几乎整个时域两列信号都显示较弱的负相关关系。正相关的周期特征变化主要为对应 16 a的整个时段、对应 6～8 a周期尺度振荡的 1969～1977年、对应 5 a周期尺度振荡的 1984年以前以及对应 2～4 a周期尺度振荡的 1963年以前、1970～1974年以及 1984年以后。

图 3(b)反映了当阳市气候产量与气温的相关变化。对应 16 a以上周期尺度的振荡,几乎整个时域两列信号都显示较弱的负相关关系;对应 10 a左右周期尺度的振荡,仅在 1982年以后两列信号显出弱的负相关关系;对应准 8 a周期尺度的振荡,在1973年以后两列信号均显出弱的负相关关系;对应准 5 a周期尺度的震荡,仅在 1971年以前两列信号显出较强的负相关关系;对应 2～4 a周期尺度的振荡,在 1963年以前、1969～1977年以及 1985年以后两列信号显出弱的负相关关系。而正相关的周期特征变化主要具体表现在对应 2～4 a、准 5 a以及10 a左右周期尺度振荡的其他时段。

图 3(c)给出了气候产量与降水量 (实线)以及气候产量与气温 (虚线)的交叉小波相关系数在频率域中的分布。由图可见,频率域中气候产量与降水量及气温之间的相关关系随振荡周期尺度的不同而不同,其中气候产量与降水量在 5 a和 9 a时间尺度上的相关程度最大,与气温在 11 a时间尺度的相关程度最大。在 2～4 a时间尺度上,产量与降水量呈弱负相关,与气温呈弱正相关;在准 5 a时间尺度上,产量与降水量呈强的正相关,而与气温呈弱的负相关;在准 6～10 a时间尺度上,产量与降水量呈强的负相关,与气温仅在 9 a尺度时呈现极弱的负相关,其它尺度呈弱正相关;在 11 a时间尺度上,产量与降水量呈较强负相关,与气温呈较强正相关;在 16～20 a时间尺度上,产量与降水量呈较强负相关,与气温呈弱的正相关;在 20 a以上尺度上,产量与降水量及气温相关性很弱。

4 小结

①近 40a来,当阳市气候产量与降水量都存在2-4 a以及准 5 a时间尺度的周期振荡,气候产量与气温都存在 10 a左右以及 20 a左右时间尺度的周期振荡。

②当阳市水稻气候产量与降水都具有 5 a以及2-4 a时间尺度的显著周期变化;气候产量与气温都具有 2-4 a时间尺度的显著周期变化,而且气候产量与降水量和气温在某些振荡强度上的时域分布具有某些相似性。

③对应不同周期尺度的振荡,水稻产量与降水量以及气温的相关性也发生着变化,总体来说水稻产量与降水量呈负相关,与气温呈正相关。具体表现为：气候产量与降水量在 2-4 a、6-10 a、11 a以及 16-20 a时间尺度上呈负相关而在准 5 a时间尺度上呈正相关,且在 5 a和 9 a时间尺度上的相关程度最大;气候产量与气温在 2-4 a、6-8 a、10-12 a以及 16-20 a时间尺度上呈正相关而在准 5 a以及9 a时间尺度上呈负相关,且在 11 a时间尺度的相关程度最大。

[1] 余本勋.黔西北高寒山区水稻产量与气象因子相关分析[J].安徽农业科学,2002,30(3)：370-372.

[2] 尹春梅,谢小立 .桃源县水稻产量的气候影响分析[J].中国农业气象,2008,29(4)：450-453.

[3] 陈俊钦 .作物产量与气候因子的关系分析 .福建省农业厅,53-56.

[4] 饰绍印,朴昌一 .延边地区水稻产量与气象条件关系的初步探讨[J].吉林农业科学,1964,1(2),75-82.

[5] 李永华,高阳华,张建平,唐云辉 .气候波动对重庆水稻产量的影响及对策[J].中国农业气象,2008,29(1)：75-78.

[6] 刘新安,崔玉香,王伯伦,杨晓军 .辽宁省水稻产量波动与气象条件的关系[J].沈阳农业大学学报,1993,24(3)：211-216.

[7] 何少斌,武晓梅,张全发 .山西省粮食产量的波动与降水量的分析[J].山西农业科学,1988,4：10-13.

[8] 李志斌,陈佑启,姚艳敏,石淑芹 .建国以来黑龙江省粮食产量变化小波分析 [J].干旱区资源与环境 .2008,22(2)：128-132.

[9] 徐宁娣 .弋阳县水稻产量与气象条件关系的分析 .弋阳县气象局 .12.5-12.6

[10] 李春云 .用加权平均回归法求解趋势产量的探讨[J].气象,17(12),40-42.

[11] 温晓慧,温桂清,薛敏 .用直线滑动均值法做作物趋势产量预报[J].农业气象,1994：19-20.

[12] 周世怀 .指数平滑法在趋势产量预测上的应用及广东省早稻产量预报模式[J].热带气象,1987,3(3)：239-244.