基于System Generator的CORDIC算法DDS的FPGA实现

夏少峰，黄世震

(福州大学物理与信息工程学院，福州 350002)

在现代数字信号处理中，特别是在通信、雷达和导航等系统中高精度的DDS有着广泛的应用。近年来随着电子技术的迅速发展，传统的查表、多项式展开或近似的方法渐渐不能适应现代电子系统在速度、精度、简单性和高效实现方面的综合要求，而用CORDIC算法实现的DDS系统则能很好的兼顾这些方面，由于该算法仅涉及移位与加减运算，便于软硬件实现。因而受到了人们的广泛关注。目前该算法已经应用到FFT、DCT、DWT、DDFS以及极化调制等诸多领域。

本文先介绍DDS的原理，然后再从CORDIC算法的基本原理出发，论述了其流水线结构的FPGA实现的具体方法及其system generator模型，文中的模型经ISE编译并经过modelsim验证通过，仿真结果表明文中的设计方法是完全可行的，且运算结果具有较高的精度。

1 DDS原理

DDS一般由相位累加器、相幅转换器组成。具体工作原理为：相位累加器在时钟控制下以频率控制字为步长进行累加，累加的结果经过量化处理后送入相幅转换器输出为正弦和余弦波形。 DDS的输出频率为F=FcwFclk/2N，频率分辨率Δf=Fclk/2N，其中Fcw为频率控制字， Fclk为系统时钟频率， N为频率控制字的字长。

传统的相幅转换器采用查找表结构，为了达到高分辨率和较高的频谱程度， Fcw一般取值较大，本文的频率控制字为32位，如果存储全部的正、余弦值，需要大量的ROM资源，这在实际应用是不现实的。而采用CORDIC算法代替查找表结构的相幅转换器既能满足高精度、高分辨率、实时运算的要求，又减少了ROM资源，是一种好的实现方法。

2 CORDIC算法原理

CORDIC算法主要用于三角函数、对数、指数函数的计算。它的工作模式分为圆周模式和矢量模式。 DDS产生的正、余弦信号主要采用圆周模式。具体原理如下：初始向量A(xi， yi)依据一定的角度序列顺时针或逆时针旋转， 逐渐逼近目标角度B(xi+1， yi+1)。假设旋转N次，每次的旋转角度为θi，则第i次的旋转公式表示为：

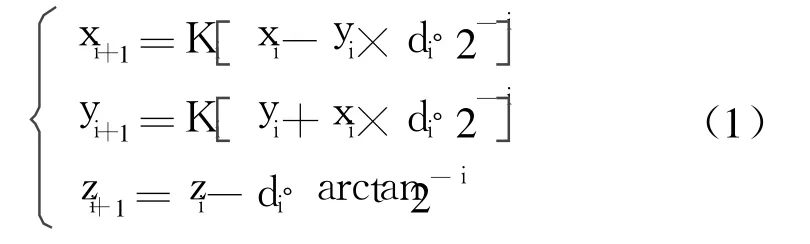
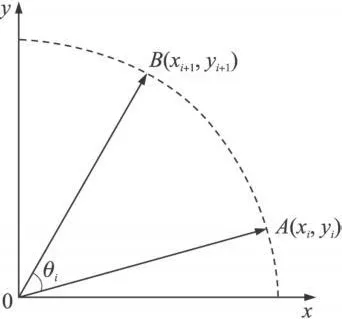
经过约定tanθ=2-i，即θi=arctan2-i，提出cosθi后di决定了旋转方向， di=+1表示按顺时针方向旋转， di=-1表示按逆时针方向旋转，其中di的数值由zi的符号位决定，在高速数字信号迭代结果后乘以模矫正因子：

3 DDS系统的设计

对于一个数字系统，系统的运算速度已经成为衡量系统性能的一个重要指标。而采用流水线设计是提高其运算速度的有效方法。流水线设计方法的基本思想是将一个完整的操作分成若干个时间上均衡的分段操作，从流水线的起点连续地输入，流水线的各操作段以重叠方式执行。这使得操作执行速度只与流水线输入的速度有关，而与处理所需的时间无关。这样，在理想的流水操作状态下其运行效率很高。

3.1 相位累加器设计

相位累加器由32位加法器和寄存器组成，其中又加入了抖动电路，如图1所示。因为相位截断给输出信号引入了周期性的杂散，因此设法破坏杂散的周期性及其与信号的相关性，可以有效地抑制相位截断带来的误差。抖动注入能打破相位截断误差的周期性，采用抖动注入后的杂散抑制可达到与增加2 bit相位寻址相同的效果。在每次累加器溢出时，产生一个随机整数加到累加器上，使相位累加器的溢出随机性的提前，从而打破周期性，抑制了杂散。

图1 相位累加器

3.2 相幅转换器设计和输出

相幅转换器设计采用图2所示的结构， 截位器truncate截取相位累加器累加后结果的高16位，作为相幅转换器的相位输入。

图2 相幅截位器

由于 CORDIC算法所能覆盖的角度范围为[ -99.8°， +99.8°]，为了能够达到[ -180°， +180°]角度的全覆盖，本module采用分象限法来解决角度覆盖问题。文中采用两个truncate模块来实现角度的转换，即在16位相位输入中用truncate1来截取高2位作为输出波形的相位控制信号。用truncate4截取低14位用来代表第一象限的[0°， 90°]。通过分析控制信号与三角函数之间的关系，来控制输出角度范围在[ -180°， +180°]内。另外由于CORDIC算法采用了流水线结构，导致了16(图中18表示还有实现因子k所引入的两个时钟延时)个时钟周期的延时，为了保证控制信号能够与CORDIC运算器输出同步，在控制器后插入了一个18个时钟周期的延时单元。通过延时后的两个控制信号控制输出完整的正、余弦波形。具体的控制逻辑电路如图3所示。

图3 输出转换器

3.3 CORDIC运算器设计

CORDIC运算器设计采用图4所示结构， 图4上部是16阶中的第2阶，由于CORDIC算法中每一次的迭代公式都一样，所以其他16阶结构是完全相同，且只有移位和加/减运算，易于采用流水线技术来提高其运算速度。其中加减法器上所加的寄存器即是用来实现流水线操作的。图4下部为迭代次数N=16时的全流水线结构。

设定初始向量X0=1◦215、Y0=0、Z0=θ，经过N次迭代后， Xn=cosθ、Yn=sinθ、Zn=0。 (cordic_gain实现乘模矫正因子功能)CORDIC运算器输入角度范围为[0°， 90°]， 输出为该角度范围内的正、余弦波形。

图4 CORDIC运算器设计

4 仿真验证

本仿真环境是matlab7.5.0 的simulink通信仿真工具箱。用matlab集成工具sptool查得输出正旋波的频域结果如图5所示，从图5 中可以看到此方法完全实现了所需的正旋波，并且cordic产生的正弦信号的无杂散动态范围SFDR(无杂散动态范围)约为-83 db。

图5 频域仿真结果

另外用matlab集成工具system generator直接生成verilog代码并在modelsim中进行仿真，得到的局部仿真结果如图6所示。从结果可以看出，成功的用system generator工具实现了cordic算法的dds发生器。

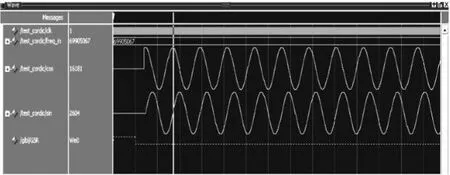
图6 modelsim仿真结果

5 结语

文中介绍了一种新型的算法级的FPGA设计方法，并成功的利用system generator完成了cordic算法的DDS设计，给出了详细的设计过程，而且对数字部分进行了仿真。这种方法的优点在于它可以从系统框图(模型)直接转化成HDL语言，省去了代码的繁杂编写任务，实现了系统的快速设计。

本文作者创新点，加入了两个关键技术：抖动注入和1/4象限旋转覆盖，此方法既提高了输出信号的SFDR，又节省了硬件资源。

[ 1] 门爱东，杨波，全子一.数字信号处理[ M] .北京：人民邮电出版社， 2003.

[ 2] 胡广书.现代信号处理教程[ M] .北京：清华大学出版社， 2004.

[ 3] 张雅绮，李锵译.(美)Michael D Ciletti著.Verilog HDL高级数字设计[ M] .北京：电子工业出版社， 2005.

[ 4] 田耕，徐文波，张延伟.无线通信FPGA设计[ M] .北京：电子工业出版社， 2008.

[ 5] Volder J.The CORDIC Computing Technique[ J] .IRE Trans.Comput.， Sept.1959.

[ 6] Despain A M.Fourier Tansform Computers Using CORDIC Iterations[ J] .IEEE Trans.Comput.， May 1984.

[ 7] Ercegovac M D， Lang T.Implementation of Fast Angle Calculation and Rotation Using Online Cordic[ C] //Proc.ISCAS' 88， 2703-2706.