基于多智能体粒子群算法的盲均衡技术研究

张福洪，朱芳英

(杭州电子科技大学通信工程学院， 杭州310018)

数字通信系统中，为了克服码间干扰，正确恢复发送序列，须在接收端采用均衡器。盲均衡技术不需要借助训练序列，仅利用接收序列本身的先验知识来均衡信道，使其输出序列尽可能的逼近发送序列[1]。目前，盲均衡技术可以分为三类：BUSSGANG类算法、基于高阶或循环统计量算法和非线性均衡算法。第一类算法中的常模算法(CMA)[2]通过对接收信号取模运算将二维QAM信号映射到一维空间，然后在一维空间确定代价函数，这类算法实现简单，得到了广泛的应用，但是运算中损失了信号的相位信息。由于高阶累积量HOC(Higher OrderCumulants)[3]对高斯噪声有很强的抑制效果，引起了许多学者的关注。上述前两种均衡算法都采用梯度搜索方法获得最优解，但梯度算法易陷入局部收敛，难以获得全局最优。最近，有人把遗传算法应用于盲均衡问题[4]中，但遗传算法易陷入局部最优，不能获得全局最优的性能。本文提出基于粒子群算法的盲均衡技术，在较少的迭代次数下即可获得全局最优的性能，仿真结果表明，本文算法有较好的性能。

1 盲均衡代价函数

盲均衡原理框图如图1所示。

图1 盲均衡原理框图

对于一个稳定的、可逆的线性卷积系统，盲均衡的输入序列为：

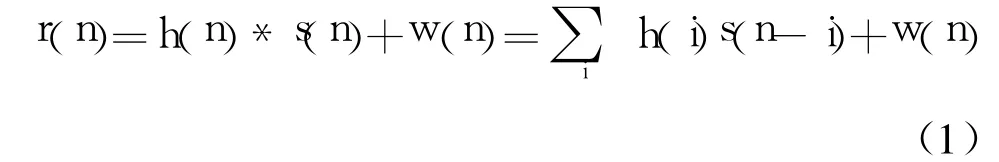
式中r(n)为观测信号， h(n)为非最小相位的线性时不变系统， w(n)为加性高斯白噪声， “*”表示信号的卷积。

在不考虑加性高斯白噪声的情况下，均衡器的输出信号为：

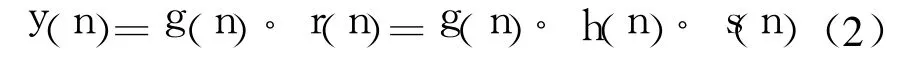
盲均衡的目的就是使

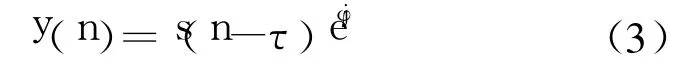
式中τ为一整数时延， φ为一常数相移。为了满足式(3)， h(n)与g(n)组成的联合冲击响应为：b(n)中只有唯一的非零元素βeθ，其中β 和θ分别表示理想系统的幅度和相位因子。

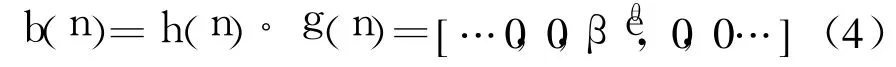
1.1 多模算法(MMA)代价函数

Godard算法广泛地应用于实际的盲均衡器中，适用于具有恒定包络的发射信号的均衡。常模算法是其中最常用的算法。但由于常模算法是盲相位算法，对相位不敏感，当系统的载波频率或信道存在相位旋转时，均衡器收敛后的输出信号有一个任意的相位旋转。为了克服此缺陷，已提出的多模算法代价函数中包含了多个(至少两个)常数模值。 MMA是通过把CMA代价函数中均衡器输出信号的实部和虚部离开得到的，其代价函数为

1.2 基于高阶累积量的代价函数

对于16 QAM信号，其均衡后的信号y(n)的二阶和四阶累积量定义为：

其中， y表示均衡器输出信号的向量， y*表示y的共轭。

文献[5]给出了一种代价函数：

其中二阶累积量C2，y不为零。由文献[6]可知：

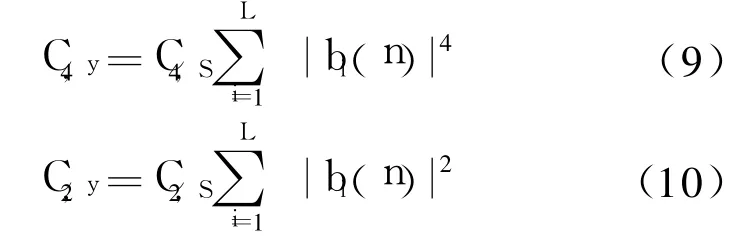
式中C2，S和C4，S分别为发送序列s(n)的二阶和四阶累积量。L为均衡器抽头的个数， b(n)为定义的联合冲击响应；则代价函数可以重新写为：

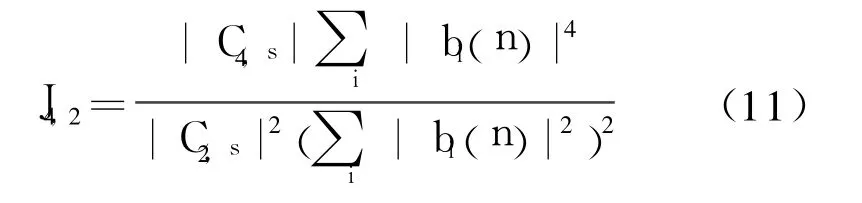
由于

易知

当且仅当b(n)中有唯一的非零元素时取等号才成立。由式(7)～式(11)可推知：

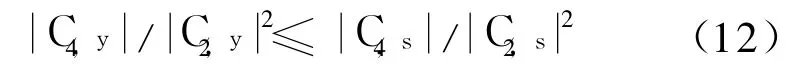
这样最大化J4，2就可以实现盲均衡。

2 基于粒子群算法的盲均衡

2.1 粒子群算法

设粒子群[7]中粒子个数为S，则在一个D维的搜索空间中，粒子i(1≤i≤S)在第k次迭代时的位置信息可以表示为，速度信息表示为，粒子到目前为止所经历的最好位置为，群体中所有粒子到目前为止所经历过的最好位置为，其中b为具有最优位置粒子的索引。在这里，所谓的“最好位置”即为适应度最高的解。粒子群算法的进化方程可描述为[6]：

其中， d表示粒子的第d维(1≤d≤D)， ω为惯性权重， c1和c2为学习因子(也称加速常数)， r1和r2为分布于[0， 1]间的随机数。为了减少在进化过程中粒子离开搜索空间的可能性，粒子速度通常限定在一定范围内，即

2.2 基于粒子群算法的盲均衡方法

将粒子群算法应用于盲均衡，需要构造合适的适应度函数。对于式(5)，取fMMA=1/JMMA作为适应度函数，基于高阶累积量的代价函数取f4，2=J4，2作为适应度函数。

基于粒子群算法分别以fMMA和f4，2作为适应度函数的盲均衡方法分别称为：粒子群多模盲均衡(PSOMMA)和基于粒子群的高阶累积量盲均衡(PSOHOC)，得到基于粒子群算法的盲均衡方法的基本步骤如下：

步骤1 初始化种群，随机产生S个粒子的种群，并随机产生每个粒子的位置和速度；

步骤2 分别以fD、 fMMA和f4，2作为适应度函数并计算适应度， 保存全局最优解 pkgd和局部最优解pkid

步骤3 根据式(13)和式(14)更新粒子的速度和位置；

步骤4 重新计算适应度值，更新pkgd和pkid；

步骤5 如果达到最大迭代次数，算法终止；否则，转至步骤3。

3 性能仿真与分析

信道参数设置为：信道冲击响应h(n)如表1所示，信号源为16 QAM信号，均衡器采用11个抽头系数，初始值随机产生，输入端信噪比为30 dB，接收信号星座图如图2所示。 PSO的参数设置为：种群数为30，循环迭代次数为800。算法性能采用收敛后的均衡器输出星座图和码间干扰(ISI)来表示。

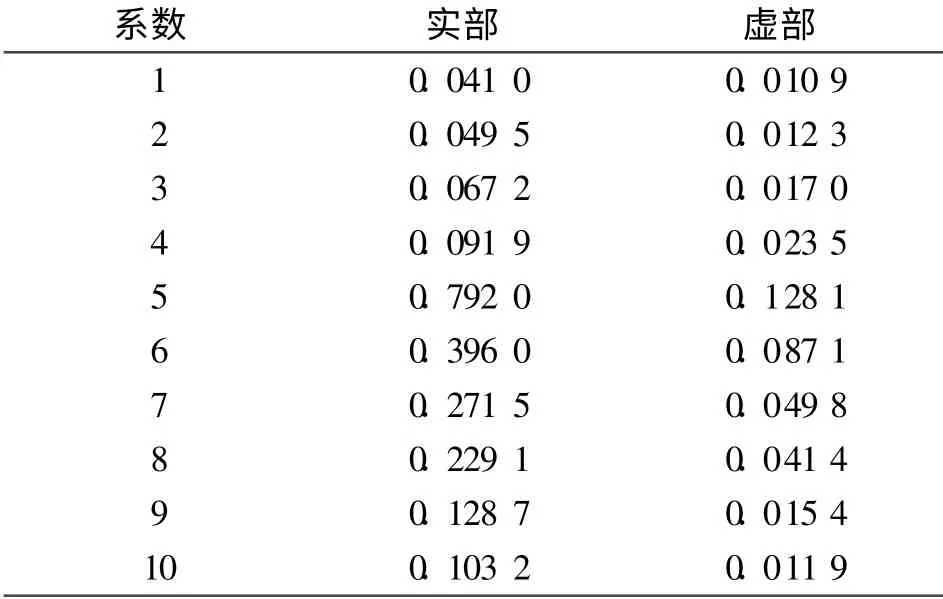
表1 信道的冲击响应

码间干扰定义为

图2给出了在信噪比为30 dB情况下均衡器输入信号的星座图。

图3给出了码间干扰和迭代次数的关系。为了比较算法性能，采用的均衡器有：基于遗传算法的常模盲均衡(GACMA)[8]，基于遗传算法的多模盲均衡(GAMMA)、PSOMMA和PSOHOC。由图可见，信道的初始码间干扰为-1.2386 dB， PSOHOC有较快的收敛速度，在200次迭代以后开始收敛，且均衡输出码间干扰为-25.656 dB，降低了24.4174 dB；PSOMMA在300次迭代以后收敛，均衡输出码间干扰为-22.674 dB，降低了21.4354 dB；GAMMA在650 次迭代以后收敛，均衡输出的码间干扰为-19.717 dB，降低了18.4784 dB；而GACMA在750次迭代以后收敛，均衡输出的码间干扰为-16.247，降低了15.0084 dB，所以基于粒子群算法的高阶累积量盲均衡算法有较快的收敛速度，且收敛后的干扰较小。

图2 接收信号星座图

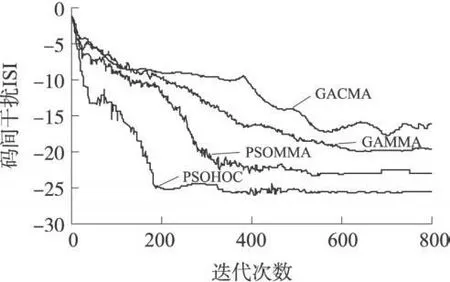
图3 码间干扰与迭代次数的关系曲线

图4给出了PSOMMA算法的输出信号星座图。PSOMMA的信号均衡效果较好，没有相位偏移。

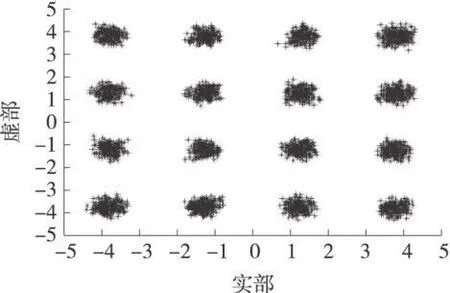
图4 多模准则的均衡器输出信号星座图

图5出了PSOHOC算法的输出信号星座图。由图可知， PSOHOC算法不但均衡效果好，而且没有相位偏移。

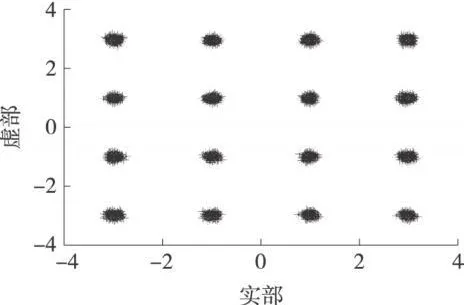
图5 高阶累积量准则的均衡器输出信号星座图

4 结束语

由于梯度搜索存在局部最优收敛的缺点，本文把常模准则、多模准则、高阶累积量准则分别结合粒子群算法，提出新的解决盲均衡问题的方法。通过计算机仿真表明，本文所提出的新的算法，不但有较快的收敛速度，且收敛后性能较优，证明了本算法的实用性。

[ 1] 赵知劲，陈刚.盲均衡的发展[ J].杭州电子工业学院学报，2000， 20(6)：61-64.

[ 2] Godard D.Self-Recovering Equalization and Carrier Tracking in Two-dimensional Data Communication Systems[ J] .IEEE Trans.on Commn.， 1980， 28(11)：1867-1875.

[ 3] 何晓薇，樊龙飞.基于二阶、四阶累计量的盲解卷机准则[ J] .电子科技大学学报， 1998(4)：27-30.

[ 4] 郑鹏，尤春艳，刘郁林，等.基于最大峰度准则和遗传算法的盲辨识与盲均衡[ J] .重庆邮电学院学报， 2004， 16(4)：64-67.

[ 5] 陈金召，郑鹏，尤春艳.用遗传算法求解基于高阶累积量的盲均衡问题[ J] .现代电子技术， 2003， 24：64-66.

[ 6] 张贤达，保铮.通信信号处理[ M].北京：国防工业出版社， 2000.

[ 7] Kennedy J， Eberhart R.Particle Swarm Optimization[C] //IEEE International Conference on Neural Networks， 1995， 4：1942-1948.

[ 8]Liu Feng， Ge Lin-dong， Wu Ye-jin， et al.Blind Equalization Based on Immune Optimized Genetic Algorithm[ C] //2008 9th International Conference on Signal processing Proceedings， 2008， 2：1719-1721.