SiGe HBT直流电流增益模型研究

王 颖

(陕西教育学院基建处， 西安710061)

直流电流增益是表征双极晶体管直流性能的重要参数。对于SiGe HBT(异质结双极晶体管)，发射结为Si/SiGe异质结，其禁带宽度差可以有效地提高发射结的载流子注入效率，使得SiGe HBT直流电流增益可以做的很高。

虽然， SiGe HBT的直流电流增益在理论上可以做得很大，但实际上并非如此，据报道这主要是由于器件物理、结构参数和各种复合电流引起的[1-5]。因此，建立SiGe HBT直流电流增益模型，定量的分析器件物理、结构参数以及复合电流与增益的关系，对SiGe HBT的设计与制造具有重要的指导意义[6-9]。

1 直流电流增益模型

直流电流增益的大小直接表示了双极晶体管的直流放大能力，即

式中， IC为集电极电流， IB为基极电流

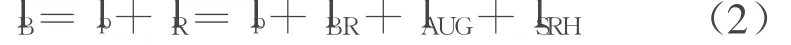
式中， Ip为空穴反注入电流， IR为复合电流，主要包含中性基区复合电流IBR，空间电荷区俄歇复合电流IAUG，空间电荷区SRH复合ISRH。

1.1 集电极电流密度模型

1.1.1 小电流下集电极电流密度模型

相对集电极电流密度JC， SiGe HBT基极电流很小，因而近似认为基区中电流恒定。电流密度采用漂移扩散方程为[10]

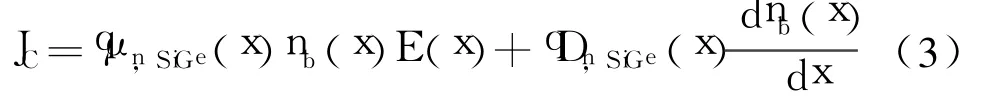
式中， μn，SiGe(x)为SiGe基区电子迁移率[9]， Dn，SiGe(x)为SiGe基区电子扩散系数， E(x)为基区自建电场[10]，

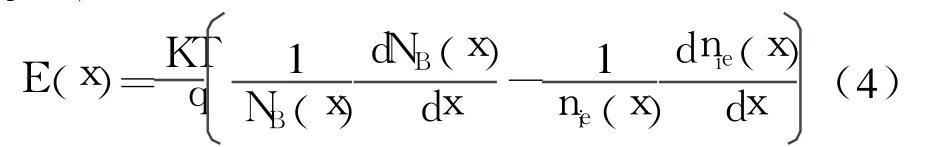
而nb(x)为基区少子密度[10]

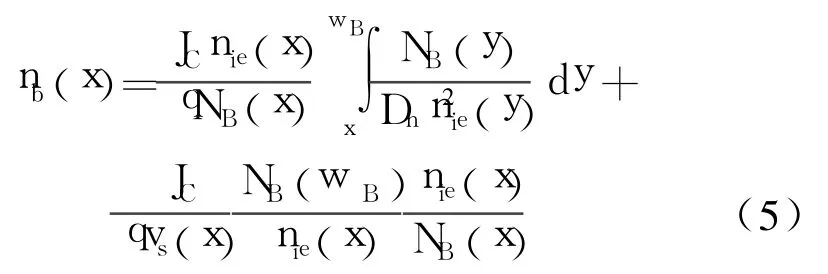
式中， vs(x)为电子的传输速度， Dn为基区少子的扩散系数， wB为基区宽度。

由式(3)、式(4)可以得到，

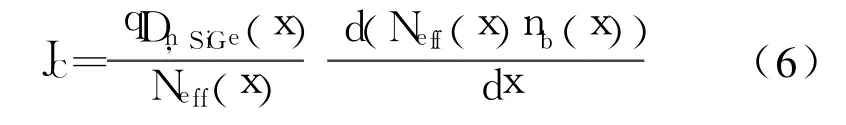
对式(6)从0→wB积分可得，

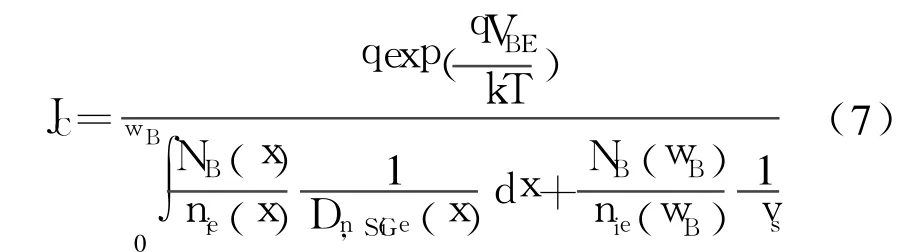
式中， VBE是BE结正偏电压， vs是电子饱和速度。

1.1.2 大电流下集电极电流密度模型

在大电流下，基区中任意一点少子浓度nb(x)值都可以和该点的杂质浓度NB(x)值比拟。因此，此时计算集电极电流密度，就应当充分考虑少子浓度的影响。本文中近似认为在10nb(0)＞NB(0)时，就应当考虑少子浓度的影响。

在大电流下，基区自建电场强度为[6]

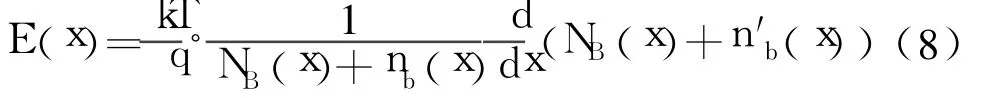
此时，式中基区中少子浓度

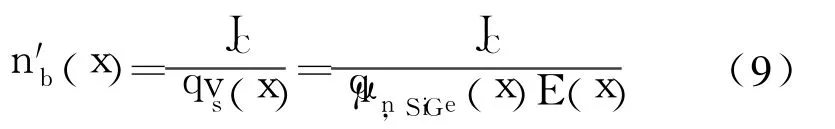
其中， vs(x)为基区中少子传输速度，将式(8)代入式(7)得

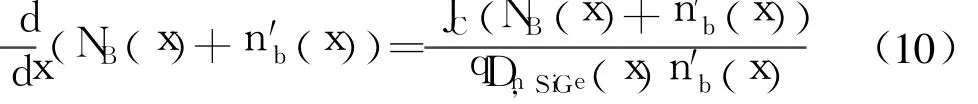
而基区中电子电流密度[10]为

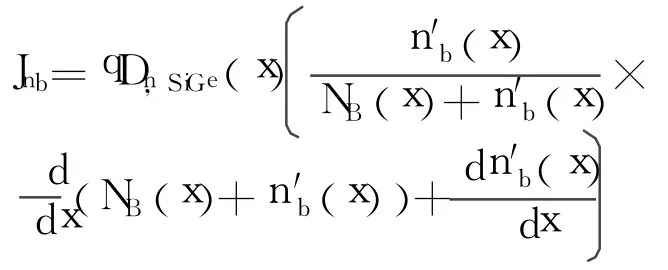
即，

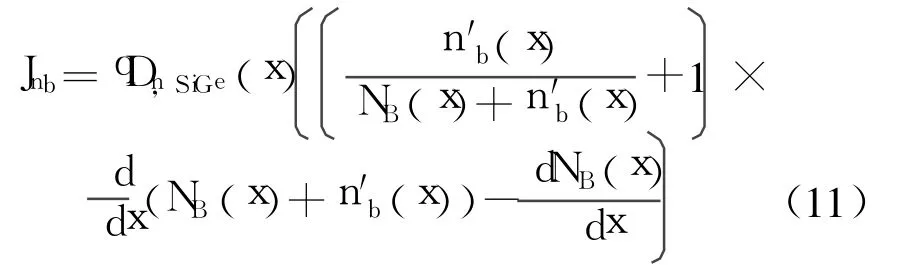
基区电子电流为常数，则JC=Jnb。将(10)式代入(11)式，得

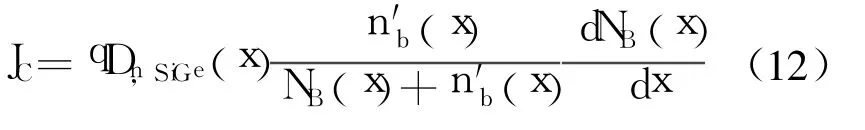
以集电结界面为坐标原点，由式(11)得

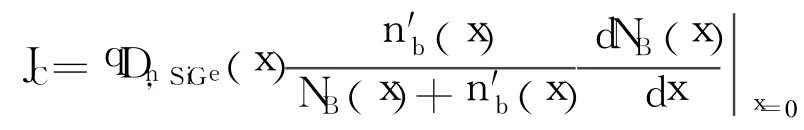
即，

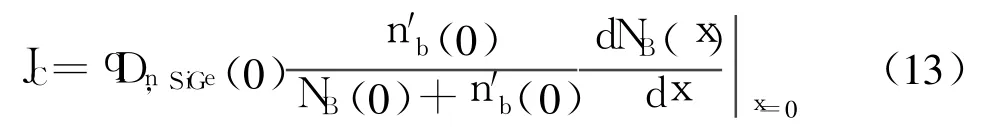
式中，

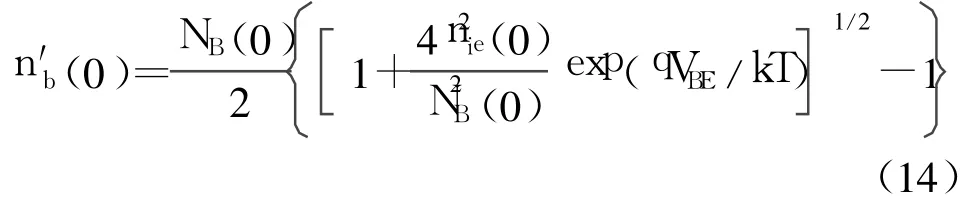
1.2 空穴反注入电流密度

在发射区中设杂质NE为均匀分布，其空穴电流的漂移扩散方程为

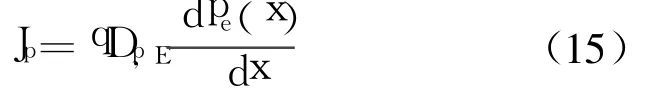
式中， Dp，Si为发射区中空穴扩散系数， pe(x)为发射区中少子载流子浓度分布，对式(15)在空穴扩散长度内积分，则

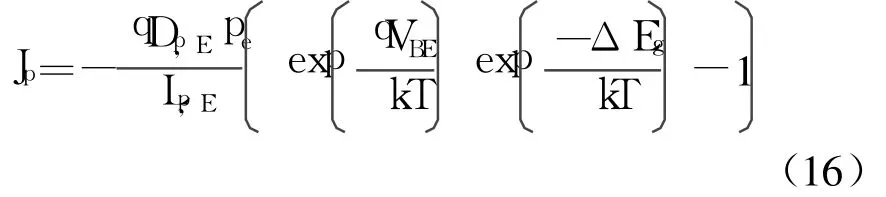
式中， ΔEg为发射结两侧禁带差， Lp，E为发射区中空穴的扩散长度， VBE为发射结偏压， pe0为扩散长度以外区域的空穴浓度，即ni为Si的本征载流子浓度。

1.3 复合电流

1.3.1 中性基区复合电流

由于基区中有足够多的空穴，因而基区中复合是由电子浓度决定的。基区中的少子分布近似呈指数分布，所以基区中的少子寿命用指数形式近似[11]

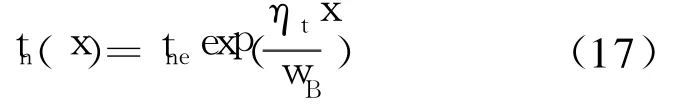
式中，

其中， tne和tnc分别为基区中发射结侧和集电结侧的少子寿命。少子寿命也会因工艺的优劣可以在0.1 ～100 ns范围内变化，有的甚至小到10-13s[12]。

(1)小电流下的中性基区复合电流

在dx内的中性基区复合电流为

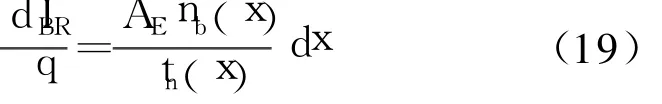
对(19)式从0→wB积分可得：

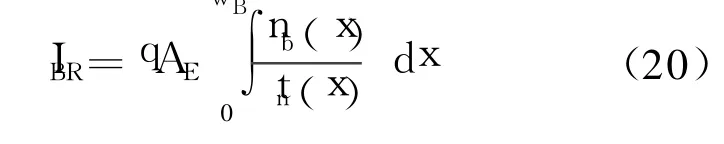
即

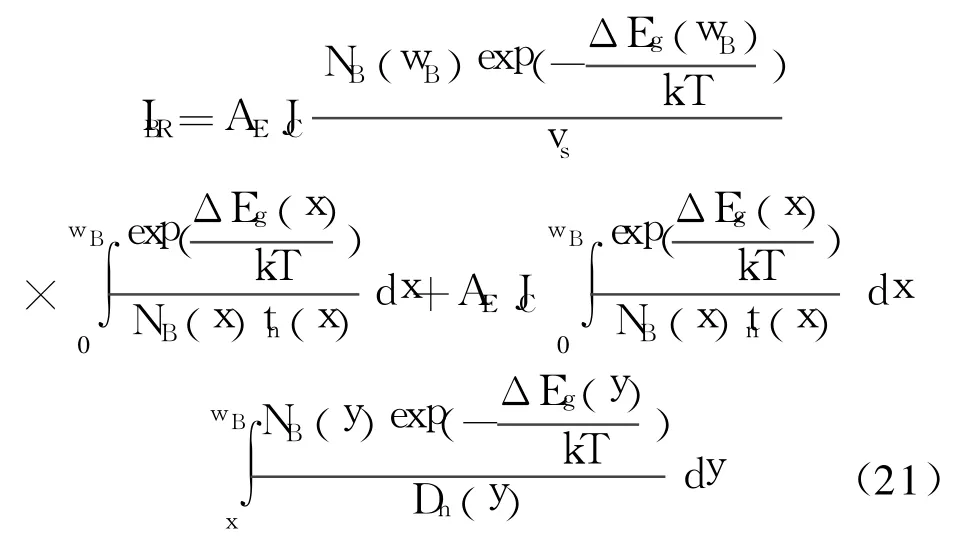
AE为发射结面积， ΔEg(x)为基区中任意位置与发射区的禁带差[10]。

(2)基区扩展情况下的中性基区复合电流

随着电流增大，基区要发生扩展，因而基区宽度要变宽，中性基区复合电流要增大。这也是大电流下增益下降的原因之一。此时中性基区复合电流可以分成两部分：1)本征基区的复合电流， 2)电流感应基区的复合电流。前一部分已求出，此处仅须求出后一部分。在电流感应基区中，掺杂较低，且一般为均匀分布，同时为了处理的方便，认为此区中的少子寿命为常数。

设在感应基区边界处， 少子的浓度为ns，在这个区以线性分布近似可以得到这部分复合电流为：

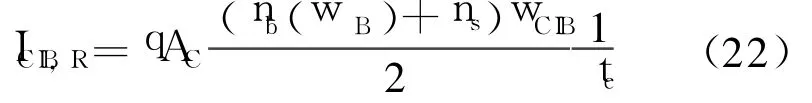
式中， AC为集电结面积， wCIB为基区扩展宽度， tc为感应基区的少子寿命，这个区为Si材料，因而可以采用Si中的少子寿命模型，边界处少子的浓度

因而此时总的基区复合电流为

1.3.2 空间电荷区中的复合电流

空间电荷区的复合电流是小电流下增益下降的主要原因。该电流分为两部分：通过复合中心的SRH(Shockley-Read-Hall)复合电流和带间俄歇复合电流。

(1)SRH复合

由复合理论，在稳态下情况下，载流子的净复合率为[13]

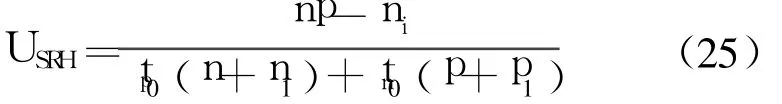
式中，

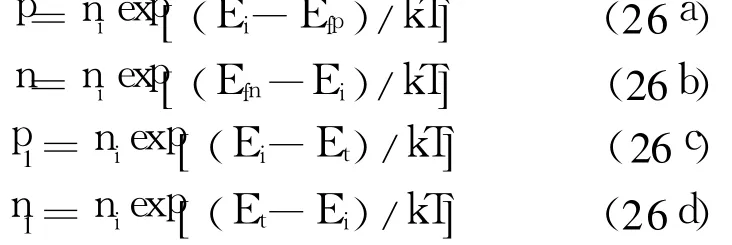
式中， Ei为本征能级， Et为复合中心能级， tn0、tp0分别为空间电荷区内电子，空穴的寿命， Efn、Efp分别为电子和空穴的准费米能级，则

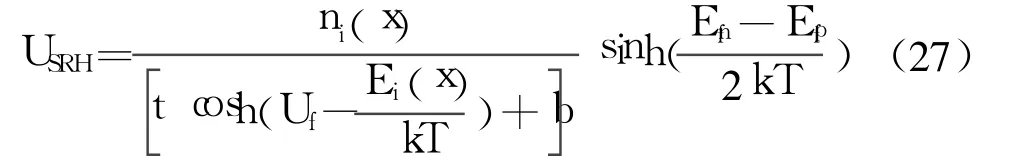
式中，

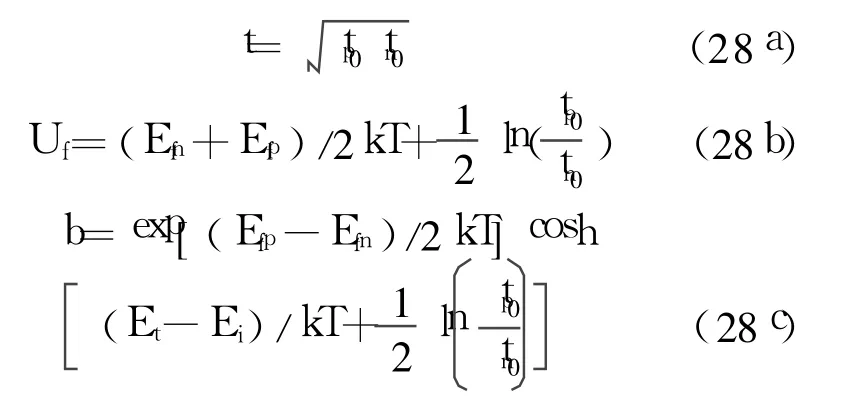
当复合中心能级满足：Et=Ei时， b可以忽略。在SiGe HBT的发射结中，可认为ΔEi=0， Efn、Efp在空间电荷区内没有弯曲， ni在发射结中虽然不是常数，但若按突变结处理，则在Si区和SiGe区中分别为常数。因而(27)式中只有一个Ei(x)为位置的函数。若选x=xpe处的本征能级的电势为零，则可以得到

式中φ(x)为静电势。应用耗尽层近似可得到

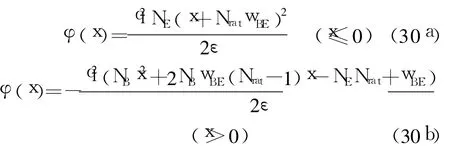
式中，

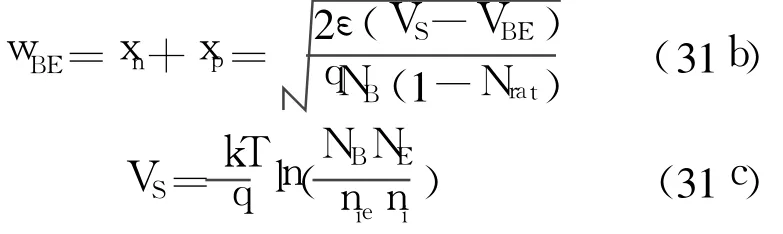
空间电荷区中由于SRH复合引起的电流为

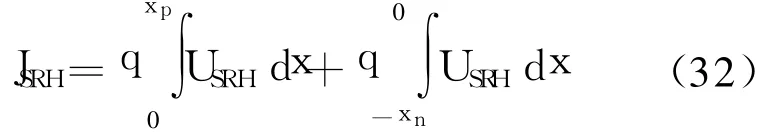
由于(30)式形式较为复杂，积分难以获得解析解，为了获得解析解可以用线性函数对(30)式近似替代

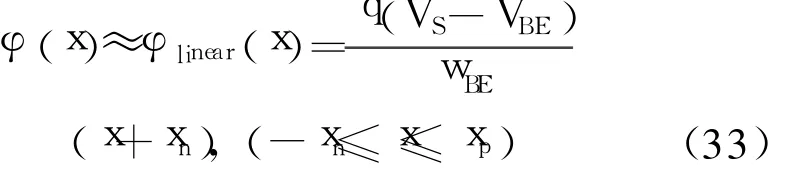
式中，

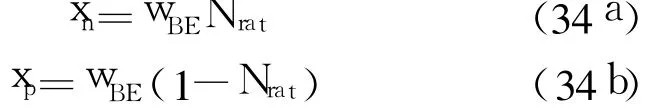
(2)俄歇复合

当掺杂浓度增加时，俄歇复合变得越来越重要了。俄歇复合是一个三粒子过程，其有两个过程：1)一个导带电子复合一个空穴，将能量传递给一个空穴；2)一个价带空穴复合一个导带电子，将能量传递给一个电子。第一种情况复合率正比于p2n，第二种情况则正比于pn2。因此俄歇复合率可以表示为[13]

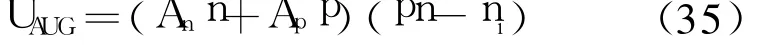
式中， p和n分别为空间电荷区中空穴和电子的浓度， An/Ap分别为电子和空穴的复合系数。上式也可以表示为

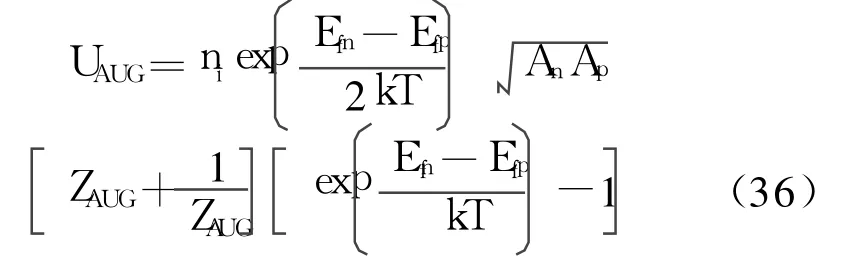
式中，

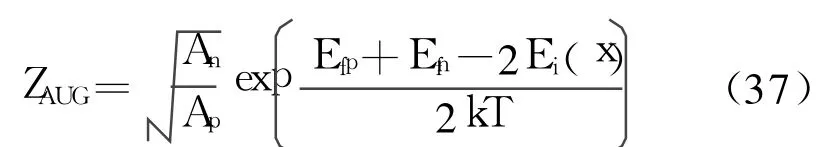
根据(36)式可以得到俄歇复合电流为

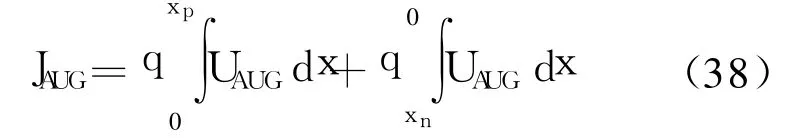
和SRH复合处理方法一样，利用φ(x)近似的方法，可以得到俄歇复合电流的解析表达式。

2 模拟结果与讨论

发射区掺杂为 4 ×1017cm-3， 发射结面积为30 μm2，集电结面积为50 μm2，基区宽度为50 nm，掺杂为 1×1019cm-3， Ge组分分别为 0.13、0.14、0.15时， SiGe HBT直流电流增益随集电极电流的变化关系，如图1所示。

从图1可以看出，基区中的Ge组分含量对电流增益有强烈的影响，随着基区Ge组分的增加，电流增益显著增大，这是因为随着基区Ge组分的增加，异质发射结的禁带差增加，空穴从基区进入发射区的势垒高度也随之增加，因此空穴反向注入电流减小，电流增益增大。

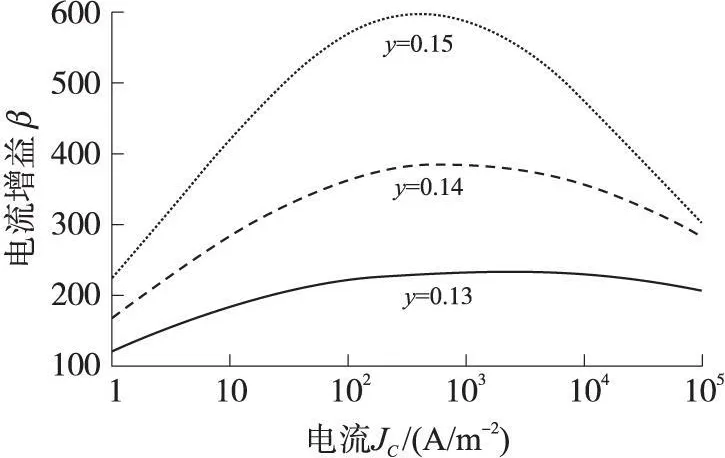
图1 不同的Ge组分下电流增益与集电极电流密度的关系

在曲线开始部分，随电流的增加，其增益增加，这是因为在小电流下，组成基极电流的三种电流中，发射极空间电荷区的复合电流占的比重最大，所以此时电流增益要小，随电流的增大，此项复合电流的增加速率较慢，所以在较大的电流下比重下降，增益增加。当出现基区扩展效应后，其电流增益要迅速减小，因为电流感应基区也存在复合电流，基极电流增加。

其它条件不变，基区Ge组分为0.15，基区掺杂浓度分别为1 ×1019cm-3、3×1019cm-3、5 ×1019cm-3时， SiGe HBT直流电流增益随集电极电流的变化关系，如图2所示。

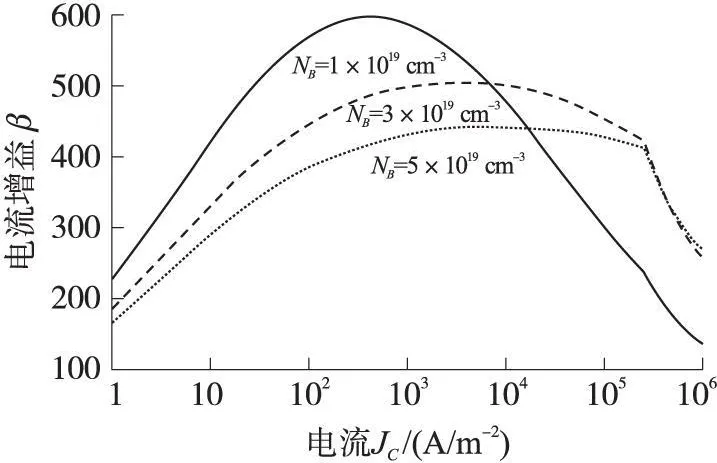
图2 不同的基区掺杂浓度下电流增益与集电极电流密度的关系

从图2中可以看到，随着基区掺杂浓度的增加，电流增益下降，这是因为随着基区掺杂浓度的增加空间电荷区也随之增大，空间电荷区的复合电流也随之增大，因此，电流增益下降。

其它条件不变，基区Ge组分为0.15，基区掺杂浓度为 1 ×1019cm-3， 基区宽度分别为 40 nm、50 nm、60 nm时， SiGe HBT直流电流增益随集电极电流的变化关系，如图3所示。

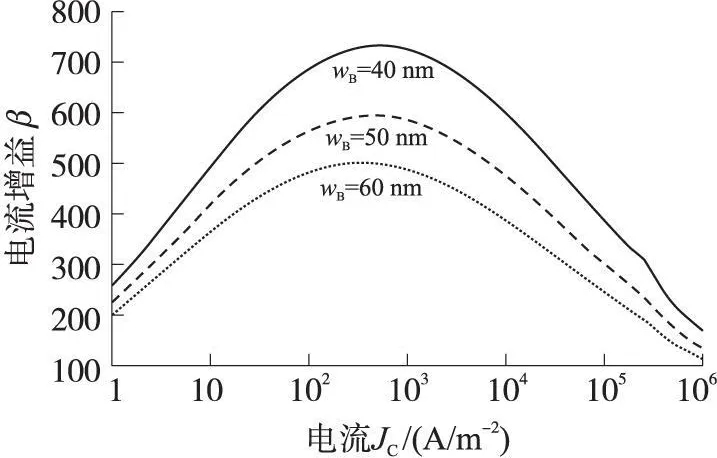
图3 不同的基区宽度下电流增益与集电极电流密度的关系

从图3中可以看到，随着基区宽度的增加，电流增益下降，这是因为随着基区宽度的增加，中性基区复合电流也随之增大，因此，电流增益下降。

3 结论

本文基于SiGe HBT器件结构、电学特点，分别建立了SiGeHBT集电极电流密度，空穴反注入电流密度、中性基区复合电流、SRH电流密度和带间俄歇复合电流密度模型，并在此基础上建立了直流电流增益模型，并进行了模拟仿真，分析了器件物理、结构参数以及复合电流与增益的关系，得到了SiGe HBT直流电流增益特性优化的理论依据。

[ 1] 宋建军，张鹤鸣， 戴显英， 等.第一性原理研究应变Si/(111)Si1-xGex能带结构[ J] .物理学报， 2008， 57(9)：5918-5922.

[ 2] 胡 辉 勇， 张 鹤 鸣， 吕 懿， 等.SiGe HBT大 信 号 等 效 电 路 模型[ J].物理学报， 2006， 55(1)：403-108.

[ 3] 吕懿，张鹤鸣，戴显英，等.SiGe HBT势垒电容模型[ J].物理学报， 2004， 53(9)：3239-3244.

[ 4] Patton Gary L， Iyer Subramanian S， DelageSylvain L， et al.Silicon-Germanium-Base Hetero-junction Bipolar Transistors By Molecular Beam Epitaxy[J] .IEEE Trans on Electron Devices Letter，1988， 9(4)：165-168.

[ 5] King Clifford A， Hoyt Judy L， Gibbons James F.Bandgap and Transport Properties of Si1-xGexbt Analysis of Nearly Ideal Si/Si1-xGex/Si Heterojunction Bipolar Transistors[ J] .IEEE Trans on Electron Devices， 1989， 36(10)：2093-2104.

[ 6] 林 大 松， 张 鹤 鸣， 戴 显 英， 等.SiGe HBT基 区 渡 越 时 间 模型[ J] .西安电子科技大学学报， 2001， 28(4)：456-461.

[ 7] 胡 辉 勇， 张 鹤 鸣， 戴 显 英， 等.SiGe HBT传 输 电 流 模 型 研究[ J] .半导体学报， 2006， 27(6)：1059-1063.

[ 8] Hu Huiyong， Zhang Hem ing， DaiX ianying， etal.Modelof Transit Time for SiGe HBT Collector Junction Depletion-Layer[ J].Chinese Physics， 2005， 14(7)：1439-1433.

[ 9] Makoto M， Hiromi S， Katsuya O， et al.Ultra-Low-Power SiGe HBT Technology for Wide-Range Microwave Applications[ C] //IEEE Bipolar/BiCMOS Circuits and Technology Meeting， 2008，129-132.

[ 10] 张鹤鸣，戴显英，林大松，等.SiGe HBT基区渡越时间与基区Ge组分剖面优化[J] .西安电子科技大学学报， 2000， 27(3)：305-308.

[ 11] Shafi Z A， Gibbings C J， Ashbum P， et al.The Importance of Neutral Base Recombination in Comprom ising the Gain of Si/SiGe Heterojunction Bipolar Transistors[ J] .IEEE Trans on Electron Devices， 1991， 38(8)：1973-1976.

[ 12] Ghani T， Hoyt J L， NobleD B， et al.Effect of Oxygen on Minority-Carrier Lifetime and Recombination Currents in Si1-xGexHeterostructure Devices[ J].Applied Physics Letter， 1991， 58(12)：1317-1319.

[ 13] Searles S， Pulfrey D L.An Analysis of Space-Charge-Region Recombination in HBT' s[ J] .IEEE Trans on Electron Devices，1994， 41(4)：476-483.王 颖(1978-)，女，助理工程师， 陕西教育学院基建处，主要研究方向为高速半导体器件及集成电路， 现代教育技术理论及应用， wy_9339@163.com。