基于ADS的平行耦合微带线带通滤波器的设计及优化
2010-12-21张福洪张振强马佳佳
张福洪,张振强,马佳佳
(杭州电子科技大学通信工程学院,杭州 310018)
滤波器是用来分离不同频率信号的一种器件。它的主要作用是抑制不需要的信号, 使其不能通过滤波器, 只让需要的信号通过。在微波电路系统中,滤波器的性能对电路的性能指标有很大的影响,因此如何设计出一个具有高性能的滤波器,对设计微波电路系统具有很重要的意义。微带电路具有体积小,重量轻、频带宽等诸多优点,近年来在微波电路系统应用广泛,其中用微带做滤波器是其主要应用之一。平行耦合微带线带通滤波器在微波集成电路中是被广为应用的带通滤波器。
1 基本原理[ 1]
当两个无屏蔽的传输线紧靠一起时,由于传输线之间电磁场的相互作用,在传输线之间会有功率耦合,这种传输线称之为耦合传输线。根据传输线理论,每条单独的微带线都等价为小段串联电感和小段并联电容。每条微带线的特性阻抗为Z0,相互耦合的部分长度为L,微带线的宽度为W,微带线之间的距离为S,偶模特性阻抗为Ze,奇模特性阻抗为Z0。单个微带线单元虽然具有滤波特性,但其不能提供陡峭的通带到阻带的过渡。如果将多个单元级联,级联后的网络可以具有良好的滤波特性。
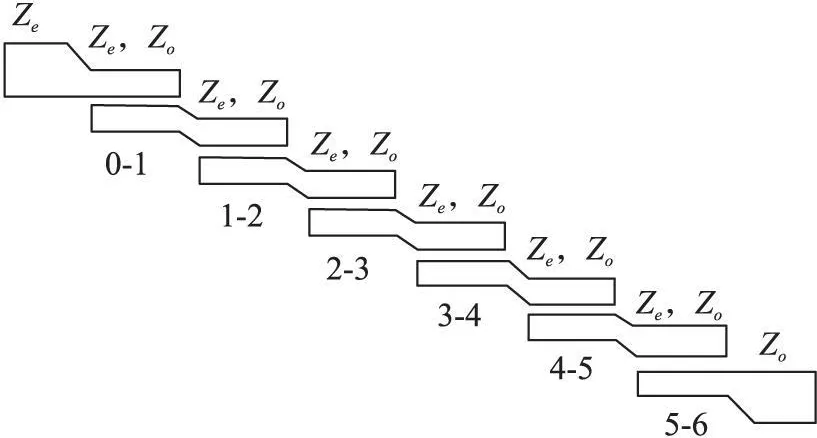
图1 5级耦合微带线带通滤波器[2]
2 设计步骤
2.1 设计低通原型
根据带通滤波器的一系列参数通过频率变换和查表选择低通原型滤波器的归一化原型参量[3]。用ω1和ω2表示带通滤波器的下边界和上边界, ω0表示中心频率。将带通滤波器变换为低通原型[5]。
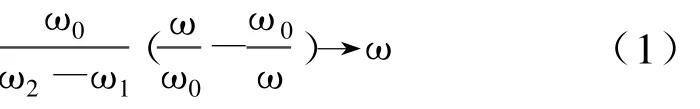
归一化带宽

查表得到归一化设计参数g1, g2...gNgN+1。
2.2 计算各节偶模和奇模的特性阻抗设计
用g1, g2...gNgN+1和BW确定带通滤波器电路中的设计参数耦合传输线的奇模和偶模的特性阻抗:
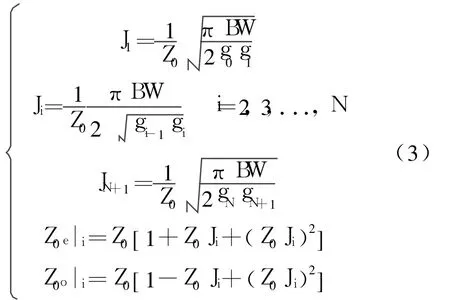
2.3 计算微带线的几何尺寸
根据微带线的偶模和奇模阻抗,按照给定的微带线路板的参数,使用ADS中的微带线计算器LineCalc计算得到微带线的几何尺寸W, S, L。
2.4 仿真及优化[ 4]
连接好电路,将计算出的W, S, L输入,扫描参数为S11, S21,进行仿真。一般来说用理论值的得到仿真结果和实际想要得到结果有出入,这就需要进行优化。我们可以用ADS中的Optim工具来进行多次的优化直到达到预定的设计要求。
3 设计实例
设计 指 标:中 心 频 率 f0为 2.6 GHz, 带 宽200 MHz,在f=2.8 GHz及2.4 GHz上衰减不小于40 dB,通带内纹波3 dB,输入输出特性阻抗均为50 Ω。
微带电路板的参数如下:厚度H=0.4 mm[8],介质相对介电常数为Er=3.66,相对磁导率为Mur=1,金属层厚度T=0.03 mm,损耗正切角TanD=0。
根据设计的指标及式(1)我们选用n=5 的3 dB纹波切比雪夫低通原型。查表[1]求得低通滤波器原型的原件取值为:

由式(3)得:

计算平行耦合线的W, S, L,由ADS中的Line-Calc得到。
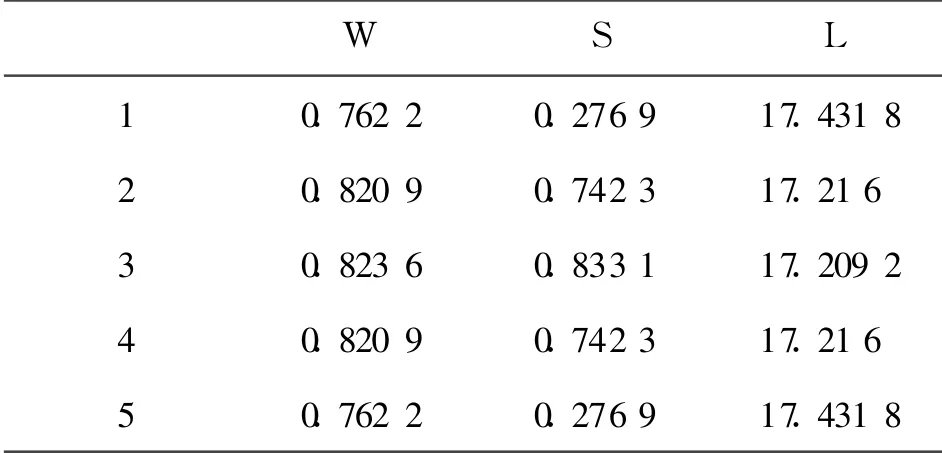
表1 各节耦合微带线的尺寸 单位:mm

图2 ADSLinecalc模块
将上述的结构尺寸输入ADS中并设置微带电路板的参数和S参数的频率扫描范围进行原理图仿真。以下图3是理论计算值的仿真原理图,图4是仿真结果。
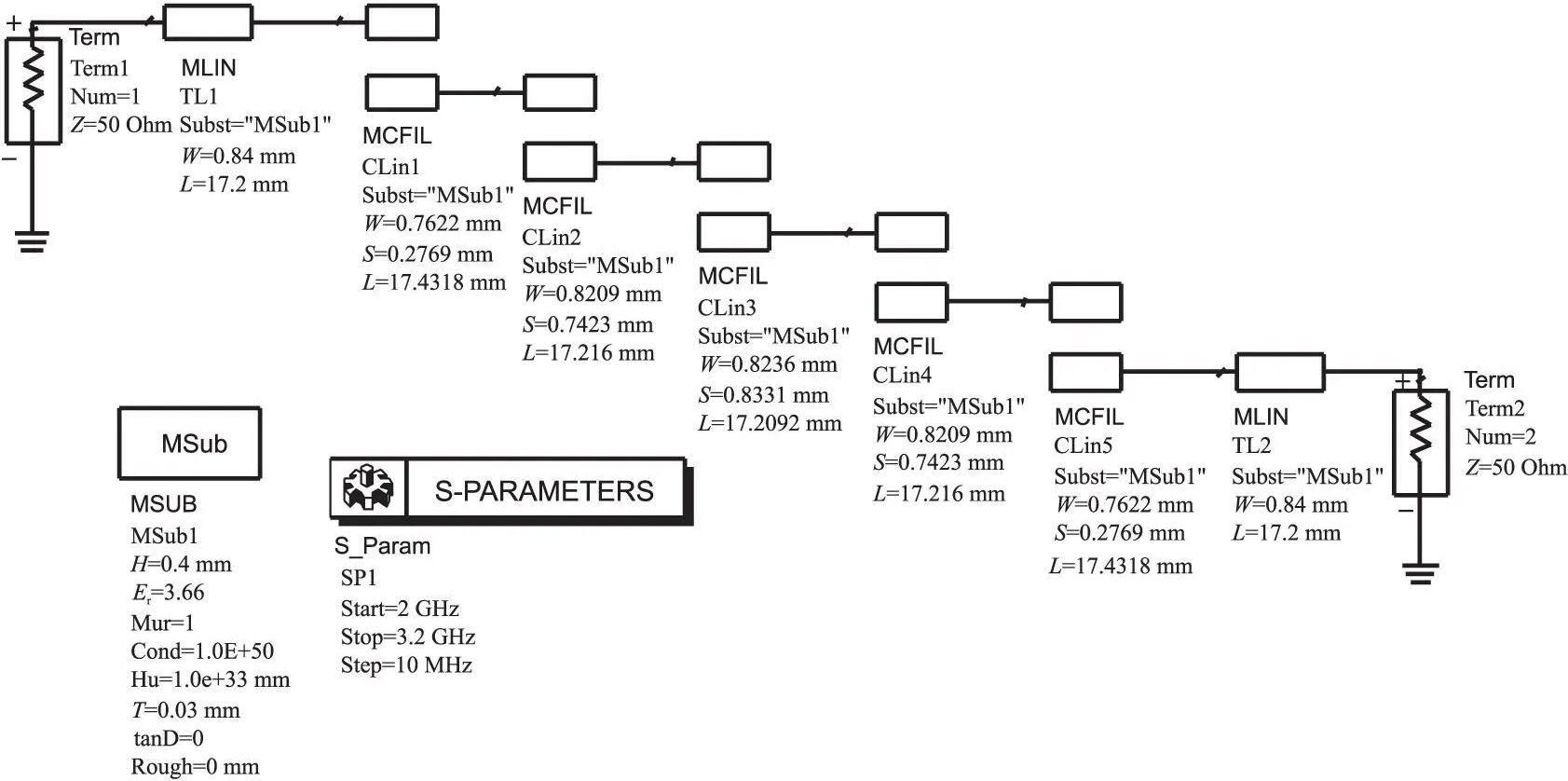
图3 微带线带通滤波器设计原理图
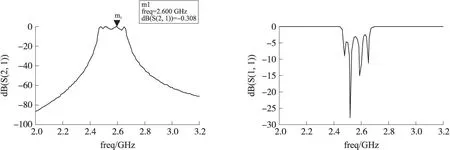
图4 传输、反射系数仿真曲线图
经过分析仿真结果出现了中心频率点偏移的,并且通带内的反射系数较大,在2.4 GHz上衰减没有达到要求,因此需要对其进行优化。优化时要注意:耦合线的W,S, L不要设为具体的值,而是要有各个变量来代替[6],因为这些参数就是优化的目标。变量的设置要需要借助变量控件VAR来完成,在VAR中要设置合理的数据范围。优化还需要Optim控件和目标控件Goal,将Optim控件中的Maxlters的值该为100,增加优化次数。根据我们的设计要求设置四个Goal控件。依次分别为:优化通带内的S(2, 1)、优化通带内的S(1, 1)(优化通带内的反射系数)、优化低端阻带内的S(2, 1)(设定2.4 GHz以下达到40 dB衰减)和优化高端阻带内的S(2, 1)(设定2.8 GHz以上衰减达到40 dB)。如果一次优化不能满足设计指标的要求,则需要再改变变量的取值范围,进行重新优化,直到满足要求为止。
图5为优化原理图,图6是优化后生成的仿真结果。由图6 中可以看到f=2.6 GHz时, S(2, 1)=-0.113 dB, f=2.8 GHz和f=2.4 GHz时衰减都大于40 dB,反射系数也比较理想,各项基本满足设计要求。
微带滤波器的实际电路是由实际电路板和微带线构成的,实际电路的性能可能会与原理图仿真的结果会有很大的差别。因此,需要在ADS中对版图进行进一步的仿真之后才能进行电路板的制作。首先我们要生成版图,由优化后的原理图生成的版图如图7所示。
接着我们对电路版图进行矩量法Momentum仿真,仿真结果如图8。由图8可以看出版图仿真得到的曲线满足指标要求。版图的仿真是采用矩量法直接对电磁场进行计算,考虑了实际因素,其结果比在原理图中仿真更加真实。
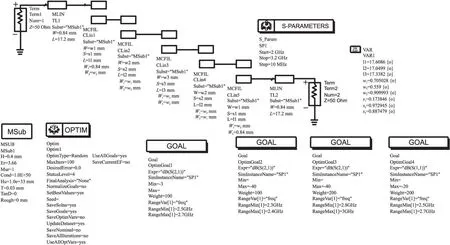
图5 微带线带通滤波器优化原理图

图6 优化后的S参数曲线图

图7 微带版图
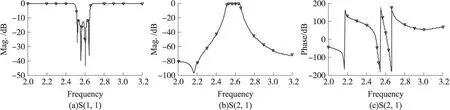
图8 微带版图仿真曲线
4 结论
本文从耦合微带线的基本理论出发,完整的阐述一种利用ADS来进行微带带通滤波器的设计方法,并设计出了一个达到预期的微带带通滤波器。利用ADS软件可以大大减少工程师的工作量,并且能提高效率,降低成本。
[ 1] 黄玉兰.射频电路理论与设计[ M].北京:人民邮电出版社,2008, 10.
[ 2] 韩持宗,朱静.基于ADS仿真设计的微带带通滤波器[ J] .电子设计应用, 2007, 9.
[ 3] 清华大学《微带电路》编写组.微带电路[M].北京:人民邮电出版社, 1975.
[ 4] 陈艳华,李朝晖,夏玮.ADS应用详解—射频电路设计与仿真[ M] .北京:人民邮电出版社, 2008, 4.
[ 5] LUDWING R.RF Circuit Design:Theory and Application[ M] .Upper Saddle River, NJ, USA:Prentice Hall, 2000.
[ 6] 钟蔚杰,杨景曙.微带线带通滤波器的ADS辅助设计[ J] .现代雷达, 2008, 3.
[ 7] 周郭飞,赵全明,腾建辅.微带电容间隙耦合传输线带通滤波器的优化设计[ J] .微波学报, 2003, 19(1):34-38.
[ 8] Rohde U L.无线应用射频微波电路设计[ M] .刘光枯,译.北京:电子工业出版社, 2004.
