两种非理想气体为工质的可逆奥托循环的效率＊

叶兴梅 刘静宜

（漳州师范学院物理与电子信息工程系，福建 漳州 363000）

两种非理想气体为工质的可逆奥托循环的效率＊

叶兴梅 刘静宜

（漳州师范学院物理与电子信息工程系，福建 漳州 363000）

分别以范德瓦耳斯气体和昂尼斯气体为工质计算奥托循环的效率.

奥托循环；非理想气体；效率

奥托循环是内燃机的一种重要循环方式之一，它是19世纪德国工程师N.A.奥托提出的，因而得名.一般热学教材［1，2］中计算奥托循环的效率都是以理想气体为工质导出η＝1－（V2/V1）γ－1.在通常的压强和温度下，可以近似地用理想气体状态方程来处理问题，但当奥托内燃机运行时其内部的压强和温度很高，此时理想气体状态方程就偏离实际情况较远，在这样的情形下，以理想气体为工质导出的热机的效率就不能很好地反映出实际热机的效率.范德瓦耳斯气体和昂尼斯气体是最具有代表性的两种非理想气体，本文分别以范德瓦耳斯气体和昂尼斯气体为工质计算可逆奥托循环的效率.

1 热力学基本理论

对于无限小的热力学过程，热力学第一定律的表示式为

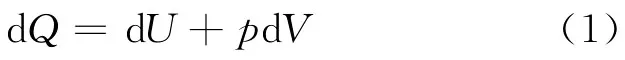
选T、V为独立变量，内能的全微分为

根据热力学理论

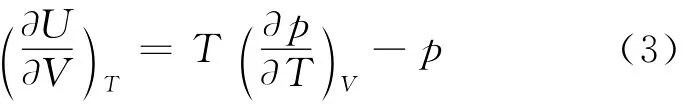
以上式（1）～（3）是基本的热力学公式，对于范德瓦尔斯和昂尼斯两种气体都适用。下面分别以范德瓦尔斯气体和昂尼斯两种气体为工质计算可逆奥托循环的效率。

2 工质为范德瓦耳斯气体

假设实际气体满足范德瓦耳斯气体方程［3］，则1mol实际气体的范氏方程为

其中，p、V和T 分别是范氏气体的压强、体积和温度；R是摩尔气体常量；a和b是两个常数.

由式（3）和式（4）可得

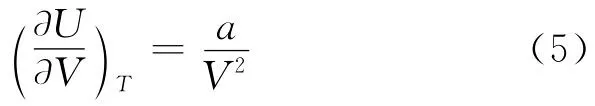
所以

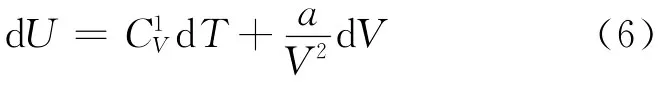
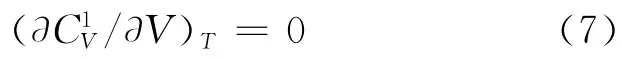
对于准静态绝热过程，dQ＝0，由式（8）可得

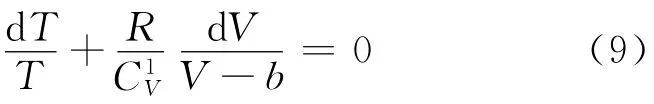
设1mol范氏气体经历一可逆奥托循环12341，如图1所示，其中1－2为等容吸热过程，2－3为绝热膨胀过程，3－4为等容放热过程，4－1为绝热压缩过程.V1、V2分别为循环中所对应的最小、最大的体积.

图1 可逆奥托循环p－V图

热机效率的定义式为

根据式（8）可得工质在两等容过程中分别吸、放热为

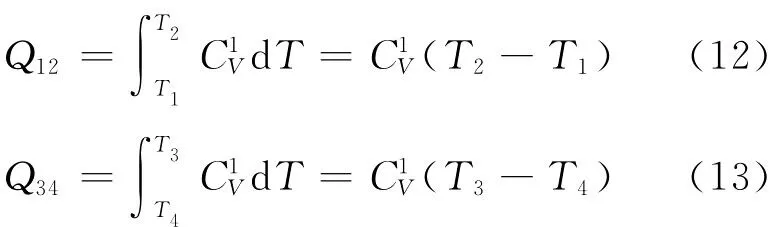
2－3和4－1为两绝热过程，根据式（10）可有

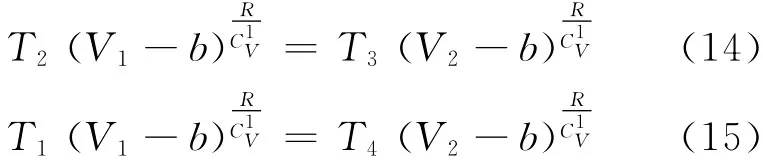
将式（12）～式（15）代入式（11），即可得到以范氏气体为工质的奥托循环的效率

当a＝0和b＝0时，范氏气体简化为理想气体，式（16）就简化为以理想气体为工质的可逆奥托循环的效率η＝1－（V2/V1）γ－1.

3 工质为昂尼斯气体

设有1mol昂尼斯气体，经历一可逆奥托循环.昂尼斯方程［3］为

式中，A、B、C、D、…分别叫做第一、第二、第三、第四、…维里系数，它们都是温度的函数，其中A＝RT，则有

由式（3）可得

所以

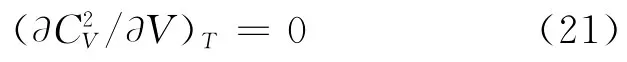
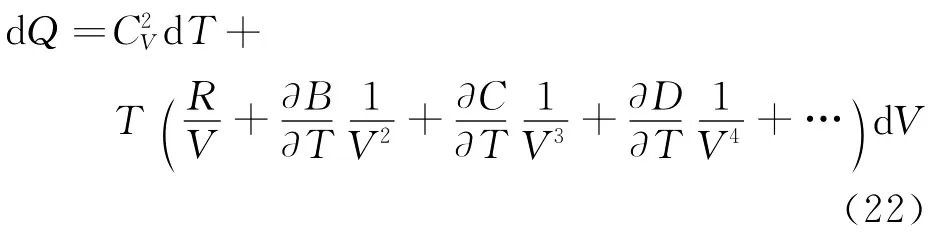
对于准静态绝热过程，dQ＝0，由式（22）可得

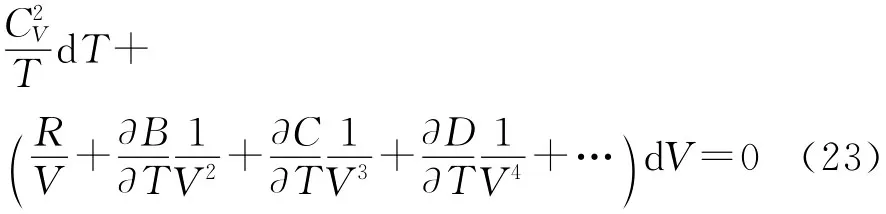
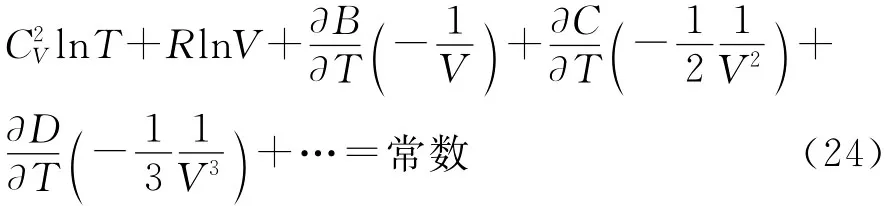
根据式（22）可得工质在两等容过程中吸、放热分别为

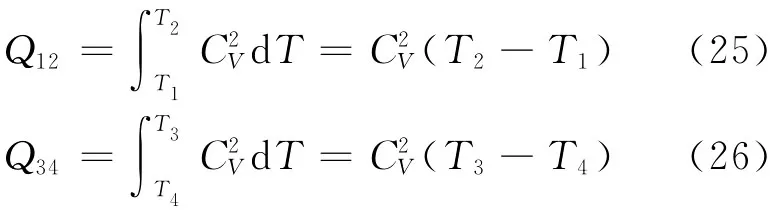
2－3和4－1为两绝热过程，根据式（24）可有

式（27）减去式（28）可得

将式（25）～（26），（28）～（29）代入式（11），即可得到以昂尼斯气体为工质的奥托循环的效率

［1］ 汪志诚.热力学·统计物理 第三版［M］.北京：高等教育出版社，2003

［2］ Zemannsky M W.Heat and Thermodynamics［M］.5th ed，New York：McGraw－Hill，1968

［3］ 李椿，章立源，钱尚武.热学［M］.北京：高等教育出版社，1978

EFFICIENCY OF THE EVERSIBLE OTTO CYCLE WITH TWO KINDS OF IMPERFECT GAS AS THE WORKING SUBSTANCE

Ye Xingmei Liu Jingyi
（Department of Physics and Electronic Information Engineering，Zhangzhou Normal College，Zhangzhou，Fujian 363000）

The efficiency of the eversible Otto cycle has been calculated by taking the van der Waals gas and the Onnes gas as the working substance，respectively.

Otto cycle；imperfect gas；efficiency

2009－07－11；

2010－04－01）

漳州师范学院科研基金资助项目（L20745）；福建省自然科学基金计划资助项目（2008J0222）；福建省教育厅科技计划项目（JA08158）.

叶兴梅（1978年出生），女，福建南平人，硕士，讲师.主要从事现代热力学及磁制冷等方面的研究.