备兑权证定价方法的务实改进与实现

祝荷君,韩士专

(华东交通大学 经济管理学院,江西 南昌 330013)

●实务·方法

备兑权证定价方法的务实改进与实现

祝荷君,韩士专

(华东交通大学 经济管理学院,江西 南昌 330013)

为使备兑权证的定价更加贴近现实,文章以 t分布代替原假设标的股票收益率服从的正态分布,以随机波动率代替历史波动率,通过 GARCH模型来消除金融时间序列的异方差性,并考虑交易费用、红利等因素对权证价格的影响,在此优化了传统的定价模型。然后用Monte Carlo模拟的定价思路,并利用对偶方差减少技术提高其效率,最后编辑程序在 Eviews中成功运行得出权证的定价。

认股权证;GARCH(1,1);Monte Carlo模拟;对偶方差减少技术

一、引 言

备兑权证多用 Black-Scholes模型或修正的 Black‐Scholes模型定价,该模型在一系列严格的假设下成立,它的主要缺点是假设过于理想化,考虑现实情况的解析解难以推导,具有局限性,并且该公式使用的波动率为常数,不符合现实情况。

文献 [1]从实证的角度检验了 Black‐ Scholes公式和蒙特卡罗模拟方法定价的效率,实证表明,蒙特卡罗方法效果很明显,它的一个优势是随着变量个数的增加,运算的时间近似为线性增长,所以它的运算是很有效率的。但是他定价时使用的是标的资产的历史波动率。标的股价作为一种金融时间序列,其波动性存在着明显的聚集性和爆发性,历史波动率无法表示这一经验现象,因而有可能导致定价的偏差。用随机波动率代替历史波动率优化定价方法,即通过GARCH模型对数据进行参数估计,能描述出数据的条件异方差性。文献 [2]应用四种权证定价模型和方法,对我国的权证的定价效果进行检验,发现标的股票收益率分布的非正态性使得Black‐ Scholes模型和蒙特卡罗模拟有效程度降低。文献 [3]探讨了有交易成本条件下的期权定价问题。文献 [4]考虑了有与股票价格成比例的交易费和股票的离散随机分红时的期权定价,但是其股票价格服从对数正态分布,波动率为常数,不符合实际。文献 [5]依据权证定价方法的发展过程及其应用特点,对近些年来国内外在这一领域所开展的主要工作及成果进行系统的分析与评述,提出在该研究领域的进一步研究方向,认为在基于随机波动率假设的基础上,能更加真实地反映权证价值的蒙特卡罗模拟等数值定价方法,将成为权证定价乃至整个金融融资资产定价的重要方法。文献 [6]研究了蒙特卡罗模拟的方差缩减技术,分别有控制变量、对偶变量、分层抽样等,他们对期权定价的模拟效率都有显著提高。

本文首先以标的股票收益的随机波动率代替历史波动率,使用 GARCH模型描述金融资产收益波动率的异方差现象和波动集聚现象,用 t分布代替正态分布描述金融时间序列的“尖峰厚尾性”。然后将交易成本、红利等因素考虑入内,用蒙特卡罗模拟对认购权证进行定价,并用对偶变量技术提高其效率,最后以中行瑞银九零八认购权证为例进行实证分析。

二、对传统认股权证定价模型的优化

(一)正态分布的检验

可以用偏度、峰度和 Jarque-Bera统计量来检验数据的正态性。偏度是用来描述分布曲线的偏斜程度的,而峰度则是用来描述分布曲线的陡缓程度的[7]。Jarque-Bera统计量(以下简称 JB统计量)用于检验序列是否服从正态分布的检验统计值 (检验对应的原假设为序列服从正态分布)。

金融市场的大量实证结果表明,对数正态分布模型并不完全与历史回报数据性质相一致,短期历史回报的分布往往是略微偏斜的,且其尾部要比正态分布更厚。本文用 t分布的概率密度函数来描述回报的厚尾特征。

(二)消除金融时间序列的异方差性

GARCH模型,即广义自回归条件异方差模型,是在ARCH的基础上发展起来的,它能够较好地描述金融资产收益波动率的异方差现象和波动集聚现象。而这一现象是权证定价中的一项重要因素。

我们将其形式限定为 GARCH (1,1)模型,Duan(1995)提出股票的收益率满足如下形式:

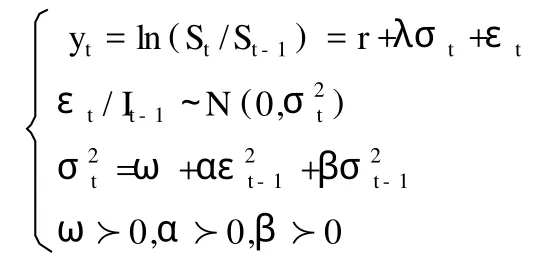
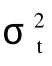
通过在方差方程中加入了残差平方和残差方差的滞后项,对金融时间序列的条件异方差性进行了有效的表达,并给出了计算条件异方差的方法。

(三)考虑红利支付的定价公式

有收益资产的收益支付一般可分为两种:按现金收益的方式支付和按收益率的方式支付,对应于不同的支付方式,欧式看涨期权的定价模型有所不同。

(四)考虑交易成本的定价公式

三、改进的备兑权证定价方法

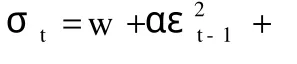
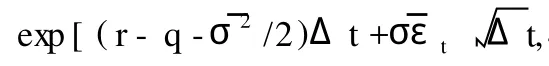
分析基础资产在到期日 T时的价格。就看涨权证而言,若到期日基础资产价格 ST≤K(K为权证执行价格),则此次重复实验下,权证价值为 0并到期作废。若 ST>K,则到期时该期权为实值期权,其在到期日的价值等于 ST-K,应使用无风险利率求出其贴现值[10]。

(3)利用命令 “Qt=-Qt”引入对偶变量,重复以上的模拟过程。将此路径下的结果存储在权证价格数组的偶数行中。求此数组中所有数值的平均值,该平均值即为所求的权证价格。

四、实证分析

在本文中,我们将以中行瑞银九零八为例进行权证定价分析,数据处理采用软件 eviews5.1。

(一)样本选取

中行瑞银九零八基本资料见表 1所列。

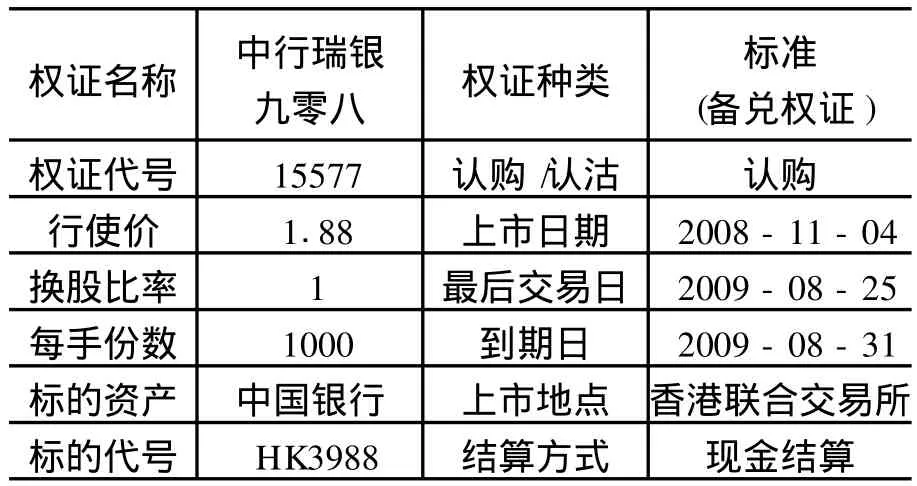
表1 中行瑞银九零八基本资料

中行瑞银九零八为欧式看涨权证,股票初始价格为 S0=2.9元,执行价格为 K=1.88元,时间步长为一小时,取无风险利率为 r=0.0096571,股票波动率为σs=0.25,交易费用比例为 k=0.01,股票息率 q=0.0405。

(二)标的资产收益率分布及随机波动率假设的实证检验

选取 2008年 11月 4日—2009年 4月 30日的中国银行每小时股票收盘价 St为样本,共 478个数据,根据所选取的样本,通过公式 Rt=log(St) -log(St-1)得到标的股票的收益率 Rt,其中 St表示 t时期标的股票的收盘价,St-1表示上一期标的股票的收盘价,对其分布特征进行研究。在传统的期权定价理论中,都是假设标的股票的收益率服从正态分布,通过 Eviews软件得到收益率分布图,如图 1所示。

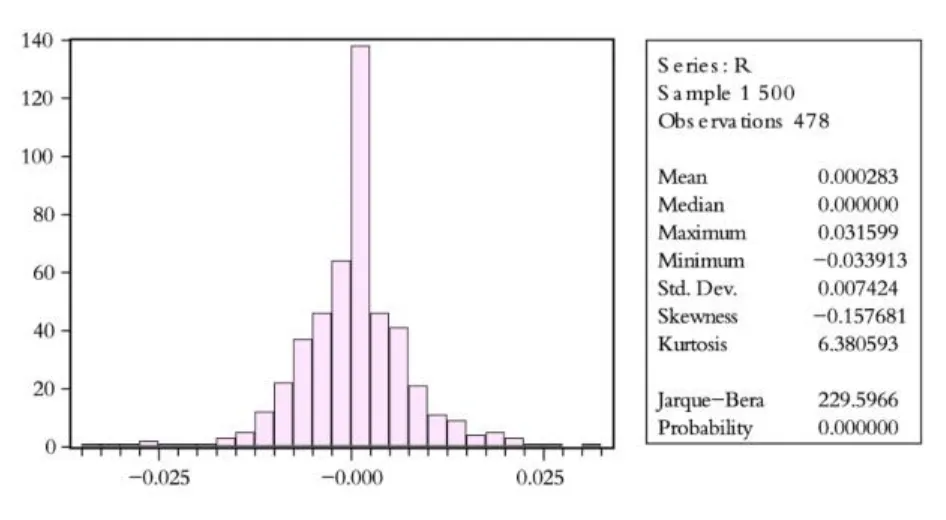
图1 中行股份收益率序列的基本统计资料

对于标的资产股票,从 2008年 11月 4日—2009年 4月3日的收益率为 0.000283,标准差为 0.007424,其偏度为 -0.157681,为负,说明序列分布有长的左拖尾;峰度为6.380593,大于正态分布的峰度 3,表明分布比较高耸,说明收益率序列具有尖峰厚尾的特征;Jarque-Bera统计量显示拒绝正态分布的原假设,对数收益率尖峰厚尾特征明显。

对于标的股票收益率波动的研究,采用 GARCH(1,1)模型为分析工具,残差服从标准化学生 t分布的估计结果见表 2所列:

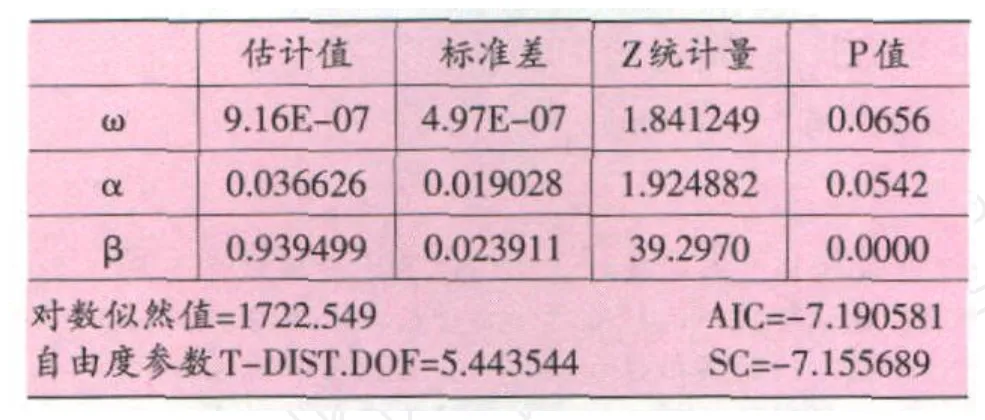
表2 GARCH(1,1)模型参数估计结果

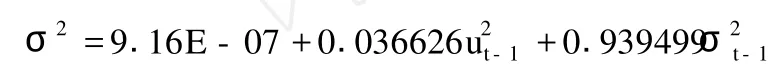
对该 GARCH(1,1)模型的方差方程的残差序列在滞后阶数等于 6时,异方差的ARCH LM检验的统计结果见表 3所列。

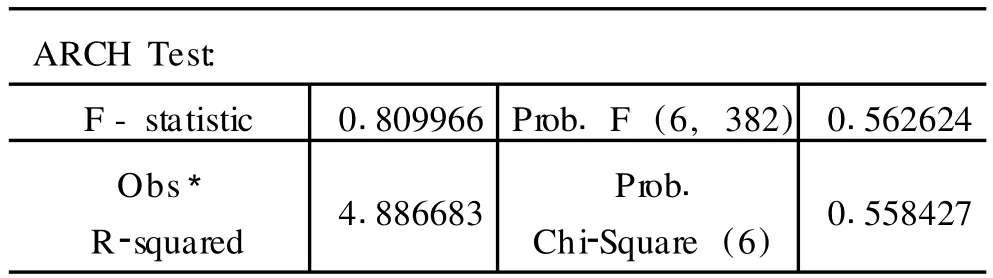
表3 GARCH模型的ARCH-LM检验结果

结果显示:LM统计量的值为 4.886683,尾概率为0.558427,接受原假设,认为残差序列不存在 ARCH效应,说明利用 GARCH(1,1)模型消除了残差序列的条件异方差性。

(三)蒙特卡罗模拟期权价值

认股权证标的股票收益率服从学生 t分布的 GARCH(1,1)波动率模型的蒙特卡罗模拟过程如下:

(1)确定模拟的步数及路径总数,权证到期时间为 0.32年,设步数为 10000,路径总数为 10000。

(2)创建服从 t分布的随机矩阵 RANDS=@RTD IST(5.443544),从 GARCH过程中生成随机样本。

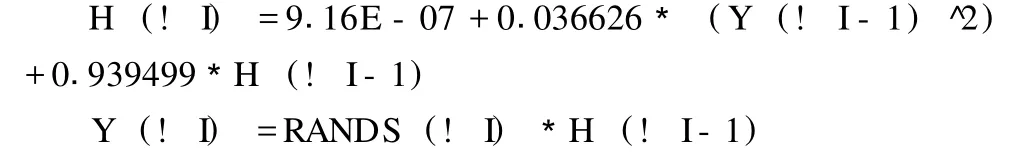
分析基础资产在到期日 T时的价格。就看涨权证而言,若到期日基础资产价格 ST≤K,则此次重复实验下,权证价值为 0并到期作废。若 ST>K,则到期时该权证为实值期权,其在到期日的价值等于 ST-K,应使用无风险利率求出其贴现值。

(4)重复 (2)和 (3)共 10000次,并对 10000次重复实验得到的期权价格取平均值,即为所求的期权价格。

(5)利用命令 “RANDS=-RANDS”引入对偶变量,在重复以上的模拟过程。此路径下的权证价格存储在数组ACVAL的偶数行中。

(四)模型结果比较分析

在 Eviews中运行所编辑的程序,得出 CALLPR ICE=0.96776,即为该权证定价 0.96776元。权证实际价格为0.96元,将传统定价方法与改进后的方法进行比较,结果见表 4所列,可以看出,务实改进后得出的结果更为精确。

表4 定价方法的比较

五、结束语

通过股票价格模式的改变及放宽条件,并且将对偶变量技术应用于Monte Carlo模拟过程中,得到了更精确和符合现实证券市场的期权价格模型。计算出的价格可用来作为评价权证是否有投资价值的一个标准,通常理论价格高于市场价格的权证较具有投资价值。

[1]郭雪,葛翔宇.蒙特卡罗方法在权证估价中的应用[J].经济师,2007,(3):25-26.

[2]侯迎春,门明.我国股本权证定价效果的实证研究[J].金融与经济,2008,(7):41-45.

[3]郑小迎,陈金贤.有交易成本的期权定价研究 [J].管理工程学报,2001,(3):35-38.

[4]吴永红,蹇明,叶小青.有交易费和随机分红时的欧式期权定价 [J].华中科技大学学报 (自然科学版),2005,(6):123-124.

[5]王彦,马俊海.权证定价理论方法的发展过程及未来研究展望 [J].河南金融管理干部学院学报,2008,(3):22-29.

[6]陈辉.期权定价的蒙特卡罗模拟方差缩减技术研究[J].统计与信息论坛,2008,(7):86-96.

[7]张晓峒.计量经济学软件 Eviews使用指南 [M].天津:南开大学出版社,2004:12.

[8]GuyBarles,HalilMete Soner.Option pricing with transation costs and a nonlinear Black-Scholes equation[J].Finance Stochast,1998,(2):369-397.

[9]张鸿雁,胡常乐,李学全.基于中国股权结构的认股权证定价模型 [J].统计与决策,2009,(2):140-141.

[10]Paul Glasserman.Monte Carlo Methods in Financial Engineering[M].Springer,2005:7.

Practical I mprovement and I mplementation of theWarrants Pricing

ZHU He-jun,HAN Shi-zhuan
(School of Econom ic and M anagem ent,East China Jiao Tong University,Nanchang330013,China)

Tomakewarrantspricing closer to reality,in thispaper,distribution replaced the original assumption that the yield of the underlying stock follows the log-normal probability distribution,historical volatility is replaced by stochastic volatility,GARCH model adopted to eliminate the financial time series heteroscedasticity,and take into account transaction cost which affect the price of the warrants,in this case,we optimize the traditional models. Then usingMonte Carlo simulation and the variance reeducation techniques of antithetic variates to improve its efficiency,finally,editing program and run in Eviews pricingwarrants successfully.

warrant;GARCH (1,1);Monte Carlo simulation;antithetic variates

F271

A

1007—5097(2010)12—0143—03

10.3969/j.issn.1007-5097.2010.12.036

2009—05—23

祝荷君 (1986—),女,湖北鄂州人,硕士研究生,研究方向:金融工程;韩士专 (1963—),男,江苏宿迁人,副院长,教授,硕士生导师,博士,研究方向:金融工程,财务会计,知识产权。

[责任编辑:余志虎 ]