债务抵押契约模型市场重构与违约损失率分布

徐承龙,徐晓芸

(同济大学 数学系, 上海200092)

债务抵押契约, 又称债务抵押证券(collateralized debt obligation,CDO), 是一种信用衍生产品, 是近年来发展最快的证券化产品之一.CDO 是以抵押债务信用为基础, 基于各种资产证券化技术, 对债券、贷款等资产进行结构重组, 重新分割投资回报和风险, 以满足不同投资者需要的创新性衍生证券产品.

由于一般CDO 的资产池涉及到100 —200 个资产, 其定价有较大的困难,现在业界比较通用的就是高斯-Copula 模型.在高斯-Copula 模型中, 影响公司违约的因素(称之为资产指标)被分成了2 个部分——系统因子部分和特异因子影响部分, 且系统因子与特异因子都是高斯分布.高斯-Copula 模型结构比较简单清晰,应用于CDO 定价时易于处理分析, 而且计算效率高.然而高斯-Copula 模型也有非常明显的缺点:该模型各个债务对象之间的违约发生是正态的,不具有偏态性.而按照对金融市场的观察,各个债务对象之间, 在不同经济形势下, 违约相关性具有明显的差异.一般来说, 经济形势较好时, 违约发生的相关性较小;而经济形势较差时, 违约的相关性要高得多.

之后的很多CDO 定价模型都是在高斯-Copula 模型基础上衍生而来的.O' Kane 等[1]根据多年对市场复合CDO 数据的研究提出了一个基于单因子高斯-Copula 的LHP(large homogeneous portfo lio)模型.O' Kane 等[2]对LHP 模型中系统因子的正态假设做了修改, 引入T-Copula;Anna Kalemanova 等[3]提出了系统因子.分布的LHP 模型;Leif Andersen 等[4]提出了2 个拓展方案来克服高斯-Copula 模型的缺点:一是引入经过随机化处理的回收率, 使回收率与违约概率具有明确的负相关性;二是将债务对象的系统因子前的系数换成与当时经济情况有关的随机变量,使得模型在经济形势较差时违约发生的可能性明显高于经济较好的情形.以上的这一类CDO 定价模型有一个基本框架:从债务对象的资产指标和违约损失率(LGD)的分布,分析出CDO 损失分布,进而给出CDO 每个分层的现金流分布,以及CDO 各分层定价模型.

上面提到的LGD ,是指预期违约的损失占风险暴露的百分比.它是信用风险和信用风险管理研究的重要课题之一.同时LGD 也是巴塞尔新资本协议内部评级法(IRB)规定的风险要素之一.Frye[5]研究发现:当宏观经济市场变差时, 会同时导致违约概率的上升和回收率(recovery)减小, LGD 增大.A ltman等[6] 也得出了同样的结论.

基于广义的高斯-Copula 框架, 本文在文献[7] 方法的基础上, 在回收率是随机的假设下, 研究了相应的系统因子的重构问题.即预先并不给定系统因子的分布,而是由市场CDO 报价来决定系统因子的分布形式.由于市场信息的缺乏, 要完全重构系统违约因子的分布函数较困难, 而用最小相对熵原则就可以从所有满足条件的分布中, 得出最佳的、最合理的分布.其主要想法是:满足所给的部分市场信息,如果一个概率密度函数能使之对于给定的先验概率密度函数的相对熵最小, 就表示这是最佳的概率密度函数.

由于该模型各个分层的现金流函数含有待定的系统因子的分布函数, 这不是标准的最小相对熵问题.本文用迭代的方法将非标准问题转化为标准的最小相对熵问题, 进行重构问题的求解, 得到系统因子的密度函数.数值计算表明, 算法是稳定和收敛的.从而由系统因子与LGD 的关系,就得到市场预期的LGD 分布.结果表明, LGD 分布能较好地反映金融市场的实际状态.

1 CDO 定价模型框架

下面先介绍CDO 定价模型框架的结构,其主要的想法来自于文献[4] .

考虑一个共有N个债务对象的CDO,其保费支付时刻为t1,…,t K.它的潜在损失可以分为:[D0,D1), …,[DJ-1 ,D J), 称之为分层1,…, 分层J(通常可认为D0=0 ,J=5).设其第i个债务对象在t时刻前发生违约的概率为p i,t=pi(t)(i=1 ,2 ,3,…,N),它在违约发生时的损失为l i(本文假设是随机变量),假定li是有界的,即存在l i,max∈R+, 使l i∈[0 ,l i,max] .如果引入回收率R i,即

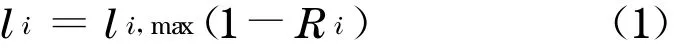
其中R i的取值范围在[0,1],回收率也可能是随机的, 则在[0 ,t] ,该CDO的全部损失为

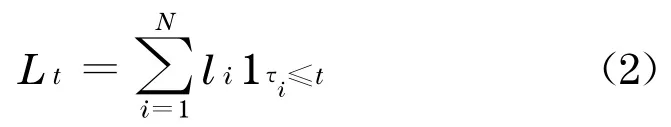
式(2)中示性函数1τi≤T表示第i个债务对象在t时刻前发生违约时取1 ,否则为0 .而CDO的期望损失为

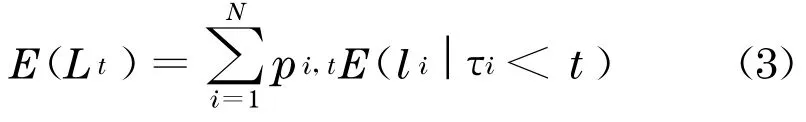
为更进一步研究违约损失分布的特性, 假定存在连续随机变量X1,…,X N(通常表示公司的资产等指标)和固定的违约门槛c1 ,t,…,c N,t,满足条件

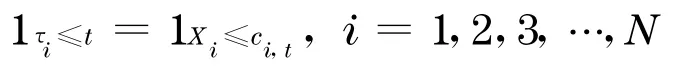
一般情况下,可以把X i和c i,t理解为债务对象i的资产指标(用于描述债务对象的资产状态)和它相应资产的违约门槛, 就如同Merton 的结构化模型所用的那样.

若记连续型随机变量X i的分布函数为F i,X,则有

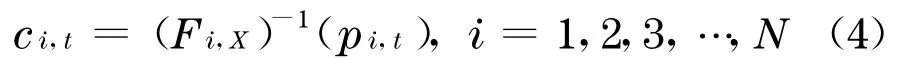
假定存在d维随机变量Z=(Z1,…,Z d), 使得在取定Z的条件下, 随机变量X1,…,X N和l1,…,l N都是相互独立的,称随机变量Z为系统因子.

在给定系统因子Z的条件下, 记债务对象i直到t时刻的违约概率为

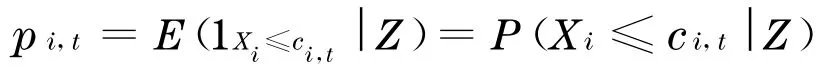
其违约时损失部分为

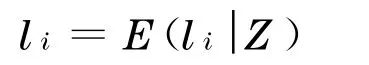
则这时的期望损失为

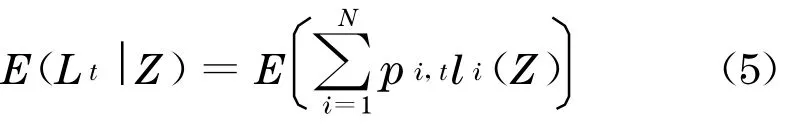
通常系统因子Z可以认为是行业或总体经济数据, 它给出了CDO投资组合的系统信用风险.

在固定时刻t,在给定系统因子Z的情形下,CDO 的分层j(j=1,2,…,J)的损失为

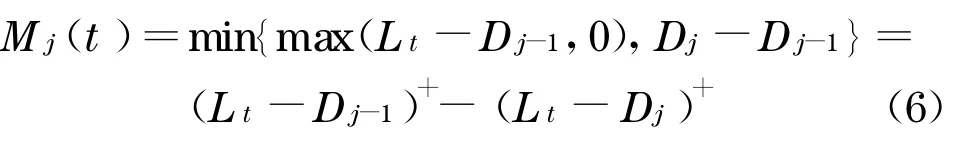
在保费支付时刻t k,分层j预期的剩余部分比率为

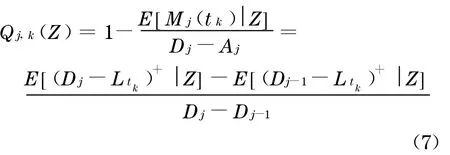
贴现到0 时刻,分层j的现金流函数的值为

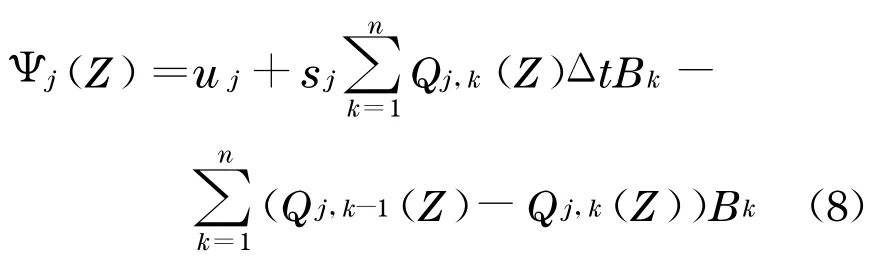
式中:u j表示预付额;s j为分层j的保费;Δt为保费的支付间隔;B k表示t k时刻的无风险贴现因子.而的意义是:到期日分层j所需要

由公平性原则, 对于所有分层(j=1 ,2,…,J),在期望意义下保费的全部支付应该等于该分层期望损失的赔付, 即

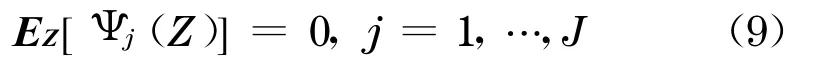
在此框架之下,只需给出X i和R i的具体模型,就得到了每一层完整的现金流函数表达式(8), 也就确定了该CDO定价模型.

下面在高斯-Copula 的基础上, 引进Frye[5]的结构模型想法及随机化的回收率模型, 并且系统因子Z不再是简单的高斯分布, 而是拓展为一个一般的d维的分布, 即

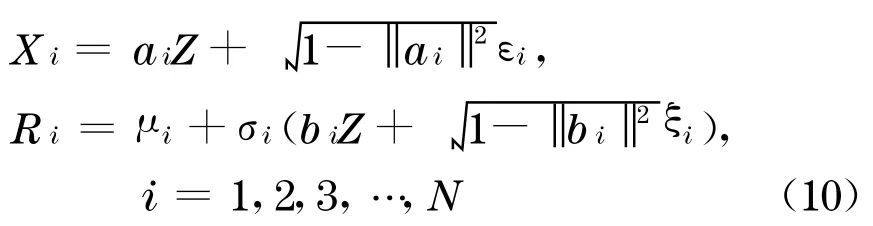
式中:a i是d维非负向量;b i是d维向量(i=1,2 ,3,…,N),它们的长度小于1 ;特异因子εi是一组相互独立的标准正态随机变量, 与系统因子Z也是相互独立的;ξi也是一组标准正态随机变量,它与系统因子Z以及所有的特异因子εi(i=1 ,2 ,3,…,N)都是相互独立的;μi,σi是定常值.

这里的回收率R i也分成系统因子影响因素σi b i Z和特异因子影响因素之 和.注意到R i与X i受到同一个系统因子Z的影响, 因此,可以直接通过控制系统因子Z的2 组系数a i和b i来调整违约概率与回收率之间的相互依赖关系.对于债务对象i和j(i,j=1,…,N),如果有a i b j=0,则表示X i的违约与回收率R j是相互独立的.

引理1 设系统因子Z的概率分布密度为ω(z),Fi为X i的概率分布函数, 则违约门槛

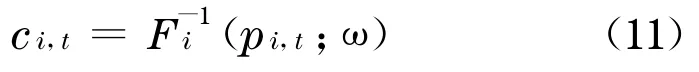
证明

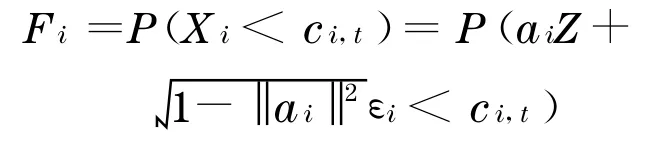
由于假设Z和εi是互相独立的, 立得

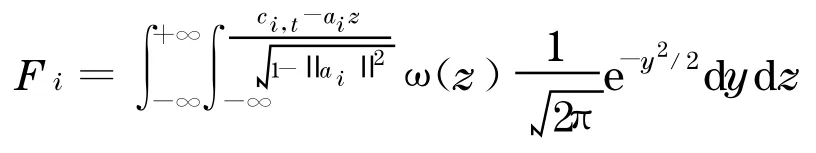
2 重构模型的计算分析

在实际市场中,系统因子Z的分布是一个重要的金融因素, 然而它的分布却是未知的.因此这里的模型远远比高斯-Coup la 模型要复杂, 并且违约门槛的大小还与未知的系统因子分布有关.根据随机化回收率的模型, 把系统因子Z看作是某种能够服从市场条件报价的未知分布, 而将高斯分布作为它的先验分布, 具体的分布函数应该依赖于当前人们对市场未来一段时间的预期.由于已知信息的不完全, 本节用最小熵原则以及市场上CDO 分层产品的公开报价,确定系统因子Z的分布函数.其基本原理为:将随机化回收率结构式(10)应用于CDO 定价模型框架, 就能得到各个分层的现金流函数式(8), 而市场上的CDO 报价应用于式(9), 就得到了最小熵问题的约束条件.只是这里的最小熵优化问题不是标准的最小相对熵问题,因此需要用迭代方法求解,才能得出系统因子概率密度ω(z).

为了简化计算表达,假定资产池具有一致性, 即具有相同的违约结构, 且每个资产具有相同的份额.令ρ=ai,q=bi,σ=σi.此时,在[0 ,t] 之间CDO 的全部损失为

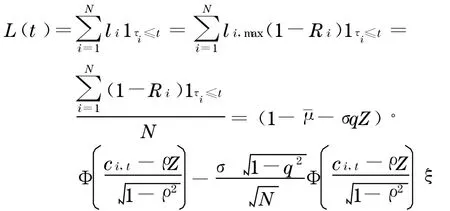
其中

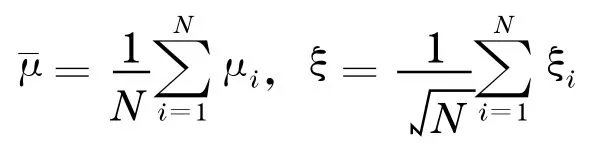
是标准正态分布的随机变量, 违约门槛ci,t的表达式

由引理1 得到,ci,t的大小与系统因子Z的密度函数形式有关.为了简化符号,记

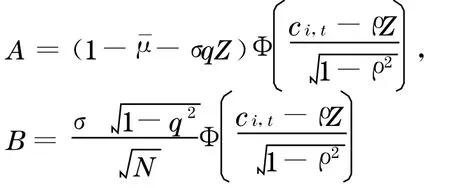
则

这里由于ci,t的关系,A,B的值与系统因子Z的分布有关.

资产池在分层j(分层j的损失范围为的损失为

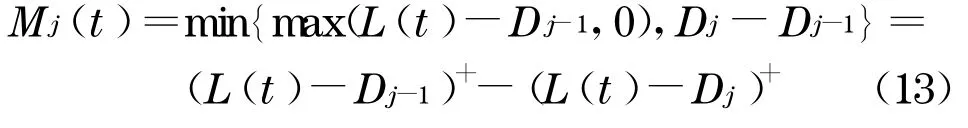
那么,在tk时刻, 分层j预期的剩余部分比率为

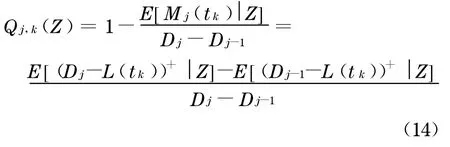
为了计算式(14), 将式(12)代入可以得到

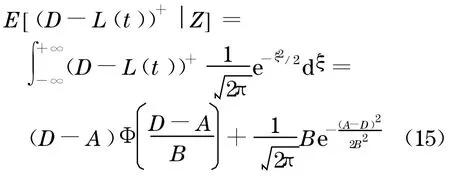
由式(15),可以计算出每一Qj,k(Z)的表达式, 将该式代入式(8),就得到分层j的现金流函数Ψj(Z),这里Ψj(Z)与系统因子的密度函数ω有关.

若能从CDO 市场得到当日的报价信息,就能根据该报价确定现金流函数和它所显示的系统因子Z的分布信息.不过,由于这是一些不完全的信息, 不能用这些信息完全给出系统因子的分布.而用最小相对熵方法, 找出一个相对最佳的未知分布.

由以上分析, 得到了CDO 模型重构的最小相对熵问题

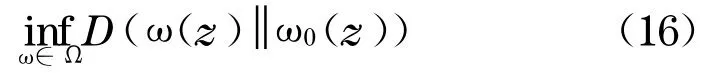
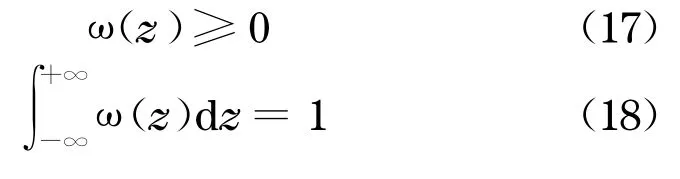
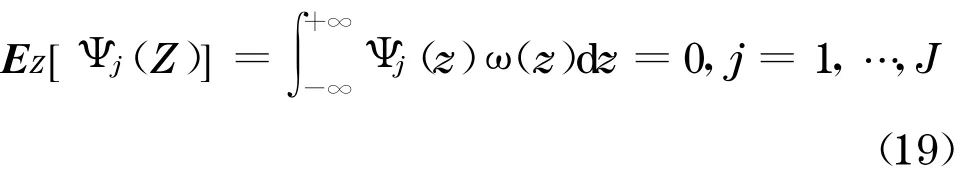
由于此时Ψj(Z)与待定的概率密度函数ω(z)有关,这个问题也不能简单地直接求解.采用迭代方法处理这一问题, 即每次求解标准最小熵问题

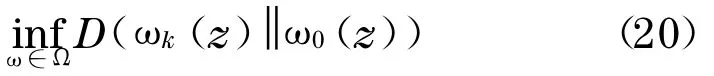
其中ci,k,t是通过求解下列非线性方程

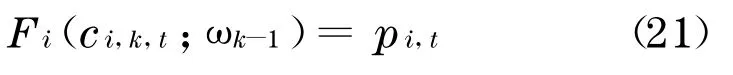
得到的.求解问题(20), 得到迭代解ωk(z)的函数形式为

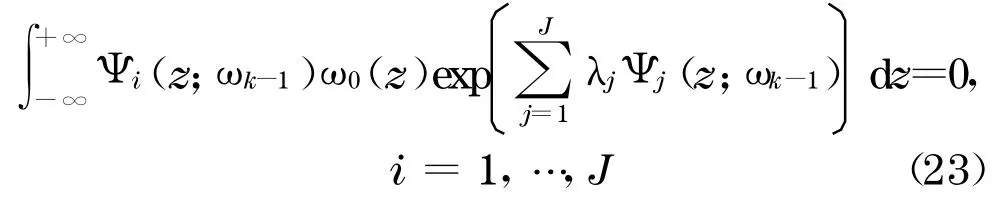
具体求解步骤为:①根据上一轮迭代得到的概率密度函数ωk-1,求解问题(21), 计算出ci,k,t;②将ci,k,t代入方程组(23), 计算出待定系数λ=(λ1,…,λJ);③将系数λ=(λ1,…, λJ)与c i,k,t代入式(22),得到概率密度函数ωk(x).

3 市场LGD 分布

一旦系统因子的概率密度函数ω(z)得到以后,就能够推出此时的市场LGD 分布了.由于所有的参数数据都是基于整个市场的总体数据, 计算分析的所有假设也都是基于总体市场的,所以得到的回收率概率分布也应该是适应于整个CDO 所覆盖的债务对象市场, 而不是其中某一个债务对象的.根据本文CDO 模型中回收率R i的形式(10),可得到CDO所反映的总体市场的回收率R为

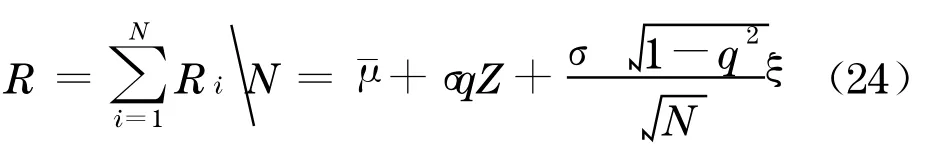
由总体市场的回收率的表达式(24), 就可以给出市场LGD 的概率分布函数G(h)

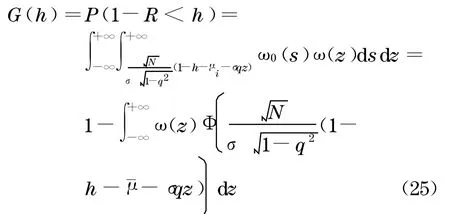
由此得到市场LGD 的概率密度函数f(h)为

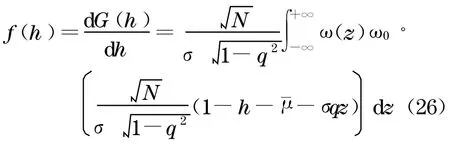
4 数值计算例子

下面基于以上对随机回收率模型(10)的计算分析,利用CDO 市场报价,给出经过最小相对熵方法的重构的系统因子的分布和相对应的市场LGD 分布.

对于最小熵模型(16)—(19), 给定其中的各个参数:ρ=0 .23 ,q=0 .17 ,σ=0 .32,=0 .41(此处参考了文献[4] 中给出的参数), 无风险利率r取1 年期的美元Libor(伦敦银行拆放利率)r=4 .233 7 %.

采用了iTraxx Eur 的CDO 市场报价,该iTraxx将在2013 年12 月20 日到期.iTraxx 包括125 家公司的CDS, 共有5 个层次报价(Tranches), 即N=125 ,J=5 .将iTraxx Eur S6 的市场报价(表1)代入式(22),(23), 并假设初始系统分布ω0 (z)=ω(z)为正态分布, 利用引理1,计算得初始的p i,t,从而计算得到ω1(z)(图1).

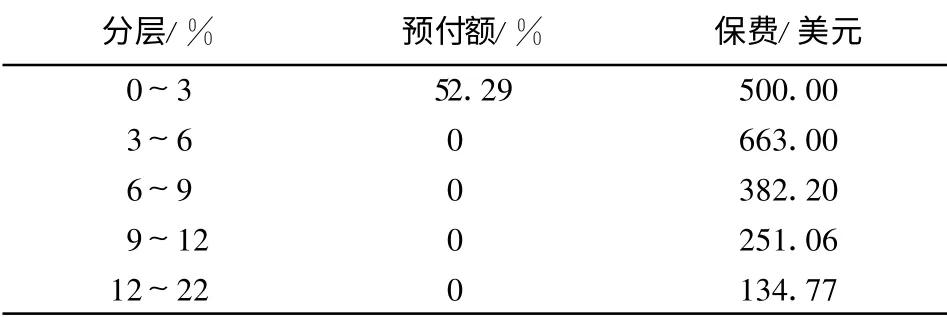
表1 iTraxx Eu r S6 的7年期在2008 年3 月21 日的报价Tab.1 Prices of 7-year-iTax Eur S6 on March 21, 2008

重复这一步骤,可看到经过每一次迭代之后, 概率密度函数的误差确实在逐步减小趋于0 .经过10次迭代, 直到最后得到满足市场报价条件的Z的概率密度函数图像(图2).

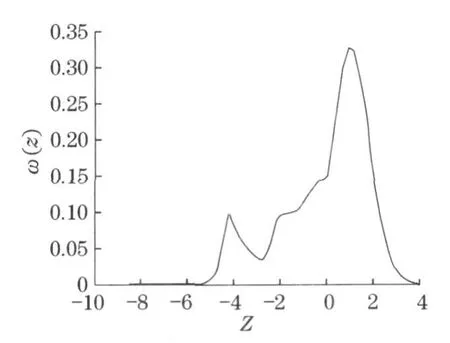
图2 系统因子10 次迭代的密度函数ω(z)Fig .2 Density function ω(z)by 10 iterations

由于相对熵基本可以看作是概率密度函数之间的一种“距离”,这里还将相对熵作为考察2 个概率密度函数偏差大小的度量, 得到了迭代次数与2 次迭代的系统因子的密度函数之间的相对偏差关系图像(图3).可以看到,相对偏差随着迭代次数的增加,很快减小趋于0 .

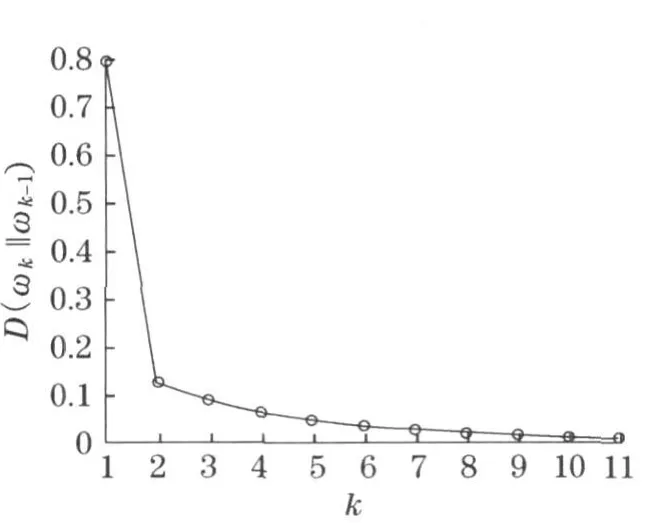
图3 迭代所得的密度函数的相对偏差D(ωk ωk-1)Fig .3 Relative error D(ωk ωk-1)of density function

由系统因子Z的概率密度函数ω(z),再由表达式(28), 就得到最终所需的市场LGD 的概率密度函数f(h)的图像(图4).

另一个例子用2007 年3 月21 日的iTraxx Eur市场报价(表2), 该iTraxx 仍将在2013 年12 月20日到期.计算得到市场LGD 的概率密度函数f(h)的图像(图5).

从上面得到的系统因子Z的概率密度函数ω(z)和市场LGD 的概率密度函数f(h)的2 个例子的图像, 可以看到,得到的结果确实能体现模型的偏态的相关性.

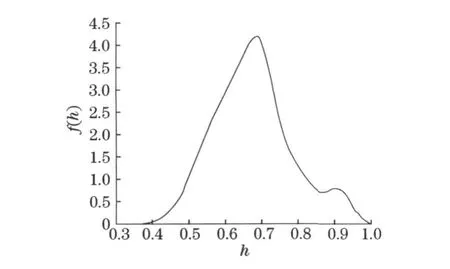
图4 LGD 的密度函数f(h)Fig.4 Density function of LGD f(h)

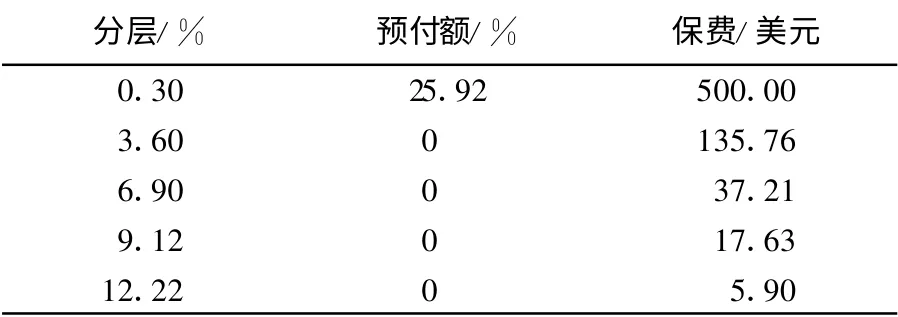
表2 iTraxx Eu r S6 的7年期在2007 年3 月21 日的报价Tab.2 Prices of 7-year-iTrax Eur S6 on March 21, 2007

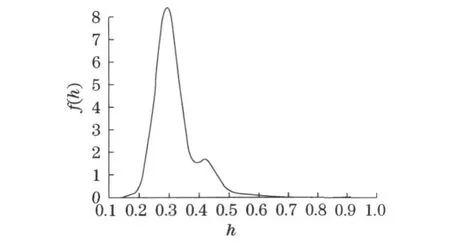
图5 LGD 的概率密度函数f(h)Fig .5 Probability density function f(h)of LGD

比较2008 年3 月与2007 年3 月的市场预期LGD 的概率密度函数图像,从2007 年3 月21 日报价给出的市场预期的违约损失率LGD 要远小于由2008年3 月21 日报价得到的市场预期LGD .2007 年3 月的市场预期LGD 取0～0 .4 的概率明显较大,而2008年3 月的市场预期LGD 大于等于0 .5 的概率要大得多.从中可以读出:2008 年3 月时,金融市场情绪比较悲观,市场预期将来一段时间内违约发生时, 损失率会非常高;而2007 年3 月的市场预期要积极得多.

5 结语

本文采用的随机化回收率模型中的回收率与高斯-Copula 模型不同, 不再是常数, 而是具有随机性的.市场形势变化时, 违约发生的概率与LGD 的大小发生同向变化.

本文首先讨论了LGD 的模型结构, 其中回收率也同资产指标一样, 将回收率的随机部分分成系统因子影响部分与每一个回收率的特异随机因子.而每一个债务对象的回收率与资产指标用的是同一个系统因子,以此体现LGD 与违约发生概率同时被市场所影响.通过系统因子Z之前的系数,体现了回收率与违约发生的相关性的大小.

目前较为常用的高斯-Copula 模型缺点是:债务对象之间的违约发生的相关性不会发生变化, 也就是各个债务对象之间的相关性应当是有偏的.Andersen[4]的随机化回收率的模型, 则由特异因子的变化来考虑;而本文随机化回收率的模型从系统因子的角度可克服这一问题, 其资产指标的系统因子的分布并不一定是高斯分布, 而是由市场CDO 报价重构系统因子的分布来确定.

用最小相对熵方法重构能够匹配CDO 市场价格的系统因子分布.这时的现金流函数也包含待定的系统因子分布, 为了求解问题的方便, 使用了迭代最小相对熵的方法, 每次为一个标准的最小相对熵问题以方便数值求解.

根据系统因子与LGD 的关系式,分析出预期未来市场LGD 的概率密度函数, 这个LGD 概率密度函数由系统因子的分布来决定.而用2007 年和2008年3 月的iTraxx Eur 报价,分布得到的预期的LGD分布图像能够较好地反映出当时的金融市场状态.

最后应该注意到, 本文的模型是静态模型, 针对CDO 框架来说, 都是从当前时刻(CDO 报价当日)起, 假定在未来一段时间内(在CDO 的到期日之前),债务对象的违约和回收率的分布结构不随时间变化而调整, 违约和回收率的分布是固定不变的.

[1] O' Kane D,Livesey M.Base correlation explained[E B/ OL] .[2009-04-20] .http:∥www.mfa-2010.com .

[2] O' Kane D, Schloegll.A note on the large hom ogeneous portfolio approximation with the student copu la[J] .Finance and Stochastics, 2005, 9(4):577.

[3] Kalemanova A,Schmidy B,W ernerz R.T he normal inverse Gaussian distribution for synthetic CDO pricing[J] .Jou rnal of Derivatives, 2007, 14(3):80.

[4] Andersen L, Sidenius J.Extensions to the gaussian copula :random recovery and random factor loading s[J] .Journal of Credit Risk, 2004, 1(1):29.

[5] Frye J.Depressing recoveries[J] .Risk,2000, 13(10):108.

[6] A ltman E,Brady B,Resti A,et al .The link between default and recovery rates:theory,empirical eviden ce and implications[J] .Journal of Business,2005, 78(6):2203.

[7] Meyer-Dautrich S, Wagner C J.Minimum-entropy calibration of CDO tranches[EB/OL] .[2009-05-10] .http:∥citeseerx .ist .psu.edu.