基于改进支持向量机的作物叶水势软测量建模
2010-12-23顾幸生卢胜利
顾幸生 ,潘 晔 ,卢胜利
(1.华东理工大学 自动化研究所, 上海200237;2.天津工程师范学院 自动化工程系, 天津300222)
精细农业(precision agriculture,PA)是21 世纪农业的重要特征,连续自动获取农田水势信息是实践精细农业的重要技术基础之一, 对发展节水高效型农业意义重大[1].到目前为止, 国内外在农田水势测量方面取得的研究成果已经很多, 其中大气水势自动监测技术已发展得较为成熟,而对土壤水势和作物叶水势的检测仍以人工测定为主.要想对土壤水势和作物叶水势信息进行连续自动检测还需要进行深入的研究,这是亟需解决的一个技术瓶颈问题[2].
软测量技术主要用来连续自动测量某些关键过程参数.农业生产系统是一个复杂的生态系统, 研究的主要对象是农作物.在这个系统中, 作物叶水势信息是非常关键的过程参数.因此成功地应用软测量技术来获取作物叶水势信息是非常有意义的.
针对作物叶水势在线实时测量比较困难的特点,本文在标准最小二乘支持向量机(least square support vector machine, LS-SVM)的基础上, 利用改进的粒子群算法(improved particle swarm optimi-zation ,IPSO)来优化LS-SVM模型参数,提出了基于IPSO-LS-SVM的软测量建模方法, 建立了作物叶水势软测量模型,并给出了相应的结果和性能比较.
1 农田水势信息
1.1 土壤—植物—大气连续体的概念
1966 年著名水文与土壤物理学家Philip 提出了土壤—植物—大气连续体(soil-plant-atmosphere continuum ,SPAC)的概念[3].在这一连续体中水分在土壤、植物和大气中的传输是研究的核心内容.
1.1 .1 大气水势
大气水势与环境温度和相对湿度之间存在明确的函数关系, 可以采用下式计算:

式中:Ψa 为大气水势;T为热力学温度, K ;Rh 为空气相对湿度, %.由式(1)可知, 大气水势在作物不同生育期由于天气条件(气温、相对湿度等)变化而发生变化.
1.1.2 土壤水势
土壤水分的多少直接关系着作物的生长, 同时它也是评价土壤是否干旱的一个重要指标.土壤水势越高,越有利于植物吸收利用土壤水分;反之, 土壤水势越低, 越不利于植物吸收利用土壤水分.土壤水势主要由土壤的含水量决定.
目前测定土壤水势的方法主要有张力法、湿度法、平衡法和露点法.其中张力法是目前应用最广泛的土壤水势测量方法.
1.1.3 作物叶水势
作物叶水势是指作物叶子细胞液中水分子的能量水平,它对植物缺水具有较为明显的表现.影响作物叶水势变化有3 大因素, 即土壤因素、作物因素和大气因素.具体是指土壤水分、土壤温度、作物生育阶段、作物生育指标、光辐射、大气湿度、CO2浓度、大气温度等[4].
作物叶水势的传统检测方法是压力室法, 但是在测量上很不方便.目前,国外已生产出可实地测量作物叶水势和土壤水势的设备, 但价格较昂贵.因此,可以通过软测量建模方法, 由作物微环境信息来推测作物叶水势.
1.2 微环境信息
定义活体作物周围的可测信息为微环境信息.将活体作物放置于如图1 所示的顶部开放植物生长室(OTC)内.这样既能减弱大气环境对作物的影响,又能使作物的生长环境尽可能地接近自然环境.顶部开放植物生长室中作物的微环境信息(温度、相对湿度、CO2体积分数)的日变化曲线如图2 所示.在活体作物周围安置传感器以检测相关信息, 作为软测量的辅助变量.

图1 微环境信息示意图Fig .1 Schematic diagram of m icro-environment information

图2 微环境信息日变化曲线Fig .2 Diurnal variation curve of m icro-environment in formation
2 最小二乘支持向量机
LS-SV M算法是一种改进的支持向量机算法[5] .设训练样本集为第i个样本的输入,y i∈R 是对应于第i个样本的期望输出,l为训练样本数, 则LS-SVM回归问题可归结为如下优化问题:

式中:ω是权向量;e是误差向量;b是偏移项;γ是正则化参数;φ(·)是某种非线性映射.用拉格朗日法求解这个优化问题

式中, αi(i=1 ,2,…,l)是拉格朗日乘子.
定义K(xi,xj)=φ(xi)· φ(xj)是满足Mercer条件的对称函数.根据优化条件, 令L对ω, b,e, α的偏导数等于0 ,得

消去ω,e 可得以下矩阵:

通过求解线性方程组(5)求解出α,b,得到LS-SVM回归模型为

3 基于改进粒子群算法的最小二乘支持向量机
粒子群算法(particle swarm optimization ,PSO)的基本思想是通过个体之间的协作来寻找最优解[6] .在PSO 算法中, 对于每个优化问题都存在一个潜在解,可以把这些潜在解想象成d维搜索空间上的一个点, 就是通常所说的粒子.
PSO 算法的数学描述如下[7]:假设在一个d维的搜索空间中,有m个代表潜在问题解的粒子组成的一个种群, 其中表示第i个粒子在d维解空间的一个矢量点.将X 代入一个与求解问题相关的目标函数, 可以计算出其适应值.用记录第i个粒子自身搜索到的最好点(所谓最好,是指计算得到的适应值为最好, 记为pbest).而在这个种群中,至少有一个粒子是最好的, 将其编号记为g,则就是种群搜索到的最好值(记为gbest),其中g∈{1 ,2,…,m}.而每个粒子还有一个速度变量,可以用表示第i个粒子的速度.
PSO算法一般采用下式对粒子进行操作:
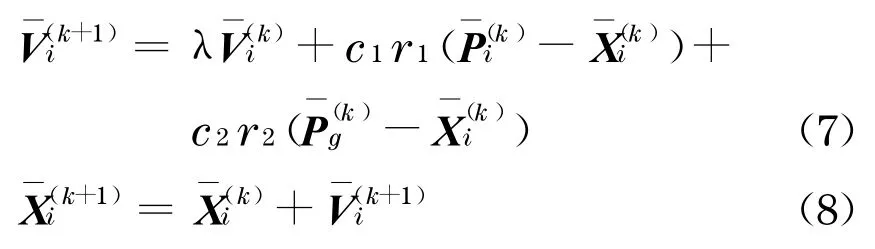
式中:粒子的标号为i=1,2,…,m;k为迭代次数;λ是惯性权重因子,它可以是一个正整数常数,也可以是以时间为变量的线性或非线性正整数, 在全局搜索和局部搜索之间, 它起到了权衡的作用;学习因子c1,c2均是正常数, 一般取值为2 ;r1,r2是均匀分布在(0,1)之间的随机数.为了控制的值在合理的区域内, 需要指定来限制.
由式(7)可知,粒子i的新速度主要通过3 部分来计算:粒子i前一时刻的速度,粒子i当前位置与它最好位置之间的距离, 粒子i当前位置与群体最好位置之间的距离.粒子i通过式(8)来更新位置坐标.通过式(7)和式(8),粒子可以决定下一步的运动位置.
PSO算法概念简单,容易实现,但是却易陷入局部极小点.针对这个问题,研究者对其做了各种各样的改进.文献[8] 指出, 在粒子的飞行过程中,粒子不仅要依靠自身经验(个体最优位置), 而且还要借鉴其余粒子的经验, 主要是借鉴那些优于该粒子本身的其余粒子的经验.因此,粒子根据下面的公式更新它的速度:

式中:c3同c1,c2为正常数;r3是均匀分布在(0 ,1)之间的随机数是从所有个体粒子中选出的满足f()≤f()的粒子个体最优位置;f(·)为适应度函数.
在PSO算法的后期, 粒子迭代速度容易变慢, 导致算法容易陷入局部最优.针对这个问题, 文献[9]提出进化速度因子H,在迭代过程中,通过计算粒子进化速度来调整粒子速度更新公式.定义进化速度因子H=,即H为上一次迭代的全局最优值与当前迭代的全局最优值的比值, 其中f(·)为适应度函数,且H≥1 .H越大,表明进化速度越快.随着迭代次数的增加, 若H值保持为1 而尚未找到最优解, 则说明PSO 算法停滞或陷入局部最优.大量实验表明,当H<Δ(如2~5)时粒子就有陷入局部最优的可能, 此时应设法改变粒子在搜索空间的位置, 帮助粒子逃离局部最优区域,继续搜索以提高粒子群的全局寻优能力.
本文改进的PSO 算法是以文献[8-9] 为基础的, 在每次迭代过程中计算粒子的进化速度, 当H≥Δ时,粒子按式(9)更新速度;当H<Δ时,则在粒子更新速度公式中加入负扰动项来改变粒子运动方向, 此时按下式更新速度:
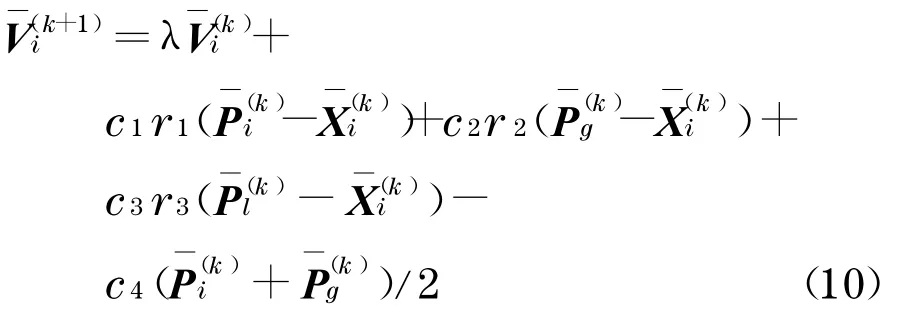
式中:c4为扰动因子, 可在0 .30~0 .65 之间取值.惯性权重λ采用线性递减策略

式中:Riter为当代迭代次数;Rmaxiter为最大迭代次数;通常λmax取0 .9 ;λmin取0 .1 .
对于LS-SV M而言,确定核函数和相关参数是非常关键的步骤.不同的核函数和相关参数使得回归LS-SVM具有不同的泛化性能.
本文采用径向基核函数形式的LS-SVM用于回归建模,需要调整2 个重要参数:正则化参数γ和核函数参数σ2.γ也称为惩罚系数,用来控制回归函数的拟合误差, γ值越大, 拟合误差越小,相应的训练时间也就越长,但是γ过大会导致过拟合;σ2是核函数参数,表示径向基核函数的带宽, 拟合误差会随着σ2的变小而变小,相应的训练时间也就变长,但是σ2过小会导致过拟合.所以参数必须精心地选择.
本文将改进的PSO算法用于LS-SVM参数优化.针对径向基核函数(radial basis function ,RBF)的LS-SV M模型参数选取可以描述为如下优化问题:

定义适应度函数如下:
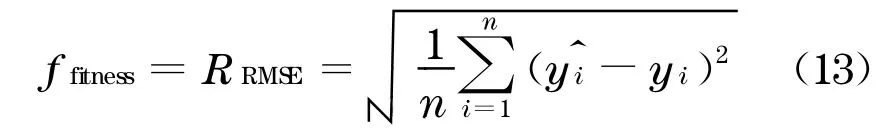
基于改进PSO的LS-SVM模型参数(γ, σ2)优化实现步骤如下:
步骤1 初始化种群规模m,最大迭代次数Rmaxiter ,以及所有粒子(γ, σ2)的初始位置X 和速度V;
步骤2 对于当前粒子(γ, σ2),用训练样本训练LS-SVM, 通过测试样本计算性能指标RRMSE;
步骤3 以RRMSE当作适应度值, 通过适应度值更新个体最优pbest和全局最优gbest;
步骤4 根据式(9)或(10)以及式(8)更新粒子(γ, σ2)的新速度和新位置;
步骤5 检查结束条件,若满足,结束寻优,返回当前最优个体为结果,否则转至步骤2 .设定结束条件为寻优达到最大迭代次数Rmaxiter或适应值小于给定精度;
步骤6 结束.
基于改进PSO 的LS-SVM软测量建模具体实现步骤如下:
步骤1 对原始样本数据进行预处理(数据变换和误差处理),随机选定l组学习样本数据及l′组测试样本数据;
步骤2 用改进的PSO 算法选取LS-SVM最优模型参数(γ, σ2);
步骤3 用最优模型参数(γ, σ2)建立LS-SV M软测量模型;
步骤4 用测试样本检验基于改进PSO 的LS-SVM软测量模型;
步骤5 结束.
4 基于IPSO-LS-SVM的作物叶水势软测量建模
本文依据SPAC 水分传输机理模型,将作物叶水势作为农田水势软测量建模研究的主要内容,建立基于IPSO-LS-SVM的作物叶水势软测量模型.
实验以大田栽培的夏玉米为检测对象.在作物周围安置传感器以获取相应的微环境信息, 采用SKPM1400 便携式数显植物压力室来测量作物叶水势, 将获取的叶水势信息作为作物叶水势软测量模型的标准值.
作物叶水势信息不仅与作物本身的蒸腾和光合作用有关,还与大气水势和土壤水势有直接的关系,所以可以将大气水势和土壤水势估计值作为作物叶水势软测量模型的2 个输入变量, 与叶层温度、叶层相对湿度、光辐射、冠层湿度、叶层与大气之间CO2体积分数差以及风速这6 个反映作物叶面蒸腾速率和光速率的辅助变量一起估算作物叶水势.但是在实际中, 大气水势和土壤水势也不能直接测量得到,所以可将影响大气水势和土壤水势的大气温度、大气湿度、土壤温度、土壤含水量、地表温度和地表湿度, 与反映作物页面蒸腾速率和光速率的6 个因素一起,作为辅助变量, 建立12 输入、1 输出的作物叶水势软测量模型.
5 仿真研究
本文数据由天津工程师范学院提供.实验数据采集人员共采集了15 d(从2009 年7 月14 日到7月23 日,7 月26 到7 月31 日), 每天从5 :30 到19 :30 每隔1 h 采集1 次.根据下式对采集的数据进行量纲一化处理,将数据标准化到[0 ,1] 之间:

式中:X min和X max分别为辅助变量X 的上下限值, 辅助变量X 经标准化处理后记为X^.
本文采用天津工程师范学院提供的125 组数据作为建模实验的样本数据.随机选取85 组数据作为训练样本,剩余的40 组数据作为测试样本.对输入数据按式(14)进行量纲一化处理, 分别建立基于标准LS-SVM,PSO-LS-SVM和IPSO-LS-SVM的作物叶水势软测量模型.
3 种模型的核函数都选择径向基核函数, 设置LS-SVM的正规化参数γ=45 .76,核参数σ2=5 .27 ;PSO和IPSO的最大迭代次数设为100,群体规模为20 .基于IPS0-LS-SVM的作物叶水势软测量结果如图3 所示.3 种模型的误差结果如表1 所示.

图3 基于IPSO-LS-SV M的软测量实验仿真图Fig .3 Simu lations of modeling on IPSO-LS-SVM

表1 LS-SVM, PSO-L S-SVM, IPSO-LS-SV M误差结果比较Tab.1 Comparison of error results of LS-SV M,PSO-LS-SVM, IPSO-LS-SV M
由表1 可知,采用IPSO-LS-SVM建立的作物叶水势软测量模型精度比采用标准LS-SVM建立的模型精度高, 预测效果好;与采用PSO-LS-SVM建立的模型相比,精度相差不多,但是模型训练时间少.此外,采用该方法预测作物叶水势比采用统计回归[10]和定量遥感[11]方法预测作物叶水势的估计精度高.
6 结论
PSO 是一种群智能优化算法, 具有算法实现简单,运算速度快等多方面的优点.本文把LS-SVM模型参数的选取当作优化问题,利用PSO 算法来快速寻找到最优LS-SVM模型参数, 并在基本PSO算法的基础上改进了粒子速度更新公式, 提出了基于改进PSO 算法(IPSO)的LS-SV M, 将它用来作为预测作物叶水势的一种方法, 建立了基于IPSO-LS-SVM的作物叶水势软测量模型.仿真结果表明, 基于IPSO-LS-SVM的模型能够很好地预测作物叶水势.
[1] 康绍忠,刘晓明, 熊运章.土壤植物大气连续体水分传输理论及其应用[M] .北京:中国水利水电出版社, 1992:15-17.KANG Shaozhong,LIU Xiaoming,XIONG Yunzhang .Water transfer theory and the application in soil plant atmosphere continuum[M] .Beijing :China Water Power Press, 1992:15-17.
[2] 卢胜利, 田立国, 孙文君, 等.面向精准灌溉的农田水势软测量[J] .天津工程师范学院学报, 2007, 17(4):1.LU Shengli, TIAN Liguo,SUN Wenjun et al.Soft-sensing of farm land water poten tial for precision ir rigation[J] .Jou rnal of Tianjin University Technology and Education, 2007, 17(4):1.
[3] Philip J R.Plan t w ater relations:some physical aspects[J] .Annual Review of Plan t Physiology,1966, 17(1):245.
[4] 信秀丽, 徐富安, 张佳宝, 等.一种适用于土壤水势定位观测的新仪器[J] .土壤, 2005, 37(3):326.XIN Xiuli, XU Fuan, ZHANG Jiabao, et al.A new instrument for monitoring soil moisture in field[J] .Soils, 2005,37(3):326.
[5] Suykens J A K,Vandew alle J.Least squares support vector machine classifiers[J] .Neural P rocessing Letters, 1999, 9(3):293.
[6] EL-Naggar K M, AIRashidi MK,AI-Othman A K.Estimating the input-output parameters of thermal power plants using PSO[J] .Energy Conversion and Management, 2009, 50(7):1767.
[7] Yu J B,Wang S J, Xi L F.Evolving artificial neu ral networks using an improved PSO and DPSO[J] .Neu rocomputing,2008,71(4-6):1054.
[8] 王志刚.一种改进的粒子群算法[J] .哈尔滨商业大学学报:自然科学版, 2009, 25(4):464.WANG Zhigang .Amodified particle sw arm optim ization[J] .Journal of Harbin University of Commerce:Natu re Sciences Edition, 2009, 25(4):464.
[9] 陈如清, 俞金寿.基于粒子群最小二乘支持向量机的软测量建模[J] .系统仿真学报, 2007, 19(22):5307.CH EN Ruqing,YU Jinshou.Soft sensor modeling based on partic le sw arm optim ization and least square vector machines[J] .Jou rnal of Sy stem Simu lation, 2007, 19(22):5307.
[10] 康绍忠,熊运章, 王振益.土壤—植物—大气连续体水分运移的力能关系的田间试验研究[J] .水利学报, 1990, 6(7):1.KANG Shaozhong,XIONG Yunzhang,WANG Zhenyi.Distribution of hy draulic resistance and water potential in soilplant-atmosphere continuum [J] .Journal of H ydrau lic Engineering,1990, 6(7):1.
[11] 张杰, 张强, 赵宏, 等.定量遥感反演作物水势的原理及其应用[J] .生态学杂志, 2008, 27(6):916.ZH ANG Jie, ZH ANG Qiang,ZH AO H ong .Theory and application of leaf w ater potential retrieved from remote sensing[J] .Chinese Journal of Ecology,2008, 27(6):916.
