基于经济资本管理系统的商业银行贷款决策方法研究*
2010-12-19彭建刚梁国栋张丽寒黄向阳
彭建刚,梁国栋,张丽寒,黄向阳
(湖南大学金融学院,湖南长沙 410079)
基于经济资本管理系统的商业银行贷款决策方法研究*
彭建刚,梁国栋,张丽寒,黄向阳
(湖南大学金融学院,湖南长沙 410079)
基于巴塞尔新资本协议和CreditRisk+模型,以数据仓库为基础设计了商业银行经济资本管理系统,这一系统包括以EVA为目标函数、以经济资本限额等为约束条件构建的商业银行贷款决策最优化模型。通过该系统可以实现任一贷款组合的经济资本计量,该系统可有效地运用于经济资本约束条件下商业银行的贷款优化决策。
商业银行;经济资本;贷款决策;数据仓库
一 引 言
将经济资本管理与贷款决策有机地结合起来是我国商业银行需要解决的现实问题,美国金融危机的爆发更加凸现了其紧迫性。商业银行需要建立一经济资本管理系统,通过这一系统可将违约概率的测定、违约损失率的测定、经济资本的在线实时计量、经济资本限额分配、贷款的最优决策组成一完整的操作链条。
本文基于巴塞尔新资本协议和CreditRisk+模型,以数据仓库为基础,设计了商业银行经济资本管理系统。该系统以EVA(经济增加值)最大化为目标,以经济资本限额和经济资本回报率为约束条件,通过建立贷款决策的最优化模型对备选贷款项目进行选择。
二 商业银行经济资本管理系统的核心内容
(一)商业银行经济资本的计量
本文使用CreditRisk+模型计量贷款组合所应占用的经济资本。根据本课题组提出的加权平均频带划分方法,[1]商业银行计量经济资本的过程如下:
贷款组合的违约损失分布的概率生成函数可以表示为各个组合子集违约损失分布概率生成函数的乘积,[2]即:
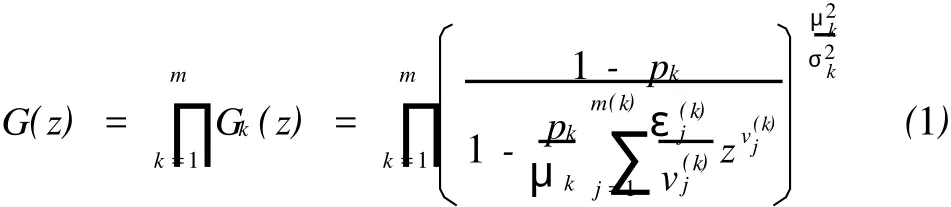
其中:μk——组合第k个子集违约事件个数的均值;
σk——组合第k个子集各笔贷款违约率的标准差之和;
——组合第k个子集中敞口区间j的预期损失;
——组合第k个子集中敞口区间j的共同敞口。
计算损失分布的递推式如下:

因此整个贷款组合所应占用的经济资本为:

(二)贷款决策最优化模型的构建
式(6)可以计量任一贷款组合应占用的经济资本。当商业银行新增X笔贷款,采用式(6)计量新的贷款组合应占用的经济资本,其中X笔新增贷款的风险贡献等于新贷款组合的经济资本与原贷款组合的经济资本之差。作贷款决策时,我们不仅要考虑经济资本限额对风险的锁定,还要考虑在一定风险水平上的银行效益最大。基于这一思想,本文提出的贷款决策最优化模型将 EVA作为目标函数,以经济资本限额、RAROC等为约束条件,运用数学规划方法确定各备选贷款项目的优化方案。如,假设现有M笔备选贷款项目,根据贷款决策最优化模型可以确定贷款发放的最优选择方案。
1.贷款决策的最优化目标
本文将EVA作为贷款决策的最优化目标,用公式表示如下:
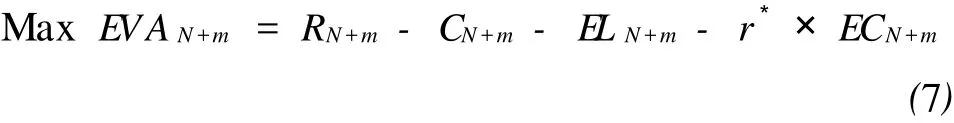
其中:EVA——经济价值增加值;
R——贷款组合的收益;
C——成本(包括资金成本和营运成本);
EL——贷款组合的预期损失;
r*——经济资本最低回报率,;
EC——贷款组合所占用的经济资本;
m——将要发放的贷款笔数。
在原有贷款的基础上新增m笔贷款,是在充分考虑备选贷款与原有贷款以及备选贷款之间的风险分散效应后进行的贷款决策,即追求新的贷款组合EVA值最大。
2.贷款决策的主要约束条件
1)经济资本限额的约束。本文假定某商业银行的经济资本限额已经确定。其分支行所占用的经济资本总量不能超过此限额,否则经济资本就无法覆盖贷款所产生的非预期损失。因此,该商业银行在经营活动中所占用的经济资本额一定要控制在经济资本的限额范围内。
设某分支行可配置的经济资本限额为EC*,该分支行已发放N笔贷款,这一贷款组合占用的经济资本为ECN、预期损失为EL N。在N笔贷款的基础上又新增m笔贷款后,新贷款组合占用的经济资本为ECN+m、预期损失为EL N+m,则经济资本限额的约束条件为:

式(8)是贷款决策最优化模型的第一个约束条件。
2)经济资本最低回报率的约束。商业银行根据其战略目标设定一个最低回报率。商业银行在经营过程中的RAROC值不得低于这个最低回报率。
设某商业银行确定的经济资本最低回报率为r*,则经济资本最低回报率的约束条件为:

式(9)是贷款决策最优化模型的第二个约束条件。
3.贷款决策最优化模型
根据贷款决策最优化的目标方程(7)以及约束条件式(8)、式(9),贷款决策的最优化模型可表示为:

其中:RAROC——风险调整资本回报率;
Ri——第i笔贷款的收益;
Ci——第i笔贷款的成本;
N——已发放的贷款笔数;
M——备选贷款笔数;
m——将要发放的贷款笔数。
在多笔备选贷款项目中,商业银行根据贷款决策最优化模型(10),可得出不同笔数下贷款决策的优化方案。
(三)运用数据仓库实现经济资本管理和贷款项目的最优选择
1.数据仓库的整体架构设计
在本文中,数据仓库用于商业银行经济资本的计量和新增贷款项目的最优决策。[3]其整体架构围绕这两个主题设计,分三个模块。
第一个模块是基本数据采集与存储模块。该模块对商业银行贷款的原始数据进行整理,并将整理后的数据按一定的标准分类存储。
第二个模块是经济资本计量与决策分析模块。该模块的主要过程为:首先依据存储模块中整理后的数据计算出每笔贷款的违约损失率和违约概率,利用CreditRisk+模型计量贷款组合的预期损失和非预期损失;然后依次将各笔备选贷款项目加入到原贷款组合中,形成新贷款组合,再利用CreditRisk +模型计量新贷款组合的预期损失和非预期损失,并求出其对应的风险贡献;最后运用贷款决策最优化模型确定备选贷款项目的优先次序。
第三个模块是数据访问模块。该模块存入第二模块的分析结果,并可通过应用程序对该模块进行访问,便于商业银行管理层做出最优决策。
2.基于数据仓库的商业银行经济资本管理的流程
1)贷款原始数据的处理。我们将商业银行的贷款原始数据进行以下处理:首先,消除数据噪声。在原始数据采集和录入过程中,存在一些人为失误或数据传输过程中的误差,在计量贷款组合经济资本前需消除这些误差。其次,解决数据不一致问题。贷款原始数据可能源于商业银行的多个业务部门,这些部门数据存储方式和数据结构缺乏统一标准,在计算前需把这些数据作规范化处理使其具有一致性。最后,删除冗余数据。由于上述业务部门相关人员考虑不周或其他原因可能产生重复的数据字段,使用前需将其删除。
2)违约概率和违约损失率的确定。违约概率作为计量信用风险的关键参数之一,其测算的准确性决定了商业银行信用风险管理的水平。本文使用了本课题组于2008年提出的贷款违约表法[4,5]测算借款人的违约概率。由于我国商业银行数据库中目前的数据还不足以对债务人的违约损失率进行精确的测算,故依据巴塞尔新资本协议关于内部评级法中初级法的规定,违约损失率取新资本协议提供的参照值。
3)贷款组合的频带划分。采用加权平均法给贷款组合划分频带,操作过程如下:首先,“客户端软件”读取银行管理者输入的频带个数和调整参数①调整参数的取值范围在0—0.5之间.,将这两个参数传输给数据仓库。其次,从基本数据存储模块中取出贷款组合的相关数据,将各贷款按其风险敞口的大小升序排列,将组合内所有贷款项目按笔数均匀分组,将每组内贷款的暴露加权平均,若平均值与其最接近整数的差值的绝对值大于银行管理者输入的调整参数,则将该组内的贷款笔数进行微调,直至差值的绝对值小于或等于该参数,将上述整数作为该频带的公共敞口。然后,确定各频带的序号、贷款笔数和公共敞口,计算各频带的预期违约个数和预期损失(频带的公共敞口与其对应的预期违约个数的乘积),将这些数据存入数据仓库。
4)经济资本的计量。取以上数据并采用CreditRisk+模型计量置信度为99.9%时的VaR值。将各个频带的预期损失相加得到贷款组合的预期损失。将该VaR值与组合的预期损失相减求得贷款组合的非预期损失,数值上等于组合应占用的经济资本。
5)贷款决策最优化的实现。经济资本管理系统把M笔备选贷款的2M-1种组合依次加入到原贷款组合,组成新的贷款组合,分别计量新贷款组合所占用的经济资本、EVA值和RAROC值。在新贷款组合经济资本占用额不超过经济资本限额、RAROC不小于经济资本最低回报率的条件下,贷款决策最优化模型确定不同贷款笔数对应的最优贷款方案。
6)经济资本管理系统示意图。
综上所述,现将商业银行经济资本管理系统如图1。
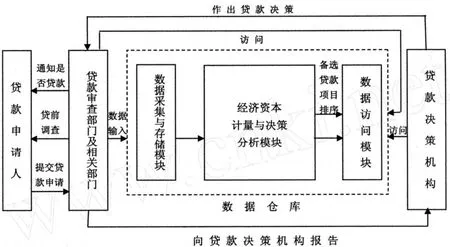
图1 商业银行经济资本管理系统示意图
(四)算例分析
本节通过算例分析说明这一经济资本管理系统的有效性。本算例分析使用了我国某城市商业银行2007年的数据。为便于分析,只选取了该行建筑业和制造业两个部门的部分贷款数据。
1.样本数据的选取
选取该城市商业银行于2007年1月发放的300笔1年期公司贷款作为样本数据,其中建筑业70笔,制造业230笔,具体情况见表1。

表1 样本贷款数据 单位:笔
2.原贷款组合所占用经济资本的计量
根据贷款违约表法计算出2005年、2006年和2007年三年的一年期公司贷款的违约概率。结果如表2所示。
根据式(2),式(3)和式(4)参照加权平均的频带划分方法,结合表4计算出预期损失和非预期损失。为消除因频带个数的不同而引起计算结果的微小波动,本文随机抽取了10种不同的频带划分方式,分别计算并取其平均值,测算出的预期损失和非预期损失分别为615.83万元和3劳成疾001.16万元。贷款组合应占用的经济资本在数值上等于其非预期损失。故原贷款组合的经济资本占用额为3 001.16万元。图2是该贷款组合的违约损失分布图(其中一种频带划分方式)。

表2 2005年~2007年一年期公司贷款的违约概率
根据表2计算出各信用等级债务人违约率的均值和标准差,结果如表3所示。

表3 各信用等级债务人违约率的均值和标准差
根据表3可计算出CreditRisk+模型所需的各种参数值,结果见表4。

表4 模型的计算参数

图2 贷款组合的违约损失分布图(单位:20万元)
3.备选贷款项目的最优选择
我们对模型的参数作出如下设定:
1)该城市商业银行现有7笔备选贷款项目,每一备选贷款项目分别标号1~7;
2)该行原发放300笔贷款的成本(含资金成本和经营成本)为1000万元;
3)增加一笔贷款时成本会发生变化,在本算例分析中,假设组合的经营成本保持不变,但资金成本相应增加;
4)该行的经济资本限额EC*为3020万元;
5)最低经济资本回报率r*为10%。
根据式(10),该城市商业银行的贷款决策最优化模型可以表示为:


将7笔备选贷款分别加到原贷款组合中,共形成127个新贷款组合,分别计算其经济资本占用额和EVA值。我们选取限额内不同贷款发放笔数下EVA值最大的贷款组合,结果如表5所示。

表5 贷款决策最优化模型算例分析结果
由表5可知:
1)如果只考虑新增1笔贷款,标号为4的备选项目为最优。但商业银行往往在经济资本限额内,会决定同时发放多笔贷款,故应根据贷款发放的笔数考虑最优方案。
2)在经济资本限额内,对应每一新增贷款发放笔数,存在一种EVA值最大的最优选择。例如,新增2笔贷款时,发放标号为1和标号为4的两笔贷款为最优,原有的贷款组合加上这两笔贷款其EVA值为129.75万元,别的选择都会低于该值。
3)新增贷款笔数较多的新贷款组合其经济资本占用可能小于新增贷款笔数较少的新贷款组合。本例中,新发放4笔贷款比新发放3笔贷款,总的经济资本占用额较小。表明存在贷款组合的风险分散效应。
4)新发放贷款6笔以上,经济资本占用都将超限额,故备选方案中不予考虑。
5)拟发放贷款组合{1,3,4,5}对应的新贷款组合在约束条件之内,其对应的EVA值141.54万元在所有满足约束条件的贷款发放方案中最高。因此,该贷款方案是本算例中银行的最优选择。
6)表5提供了在经济资本限额内,对7笔备选贷款项目的各种发放方案,该城市商业银行可根据实际情况作最后的决策。
(五)结论
这一经济资本管理系统,商业银行可在经济资本约束条件下实现贷款决策优化,实现贷款组合一定风险水平下的效益最大。
[1] 彭建刚,张丽寒,刘波,屠海波.聚合信用风险模型在我国商业银行应用的方法论探讨[J].金融研究,2008,(08):72-85.
[2] Credit Suisse Financial Products,1997.CreditRisk+:A credit risk management framework[OL].http://www.csfb.com/ creditrisk.
[3] 朱云,邱菀华.基于数据仓库的银行信用评级模型的构建[J].企业经济,2006,(10):137-139.
[4] 彭建刚,屠海波,何婧,周颖辉.有序多分类logistic模型在违约概率测算中的应用[J].财经理论与实践,2009,(4):2-7.
[5] 彭建刚,易宇,李樟飞.测算商业银行贷款违约概率的贷款违约表法探讨①注:该文曾在2009年中国金融工程学年会上宣读.[J].管理学报,2009,(06):828-833.
Research on the Loan-decision Method based on Economic Capital Management System of Commercial Banks
(College of Finance,Hunan University,Changsha 410079,China)
PENG Jian-gang,LIANG Guo-dong,ZHANG Li-han,HUANG Xiang-yang
Based on the New Basel Capital Accord and Credit Risk+model,we designed an economic capital management system for commercial banks.By using of the system,we can realize online real-time measurement of economic capital of any loan portfolio.The system also constructs the optimal commercial bank loan-decision model,which has the EVA as objective function and economic capital limitation as constraint.The system can be used to make loan-decision for commercial banks effectively on the constraint of economic capital.
commercial bank;economic capital;loan-decision;data warehouse
F832
A
1008—1763(2010)02—0042—06
2009-11-08
国家自然科学基金项目(70673021);教育部科学技术研究重大项目(309023);教育部博士点基金项目(20060532011);湖南省研究生科研创新项目(CX2009B062)
彭建刚(1955—),男,湖南长沙人,经济学博士,湖南大学金融学院教授、博士生导师.研究方向:金融管理与金融工程.
