一类广义 Schrödinger方程的双 W ronskian解＊

吴妙仙

(浙江广厦建设职业技术学院信控分院,浙江东阳 322100)

0 引 言

非线性发展方程的精确求解问题已形成了许多重要的方法,如反散射方法[1]、Darboux变换方法[2]、Hirota方法[3]、Bäcklund变换[4]及 W ronskian技巧[5-6]等.其中 ,W ronskian技巧有着鲜明的特点 ,这不仅因为W ronskian行列式本身所具有的特性使得由W ronskian行列式形式构成的解可以直接代入到方程中进行检验,而且通过这种解的表示还可以求得除孤子解以外的其他形式的精确解,如有理解、positon解、negaton解、complexiton解、breathers解等[7-9].

目前,W ronskian技巧已经有效地应用到许多经典的可积系统中,如 KdV方程、MKdV方程、KP方程、Boussinesq方程、非线性 Schrödinger(NLS)方程及带导数项的非线性 Schrödinger方程等.最近,一些学者已成功地将该技巧应用于若干等谱与非等谱方程及变系数方程中.例如:文献[10]研究了等谱二阶 AKNS方程的双W ronskian解;文献[11]研究了非等谱 KP方程的双 W ronskian解;文献 [12]研究了一类变系数 NLS方程的双W ronskian解.

本文研究一类在珀色-爱因斯坦凝聚态中有着重要应用的一类广义非线性 Schrödinger方程

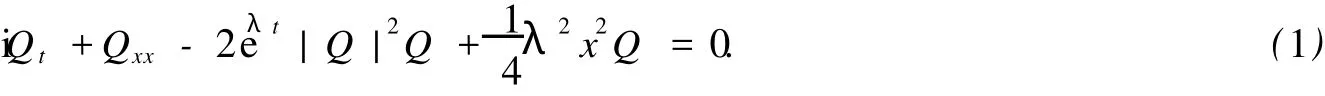
式(1)中:λ为实参数;Q(t,x)为宏观波函数;t,x分别为时空变量.方程 (1)从形式上看是经典Schrödinger方程的变系数推广,其孤子解和周期解结果见文献[13].方程 (1)的 Lax对可表示为

式 (2)中:φ为波函数;

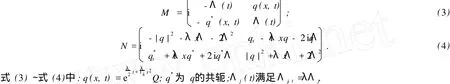
1 W ronskian解

若在方程 (1)中施以分式变换

F,G均为 x,t的复函数,则 F与 G满足下列方程:

其中 D是著名的 Hirota双线性导数算子,定义为

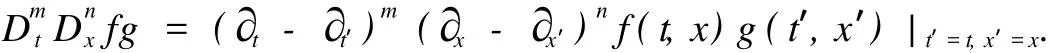
考察矩阵方程组

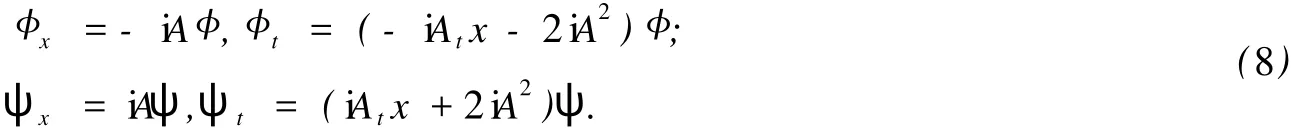
式 (8)中:φ,ψ为列向量,φ =(φ1,φ2,…,φ2N)T,ψ=(ψ1,ψ2,…,ψ2N)T;A是关于 x与 t的 2N ×2N 阶矩阵函数,且满足

令 PN×M,QN×M为如下 N ×M阶矩阵:

因此,方程 (6)和方程 (7)可转化为双线性方程组

为了证明的需要,先给出以下几个引理:

引理 1[15]设 D是 N ×(N-2)阶矩阵,a,b,c,d是 N维列向量,则

引理 2[5]设αj(j=1,2,…,n)是具有 n个分量的列向量,而γj(j=1,2,…,n)是不为零的 n个任意常数,则

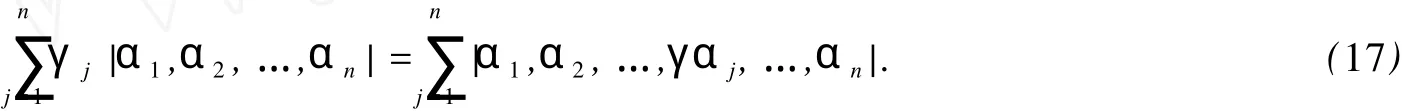
式 (17)中 γ αj是列向量 ,即

引理 3[16]设 P=(pij)是 n×n阶算子矩阵,其元素 pij是微分算子,B=(bij)是 n×n阶函数矩阵,以表示矩阵 B的列向量与行向量,则

注 1 式 (19)说明算子 pij分别作用于各列向量相应元素所得 n个行列式之和与 pij分别作用于行列式各行向量相应元素所得 n个行列式之和相等.

引理 4 设 A是与 x无关的 2N×2N阶矩阵函数,且满足式 (9),则在条件 (8)下,类似于文献 [14]中的推导,有:

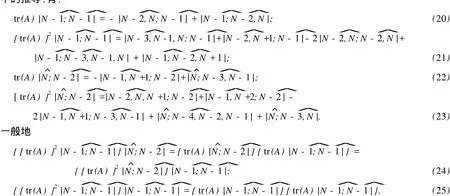
定理 1 若 A是与 x无关的 2N ×2N阶矩阵,且满足 At=λA,则方程 (14)和方程 (15)在条件 (8)下有双W ronskian行列式解:

证明 先证双 W ronskian行列式 (26)满足式 (14).记Δ=2ie-λt,则易得 F,G对 x的导数分别为:

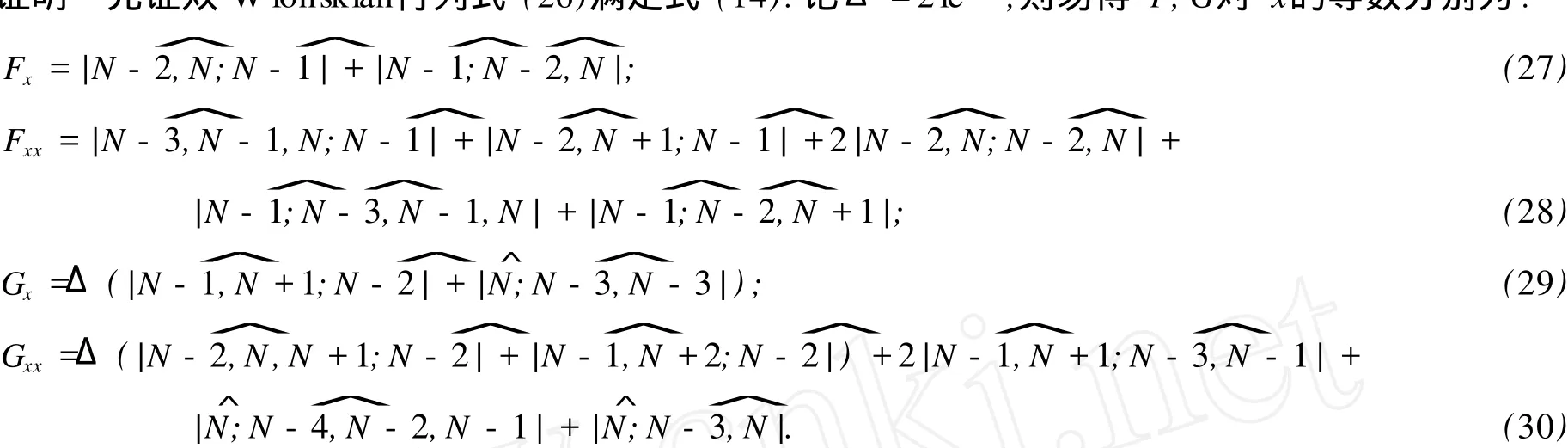
其次,在条件 (8)下又可算得:

将式 (27)～式 (32)代入到方程 (14)的左端,得

注意到式 (24),方程 (14)的左端可化为

利用引理 1,不难推知:

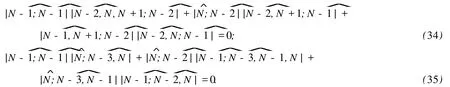
因此,式 (33)恒为零,从而式 (14)成立.同样地可证得式 (26)亦满足式 (15).定理 1证毕.

因此,方程 (1)的解可表示为

2 类有理解

一般地,矩阵方程组 (8)的通解可表示为

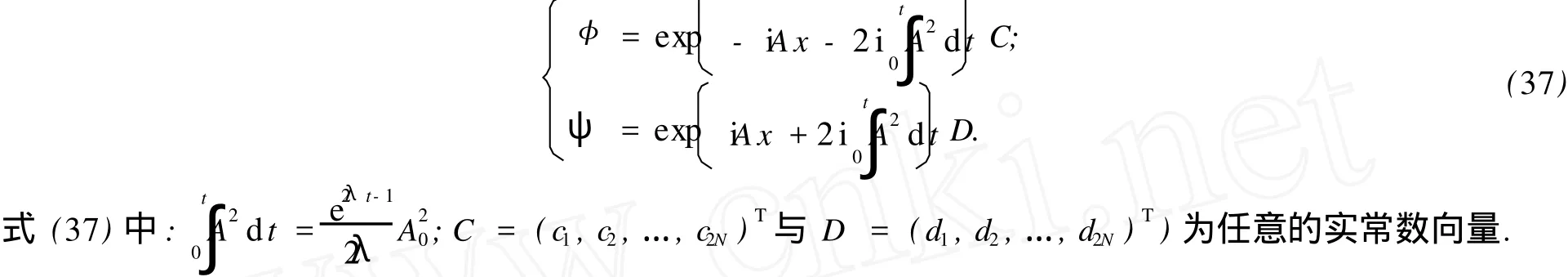
求解矩阵方程 (9)得 A=eλtA0(A0为任意常数矩阵),将其代入到式 (37)并展开为级数形式,得

断为有限项

此时,相应的分量可写为:

因此,可求得方程W ronskian形式的类有理解,其对应的前 3个类有理解分别为:

当然,上述关于类有理解的结果亦可直接代入方程进行检验.

3 结 语

对于广义非线性 Schrödinger方程 (1),在 Lax对基础上给出构成解的双W ronskian行列式的列向量φ与ψ所满足的矩阵方程,并结合 Hirota方法与W ronskian技巧讨论了方程 (1)的双W ronskian形式的解.在矩阵函数 A要求满足 Al=λA的条件下,取 A=eλlA0(这里 A0为任意常数矩阵),求得含任意常数矩阵 A0的 φ与ψ的通解,并将其展开为 A0的幂级数.于是,当 A0取相应的特殊矩阵时即可算得方程(1)的类有理解.本文给出的求双W ronskian解方法还可以应用到其他的可积方程中.此外,对于方程(1),当 A0取其他特殊矩阵时,还可以求得如 positon解、negaton解、complexiton解等其他形式的精确解,关于此方面的结果将另文给出.

[1]AblowitzM J,Clarkson P A.Solitons,nonlinear evolution equations and inverse scattering[M].Cambridge:Cambridge University Press,1991.

[2]谷超豪,胡和生,周子翔.孤子理论中的达布变换及其几何应用[M].上海:上海科学技术出版社,1999:53-58.

[3]Hirota R.Exact solution to the KdV equation formultiple collisions of solitons[J].Phys RevLett,1971,27:1192-1194.

[4]Hu X B.A Bäcklund transformation and nonlinear superposition formula of a modified KdV-type bilinear equation[J].J Math Phys,1994,35:4379-4745.

[5]FreemanN C,Nimmo J J C.Soliton solutionsof the Korteweg deVries and Kadomtsev-Petviashvili equations:theW ronskian technique[J].Phys LettA,1983,95(1):1-3.

[6]MatveevV B.GeneralizedW ronskian formula for solutions of the KdV equation[J].PhysLettA,1992,166(3/4):205-208.

[7]Yao Yuqing,Ji Jie,Liu Yuqin,et al.Soliton solutions,rational solutions,Matveev solutions,complexions and mixed solutions for three(2+1)-dimension equations[J].PhysLettA,2008,372(6):786-797.

[8]Li Chunxia,MaWenxiu,Liu Xiaojun,et al.W ronskian solutions of the Boussinesq equation:solitons,negatons,positons and complexitons[J].Inverse Problems,2007,23(1):279-296.

[9]张翼,颜姣姣,褚俪瑾.KdV方程矩阵形式的精确解[J].浙江师范大学学报:自然科学版,2009,32(2):126-132.

[10]Sun Yunpen,Bi Jinbo,Chen Dengyuan.N-soliton solutions and doubleW ronskian solution of the non-isospectralAKNS equation[J].Chaos,Solitons and Fractals,2005,26(3):905-912.

[11]Ji Jie.The doubleW ronskian solutions of a non isospectral Kadomtsev-petviashvili equation[J].PhysLettA,2008,372(39):6074-6081.

[12]LüXin,Zhu Hongwei,Yao Zhenzhi,et al.Multisoliton solutions in ter msof doubleW ronskian deter minant for a generalized variable-coefficient nonlinear Schrödinger equation from plas ma physics,arterial mechanics,fluid dynamics and optical communications[J].Annals of Physics,2008,323(8):1947-1955.

[13]Zhang Yi,Xu Hongxian,Yao Caizeng,et al.A classof exact solutionsof the generalized nonlinear Schrödinger equation[J].ReportsonMathematical Physics,2009,63(3):427-439.

[14]Nimmo J J C.A bilinearBäcklund transfor mation for the nonlinear Schrödinger equation[J].PhysLettA,1983,99(6/7):279-280.

[15]陈登远.孤子引论[M].北京:科学出版社,2006.

[16]陈登远,张大军,毕金钵.AKNS方程的新双W ronskian解[J].中国科学:A辑 数学,2007,37(11):1335-1348.