第一性原理计算Fcc-Cr1-x Si x N的调幅分解

高巍,谢飞

(河北大学质量技术监督学院,河北保定 071000)

第一性原理计算Fcc-Cr1-xSixN的调幅分解

高巍,谢飞

(河北大学质量技术监督学院,河北保定 071000)

基于通过第一性原理计算方法,计算了三元固溶体Fcc-Cr1-xSixN总能,在此基础上计算了其分离能和调幅分解线.结果说明,Fcc-Cr1-xSixN是亚稳相,能够经调幅分解机制分解为Fcc-CrN和Fcc-SiN.组元相形成的应变能小于分离能,不会抑制Fcc-Cr1-xSixN的调幅分解.Fcc-Cr1-xSixN的Si含量为渗透阈值时,不会发生调幅分解.Fcc-Cr1-xSixN可能经调幅分解生成Fcc-SiN.

超硬薄膜;调幅分解;第一性原理

近年来纳米复合超硬薄膜材料得到了广泛研究,特别是在TiN薄膜上加入Si元素后形成的Ti-Si-N薄膜倍受关注[1-3].目前,开发新型材料仍然是此类超硬材料的研究重点内容之一.Cr-Si-N薄膜作为一种很有希望的纳米复合超硬薄膜候选材料,得到了很多关注.近来已有研究者用不同方法制备了Cr-Si-N薄膜,并且获得了满意的硬度[4-5].

在已经得到研究的Ti-Si-N和Ti-B-N纳米复合超硬薄膜系统中,固溶体相均具备调幅分解机制[6-8],从而保证了薄膜制备过程中TiN相和SiNy相(或BN相)自动分离,形成明锐界面,这对于此类纳米复合超硬薄膜系统获得超硬度起着重要作用[6-9].所以,Fcc-Cr1-xSixN固溶体是否具备调幅分解机制令研究者感兴趣.但是,由于实验困难,Cr-Si-N系统的相图不够完备,目前仍缺乏关于Cr-Si-N系统的调幅分解机制的认识.另一方面,第一性原理计算作为有效的计算实验手段,已经对Ti-A l-N[10-12],Cr-A l-N[13-14],Cr-A l-N[15],Ti-Si-N[6-7],Ti-B-N[8]薄膜系统的调幅分解特性作出了预测和比较.所以应用第一性原理计算方法对Fcc-Cr1-xSixN固溶体的调幅分解机制进行预测是合理的.

本文基于热力学计算模型,使用第一性原理平面波赝势计算方法计算了Fcc-Cr1-xSixN固溶体的调幅分解机制,得到的计算结果能为今后关于Cr-Si-N薄膜的研究打下理论基础.

1 计算模型和方法

Fcc-Cr1-xSixN由8个原子组成的晶胞周期排列形成.x=0时(Fcc-CrN)为理想立方结构CrN晶体,属于FM-3M空间群,α=β=γ=90°,晶格常数a=b=c=0.46 nm,晶胞内包含4个Cr原子和4个N原子,非对称原子分数坐标为Cr(0,0,0),N(0.5,0.5,0.5).x=0.25,0.5,0.75时可以视为CrN的8原子晶胞中分别有1,2,3个Cr原子由Si原子替代.x=1时(Fcc-SiN)可以视为CrN晶胞中全部Cr原子由Si原子替代.Fcc-Cr1-xSixN的晶体结构如图1所示.

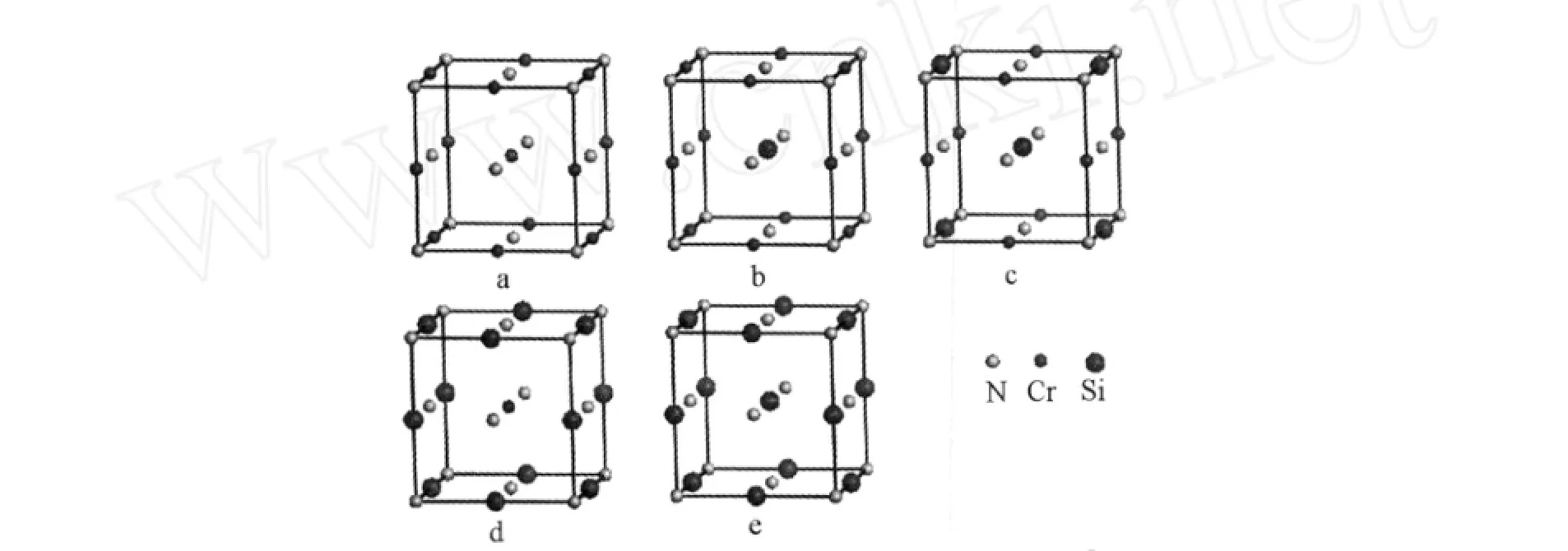
图1 Fcc-Cr1-x Si x N的晶体结构Fig.1 Crystal structures of Fcc-Cr1-x Si x N

计算时交换关联能采用广义梯度近似(GGA)下的PBE96.布里渊区的求和采用线性四面体积分法,在倒空间用四面体方法对布里渊区中的64个点积分.计算中使用的Cr,Si和N原子的原子球半径分别为2,2和1.6.

2 计算结果和讨论

2.1 分离能

分离能ΔH定义为

式中E(Fcc-Cr1-xSixN),E(Fcc-CrN),E(Fcc-SiN)分别为经第一性原理计算得到的Cr1-xSixN,Fcc-CrN, Fcc-SiN的总能量.分离能为正值,说明Fcc-Cr1-xSixN的能量大于Fcc-CrN和Fcc-SiN混合态的能量,Fcc-Cr1-xSixN具有相分解的趋势,并且分离能越大,相分解的趋势越明显;分离能为负值,表明固溶体相Fcc-Cr1-xSixN不会相分解.

图2为Fcc-Cr1-xSixN的分离能,图中分离能恒为正值,说明Fcc-Cr1-xSixN是亚稳相,具有分解为Fcc-CrN和Fcc-SiN的趋势.图2中Fcc-Cr1-xSixN的分离能曲线表现出不对称性,偏向了x较大一侧,最大值出现在x=0.66处,说明在混溶过程中,和Fcc-SiN溶入Fcc-CrN相比,Fcc-CrN溶入Fcc-SiN更为不易(即相分解趋势更明显).

2.2 调幅分解线

将Fcc-Cr1-xSixN系统视为由Fcc-CrN和Fcc-SiN组成的伪二元合金系统,其混合自由能ΔG定义为[12]

式中R为气体常数;T为热力学温度.根据热力学原理,固溶体发生调幅分解的临界条件为d2ΔG/dx2= 0[13].按照临界条件可以做出调幅分解线.Fcc-Cr1-xSixN满足的成分和温度条件位于调幅分解线包容区域内,能够发生调幅分解;位于调幅分解线外,能够保持固溶体结构或以形核-长大的方式进行相分解.

图3给出了Fcc-Cr1-xSixN的调幅分解线(图中实线).图中最高温度为2 750 K,出现在x=0.73处,说明调幅分解线也具有不对称性,这是由分离能的不对称性决定的.图中1 000 K温度(典型沉积温度)所对应的调幅分解范围是x=0.42～0.96(如箭头所示).温度低于500 K时,对应的调幅分解范围是x=0.4～0.98.这些结果说明,在较大成分和温度范围内,Fcc-Cr1-xSixN符合调幅分解的热力学条件.

纳米复合薄膜产生超硬度的一个条件是包裹纳米晶相的非晶相具有单原子层厚度[9],以细化晶粒,减小应变能或抑制裂纹缺陷.满足此条件时,Si的质量分数为6%～12%(x=0.12～0.24),称为渗透阈值[16].图3中,温度为1 000 K时,渗透阈值已经位于调幅分解线之外(如粗虚线所示),这说明Si含量为渗透阈值时, Fcc-Cr1-xSixN可能不会发生调幅分解.

2.3 应变能

弹性应变能Es定义为

式中S为分解相CrN和Fcc-SiN之间的界面面积,Y为单位界面面积上应变能,定义为[7]

式中G为CrN的弹性模量,v为泊松比,t为晶粒尺寸,ε为CrN和Fcc-SiN之间的晶格错配度.式(3)适用于晶格错配度比较小的情况,由于CrN和Fcc-SiN的晶格错配度达到了4%,所以按照式(3)计算得到的弹性应变能应该看作CrN和Fcc-SiN之间的应变能的上限值.

若分解相的弹性应变能小于分离能,调幅分解才能发生.图4给出了Fcc-Cr1-xSixN的弹性应变能和分离能的比较结果,可以看到,弹性应变能远小于分离能,不会抑制Fcc-Cr1-xSixN的调幅分解.

2.4 晶格常数

Fcc-SiN是亚稳相,倾向于转变为更稳定的β-Si3N4.在Fcc-Cr1-xSixN相分解时,如果形成β-Si3N4的相变阻力较大,Fcc-SiN可能作为共格亚稳新相出现.如果形成β-Si3N4的相变阻力较小,Fcc-SiN可能直接转变为β-Si3N4,抑制调幅分解.下面从晶格常数的角度对此做一分析.图5给出了计算得到的Fcc-Cr1-xSixN的晶格常数,其中Fcc-CrN和Fcc-SiN的晶格常数分别为0.406 nm和0.42 nm,单原子占据的晶胞体积分别为8.37×10-3nm3和9.26×10-3nm3.另外,计算得到了β-Si3N4的晶格常数a=0.754 nm,c=0.287 nm,单原子占据的晶胞体积为11.65×10-3nm3.根据以上结果,CrN和Fcc-SiN的晶胞体积差异为10.6%, CrN和β-Si3N4的晶胞体积差异为28%.可以看到,形成β-Si3N4将造成较大的晶胞体积差异,具有较大相变阻力.所以Fcc-Cr1-xSixN可能经调幅分解生成Fcc-SiN.

3 结论

使用第一性原理计算方法,计算了Fcc-Cr1-xSixN固溶体的分离能、调幅分解曲线、应变能和晶格常数,获得以下主要结论:1)Fcc-Cr1-xSixN是亚稳相,具有分解为Fcc-CrN和Fcc-SiN的趋势.2)在较大成分和温度范围内,Fcc-Cr1-xSixN符合调幅分解的热力学条件.3)Fcc-Cr1-xSixN的Si含量为渗透阈值时,可能不会发生调幅分解.4)Fcc-Cr1-xSixN分解相的弹性应变能小于分离能,不会抑制Fcc-Cr1-xSixN的调幅分解. 5)Fcc-Cr1-xSixN可能经调幅分解生成Fcc-SiN.

[1]VEPREK S,REIPRICH S.A concept fo r the design of novel superhard coatings[J].Thin Solid Film s,1995,268(2): 64-71.

[2]VEPREK S,HAUSSMANN M,REIPRICH S,et al.Novel thermodynamically stable and oxidation resistant superhard coatingmaterials[J].Surf Coat Technol,1996,86-87(1):394-401.

[3]VEPREK S,N IEDERHOFER A,MOTO K,et al.Composition,nanostructure and o rigin of the ultrahardness in nc-TiN/ a-Si3N4/a-and nc-TiSi2nanocompositeswith Hv=80 to>105 GPa[J].Surf Coat Technol,2000,133-134(3):152-159.

[4]JONG H YUN PARK,WON SUB CHUNG,YOUNG-RAE CHO,et al.Synthesis and mechanical p ropertiesof Cr-Si-N coatings deposited by a hybrid system of arc ion p lating and sputtering techniques[J].Surface&Coatings Technology, 2004,188-189(6):425-430.

[5]MARTINEZ E,SANJINES R,KARIM IA,et al.Mechanical p ropertiesof nanocomposite and multilayered Cr-Si-N sputtered thin film s[J].Surface and Coatings Technology,2004,180-181(3):570-574.

[6]ZHANG R F,VEPREK S.Phase stabilitiesof self-organized nc-TiN/a-Si3N4nanocompositesand of Ti1-xSixNysolid solutions studied by ab initio calculation and thermodynamic modeling[J].Thin Solid Film s,2008,516(8):2264-2275.

[7]ZHANG R F,V EPREK S.On the spinodal nature of the phase segregation and formation of stable nanostructure in the Ti-Si-N system[J].M aterials Science and Engineering A,2006,424(7):128-137.

[8]ZHANG R F,SHENG S H,VEPREK S.Stability of Ti-B-N solid solutions and the fo rmation of nc-TiN/a-BN nanocomposites studied by combined ab initio and thermodynamic calculations[J].Acta Materialia,2008,56(16):4440-4449.

[9]VEPREK S,MARITZA GJ,VEPREK H.The fo rmation and role of interfaces in superhard nc-MenN/a-Si3N4 nanocomposites[J].Surface&Coatings Technology,2007,201(2):6064-6072.

[10]ALL INGB,RUBAN A V,KARIM IA,et al.M ixing and decomposition thermodynamics ofc-Ti1-xA lxN from firstp rincip les calculations[J].Physical Review B,2007,75(1):0451231-04512313.

[11]MA YRHOFER P H,FISCHER FD,BO¨HM H J,et al.Energetic balance and kinetics for the decomposition of supersaturated Ti1-xA lxN[J].Acta Materialia,2007,55(7):1441-1446.

[12]MAYRHOFER P H,MUSICD,SCHNEIDER JM.Ab initio calculated binodal and spinodalof cubic Ti1-xA lxN[J].App lied Physics Letters,2006,88(1):0719221-0719223.

[13]ZHANGR F,VEPREK S.Phase stabilities and spinodal decomposition in the Cr1-xA lxN system studied by ab initio LDA and thermodynam icmodeling:Comparison w ith the Ti1-xA lxN and TiN/Si3N4system s[J].Acta M aterialia,2007,55(4): 4615-4624.

[14]ALL INGB,MARTEN T,ABRIKOSOV IA,et al.Comparison of thermodynamic p roperties of cubic Cr1-xA lxN and Ti1-xA lxN from first-p rincip les calculations[J].Journal of App lied Physics,2007,102(1):0443141-0443148.

[15]SHENG S H,ZHANGR F,VEPREK S.Phase stabilitiesand thermal decomposition in the Zr1-xA lxN system studied by ab initio calculation and thermodynamic modeling[J].Acta M aterialia,2008,56(8):968-976.

[16]N IEDERHOFER A,BOLOM T,NESLADEK P,et al.The role of percolation threshold for the control of the hardness and thermal stability of super and ultrahard nanocomposites[J].Surf Coat Technol,2001,146/147(7):183-188.

First Principles on Spinodal Decomposition of Fcc-Cr1-xSixN

GAO Wei,XIE Fei
(College of Quality and Technical Supervision,Hebei University,Baoding 071000,China)

Total energies of ternary solution Fcc-Cr1-xSixN phase were calculated by first p rincip le method,and de-mixing energy and spinodal curve of Fcc-Cr1-xSixN phase were calculated.The results showed that Fcc-Cr1-xSixN is metastable and ap t to decompose to Fcc-CrN and Fcc-SiN via spinodal decomposition.The strain energy between the constituent phases was smaller than the de-mixing energy, w hich couldn’t hinder the spinodal decomposition.Spinodal decomposition could not p roceed for Si composition of Fcc-Cr1-xSixN identical to the percolation threshold.Fcc-Cr1-xSixN and decompose to Fcc-SiN via the coherent spinodal decomposition.

superhard film s;spinodal decomposition;first p rincip le

TB 453

A

1000-1565(2010)05-0508-04

2010-03-22

河北省教育厅科研计划项目(z2008304)

高巍(1980—),男,河北保定人,河北大学助教.

(责任编辑:孟素兰)