智能控制在电力系统中的应用

李彦红 杨秀菊

1.日照供电公司 山东 日照 276826

2.平原供电公司 山东 平原 253100

0 引言

近年来，随着人工智能控制理论的不断发展，以模糊技术、人工神经网络和遗传算法为代表的智能控制方法在电力系统领域得到了广泛的应用。

电力系统是由各类发电单元、输电及配电线路、及用户的负荷等一系列单元组合而成的大规模非线性动态系统，其中存在着许多十分复杂的工程计算和非线性优化问题。长期以来，电力系统自动化的研究人员一直在寻找高效可靠的方法来解决这些问题。然而仍然有许多电力系统中存在的问题无法得到快速且精确的结果。其主要原因在于:1）电力系统中的有些问题无法用精确的数学模型描述，包括不能完全用数学模型来表示反映问题实质的约束条件；2）随着问题规模和复杂程度的增加，利用现有算法和计算机条件，无法在短时间内获得满意的计算结果；3）面临的许多问题的条件具有模糊性，对于系统的了解还不够精确，此外在问题的求解过程中需要专家的知识经验，这些知识经验无法用精确的数学形式表示出来。与传统的计算方法相比，人工智能控制的方法用于求解复杂的非线性系统问题有着极大的优势。它弥补了传统方法单纯依靠数学求解的不足，解决了部分传统计算方法难于求解或不能解决的问题。下面就人工智能控制在电力系统中的应用进行阐述。

1 应用神经网络进行短期负荷预测

本文中负荷预测模型采用人工神经网络的方法，学习样本选用每周中同类型日的负荷曲线。在确定样本之前，先对原始数据进行伪数据清除处理（包括大负荷投切，远动信息中的不良数据等），并在预测出结果后，对于事先知道的较大的负荷投切等，利用专家系统的原理进行相应的修改，以便得到较精确的预测结果。

下面，对此模型的几个环节作出说明。

1）负荷模式的分类

考虑到要预测n个节点的负荷，而由于各负荷节点的休假模式各不相同，为了减小误差，本文中负荷采用七种模式，即周一到周日每日一个模式。

并将节假日处理为周日模式，节假日前一天归并为周六模式，节假日后一天归并为周一模式。

2）原始负荷记录中伪数据的清除

清除伪数据的方法，使用时间序列滤波法。

3）人工神经网络的模型

人工神经网络选用前向网络，并使用梯度法进行BP学习。

4）学习算法的流程如图。

（1）学习样本的选择

用i表示预测日所属的类型（即周i）。从历史数据库中取出本周及前四周的日负荷数据，先进行数据处理，然后用该类型日及该类型日前二天的负荷数据（共三天），作为一个学习样本。学习样本的个数需要根据节点负荷值的大小和原始数据的多少来决定。

学习和预测均按小时进行。假定现在要预测t时的负荷，学习样本为 4 个，分别用 j（j=1，2，3，4）表示，则每个样本的输入8个数据值，分别为：

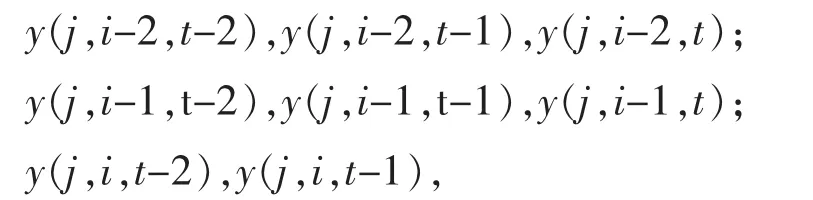
输出为一个数，即 y（j，i，t）。

（2）预测

通过样本学习确定权值后，即可进行预测。预测时输入层神经元的输入取用本周对应小时的8个数据值，其取法同学习样本，不同的是负荷数据为本周数据。此时，输出即为要预测的周i第t小时的负荷，用公式表示为：

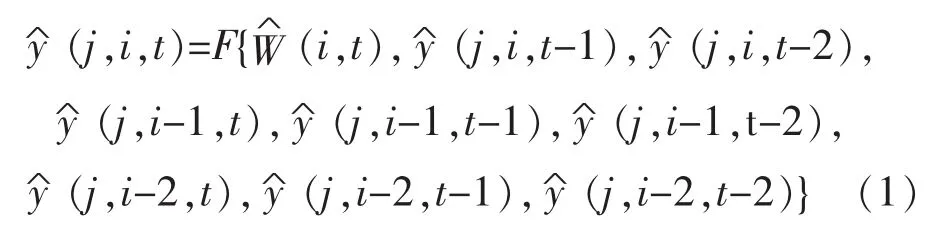
需要说明的是在学习样本和预测公式中，当预测日i为周一，预测小时t为第一小时时，i-1即为前一周的周日，i-2位前一周的周六，t-1为前一天的第24小时，t-2位前一天的23小时。预测出24小时结果后，根据事先输入的该天负荷增减信息，对负荷进行修正。

整个计算过程如图1所示。

2 基于遗传算法的无功优化

2.1 遗传算法的多途径搜索

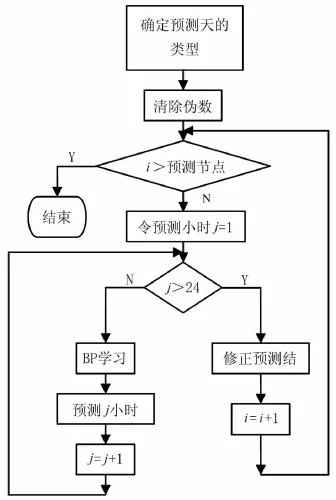
图1 负荷模型计算过程

遗传算法是一种多途径搜索的方法。为了进行多途径搜索，在每次迭代中有各种各样的条件和变量。在遗传算法中，迭代次数称为遗传代数，变量的数目被称为染色体域。在同一代中，每个中间点能相互交换信息。染色体域越大，收敛于全局最优解的可能性越大。到目前为止，虽然这种方法尚无法保证100%收敛于全局最优解，但一般情况下会收敛于全局最优解，至少其结果会比局部最优解理想。

2.2 基于遗传算法的无功优化

常规电力系统无功优化的数学模型为数学规划模型以网损最小为目标函数，以补偿电容器和变压器分接头为控制变量，以节点电压和线路潮流为安全约束。

本文中关于变压器分接头的规则采用

图2与表1为变压器分接头的操作规则。根据变压器分接头两端的电压是否满足无功优化的约束条件，可从表变压器分接头的操作规则表中对应的位置选出一个mk值来修改图中变压器分接头的相应值。表中uT和uF的相应位置取决于对应k节点的电压和允许电压的上、下限。如用ukmax，ukmin代表k节点允许电压的上、下限，则当uk＜ukmin时，相应于low位置；当ukmin≤uk≤ukmax时，相应于ok位置；当 uk＞ukmax时，相应于 high位置。

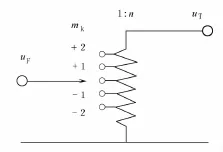
图2 变压器分接头的相应位置

表1 mk的操作规则

关于补偿电容器的规则采用:如果uk＜ukmin时，则将SC的值加1；如果uk＞ukmax，则将SC的值减1；如果ukmin≤uk≤ukmax时，则SC的值不变。

2.3 基于遗传算法的无功优化流程

1）输入待求解网络的原始数据、网络的等式约束和不等式约束。

2）将待求解变量写成码的形式，编码产生初始染色体域，其中第一代染色体的产生采用：Xi=INT［RND·（Xmaxi-Xmini+1）］+Xmini，其中，RND 为产生的唯一随机数，其范围为0≤RND≤1；INT为取整函数。

3）计算每个染色体的适应函数值。

4）用繁殖、交叉、变异三种遗传操作来完成在前代染色体域基础上产生新一代染色体域的工作。

5）对遗传操作产生的第i代染色体解码后计算其适应函数值。

6）如果遗传代数大于最先设定的最大遗传代数，结束循环；反之，返回 4）。

7）求解过程中的安全约束校验包括状态变量的等式和不等式约束，及控制变量的范围约束。如果控变量和状态变量中有违反约束的，仍需返回4）。

8）基于遗传算法的电力系统无功优化问题收敛，获得无功优化方案；方案中，染色体中适应度最好的为最优解，其次为次优，以此类推。

3 发电机电压的模糊控制

3.1 模糊变量的取得

以某电厂为例，根据现场运行人员的经验及有关专家的意见，对采样得到精确量进行模糊化，得到表2，表3和表4。

电压偏差量论域E可分为12个论域元素和8个模糊子集：

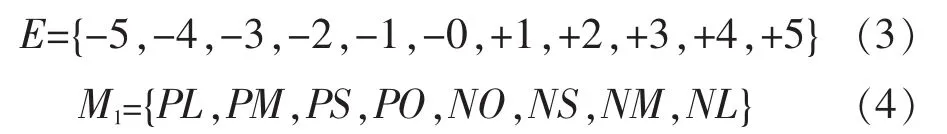
电压偏差率论域EC可分为11个论域元素和7个模糊子集：

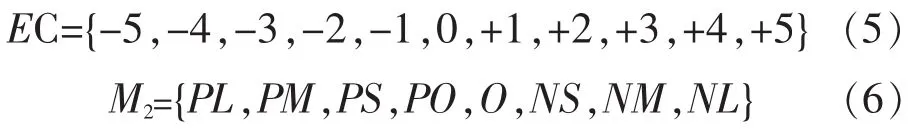
励磁控制论域F可分为15个论域和9个模糊子集：

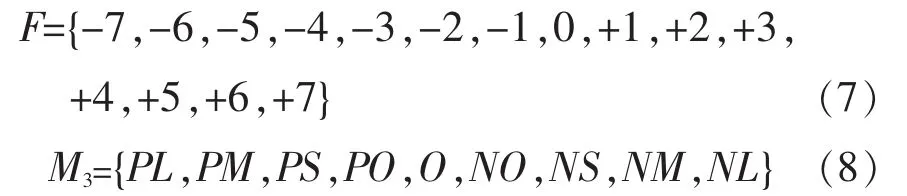
式中模糊子集的含义是：PL正大，比如电压偏差量为正切大；PM：正中；PS：正小；PO：正零；O：零；NO：负零；NS：负小；NM：负中；NL：负大。 以上各模糊子集对其论域元素的隶属度分别列于表2，表3和表4中。

表2 电压变化量的模糊子集赋值

表3 电压变化率的模糊子集赋值

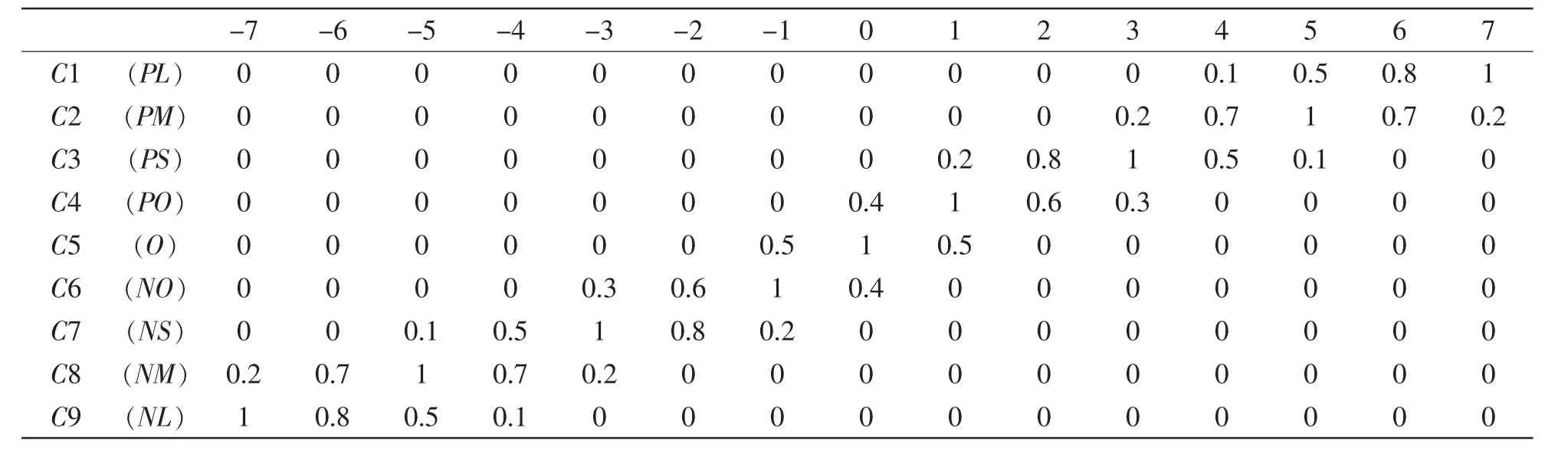
表4 励磁调节模糊子集赋值

3.2 控制规则的取得

根据实际经验，得如下推理语言规律：

“若电压误差为正中，误差变化率为正小，则励磁调节应为负中”。即对应着：

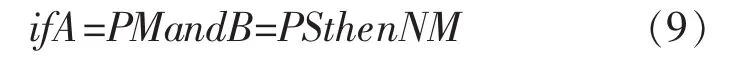
“若电压误差为正大，误差变化率为正小，则励磁调节应为负大”。即对应着：

将上述语言规则总结为控制规则表，见表5。

表5 控制规则

3.3 模糊关系得求算

根据模糊数学的运算方法，用矩阵表示if…and…then语句所包含的关系：

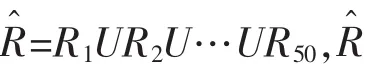
3.4 对输出信息的判决

清晰化计算时采用最大隶属度法，-7级隶属度最大，故励磁控制量应为-7级。此时-7级不再是模糊量，而是由输入的电压变化量与电压变化率经过模糊控制器得到的对励磁调节的一个判决。经计算可得控制表，如表6。

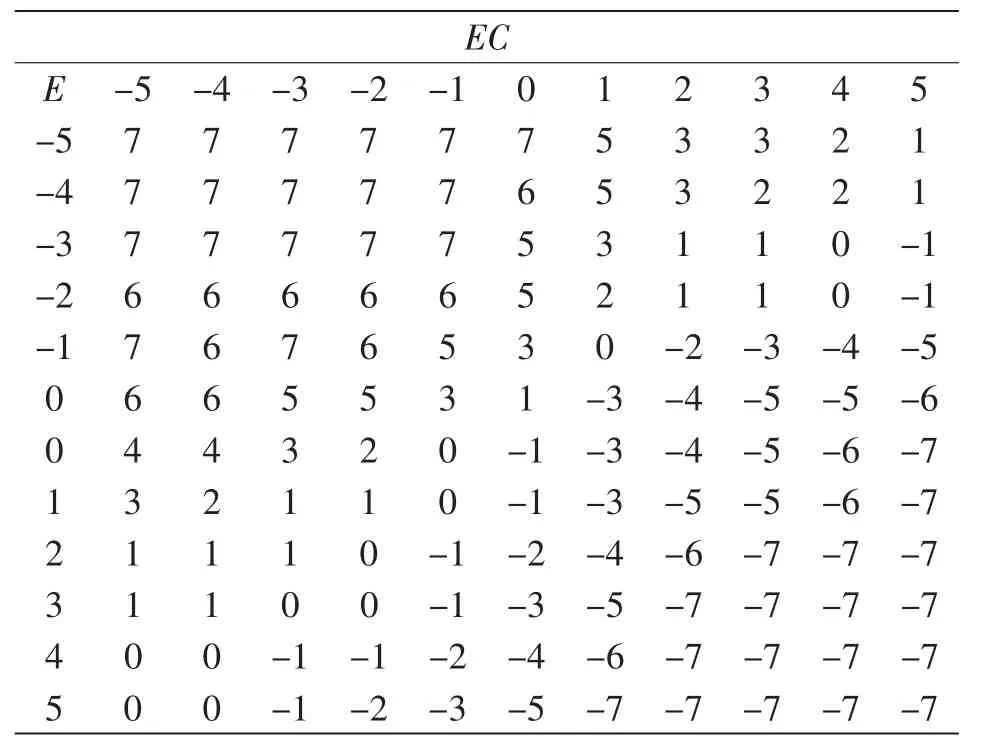
表6 励磁调节控制表

图3给出了发电机输出电压模糊控制框图。

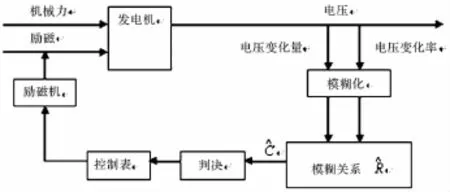
图3 发电机输出电压模糊控制框图

4 结论

神经网络控制、遗传算法和模糊逻辑控制在电力系统中已经获得了良好的应用，并日益显现出其优越性和重要性。随着我国经济的持续发展，电力系统节点数目的不断增加，数据信息量成几何倍数增长，管理上的复杂程度也在大幅度增长，以及市场竞争影响因素的加大，为智能控制在电力系统的应用提供了广阔的空间。

［1］常辉.基于遗传BP网络的智能型电力负荷预测技术[J］.电脑知识与技术，2009，（08）：1962-1964.

［2］周晓娟.电力系统无功优化方法分析［J］，中原工学院学报，2009，（01）：55-59.

［3］倪方云.采用改进BP神经网络算法预测短期电力负荷［J］.供用电，2008，（02）:16-20.

［4］张捷，王仁明，周建华.电站机组负荷分配的模糊建模及优化算法［J］.三峡大学学报（自然科学版），2009，（01）：48-51.

［5］李林川，吕东，武文杰.一种简化的电力系统负荷线性组合预测法［J］.电网技术，2002，26（10）:10-13.

［6］梁海峰，涂光瑜，唐红卫.遗传神经网络在电力系统短期负荷预测中的应用［J］.电网技术，2001，25（01）:50-53.

［7］Hagan M T，Demuth H B，Beale M H.Neural network design［M］.Beijing:China Machine Press，2002.