预报、预测和预警方法及其应用＊

赵耐青

复旦大学卫生统计学教研室上海 200032

预报、预测和预警方法及其应用＊

赵耐青

复旦大学卫生统计学教研室上海 200032

预报;预测;预警;方法学研究

目前许多企业关心自己企业的经济学和产品指标在未来的变化,医疗研究机构关心医疗指标在未来的变化,政府部门也关注国计民生的许多指标在未来的变化趋势,许多政府职能部门成立应急办公室,并且要制定预警方案和预警工作,上述工作都与预报、预测和预警方法学有关,但是许多从事这方面研究的工作人员不仅不太熟悉相应的方法学,而且往往不能区分预报、预测和预警的差异,作者就上述相关的问题,简单介绍预报、预测和预警的定义及其方法学的内容。

1 预报、预测和预警的定义

预报 (forecast)通常是估计在某个时间段或某个时期的某类观察目标将处于的状况。

预测 (predictions)一般是仅关注某类观察目标处于何种状况,一般不考虑某类观察现象将在何时处于何种状况。

例如,天气预报往往是预报某时刻的天气如何,而不会称天气预测。因此,预报至少涉及 2个要素:观察目标的状况及其出现的时间,如果要求更高的预报,则往往会涉及观察目标所出现的地点、观察目标的状况以及观察目标状况所出现的时间。如地震预报就涉及上述3个要素:地震的中心位置、地震的级别和地震发生的时间。对于疾病控制问题,有时只关注疾病会不会进展,特别是有些疾病如在初期得到控制,其以后发生进展的机会就很小了。如早期的乳癌手术患者,如果在术后 5 a内不复发、转移,则 5 a后出现复发或转移的机会就非常小,因此,乳癌手术后的患者往往关注术后是否复发或转移,而不是关注何时复发或转移,因此,评价乳癌患者术后是否复发或转移至关重要,这是对乳癌术后患者预后的预测,而不是对乳癌术后患者预后的预报。

预警 (early warning)没有统一和明确的定义,通常是根据预警目的和预警目标制定预警规则,并且定义不同的预警级别,从预报或预测所提供的信息中发现预警目标的早期信号,同时根据预警规则发出相应级别的预警信息,为早期干预或预防工作提供服务。

2 预报、预测和预警的方法

2.1 预报的方法

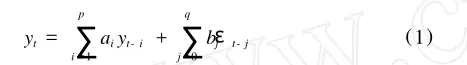
其中{εt}是独立同分布,称为白噪声,Var(εt)=σ2。ARMA模型要求时间序列{yt}的资料满足宽平稳性,即:E(yt)=μ是常数并且yt与yt+τ的自相关系数仅与τ有关,与t无关。若{εt}是正态独立同分布序列则更理想。特别当q=0时,ARMA(p,q)模型退化为下式的自回归模型 (autoregression model,AR),简称AR(p)模型:

如果时间序列不满足宽平稳性,可以对时间序列{yt}进行差分dt=yt-yt-1,t=2,3,… ,然后对{dt}应用ARMA(p,q)。如果差分后还是不满足宽平稳性,还可以进行有限次差分。差分后再应用ARMA(p,q)的模型称为ARI MA(p,d,q)模型,其中d就是对原始时间序列资料进行d次差分。由于绝大多数时间序列资料不直接满足宽平稳的条件,一般都需要进行有限次差分才满足平稳性,所以许多文献就直接应用ARI MA(p,d,q)模型进行预报。由混沌(Chaos)理论已经证明:不存在任何方法可以进行远期预报,所以AR I MA(p,d,q)模型仅可以进行有限步预报。可以证明:在ARI MA(p,d,q)模型中的yt,yt-1,…,yt-p系数构成特征方程λp-a1λp-1-…ap-1λ-ap=0的特征根的模越接近 1,则应用ARI MA(p,d,q)模型进行预报的效果会越好[3],反之特征根的模远离 1,则预报的效果就越差。由于不是每一种时间序列{yt}都满足线性预报模型,在 20世纪 90年代初,流行应用门限自回归模型 (threshold autoregression model,TAR)进行预报工作。TAR模型是对时间序列{yt}建立分段的 AR模型,这种分段的AR模型对于短期预报往往可以获得较好的预报效果。门限自回归模型一般概念介绍如下:

设{yt}为一个时间序列,则门限自回归模型的定义如下:

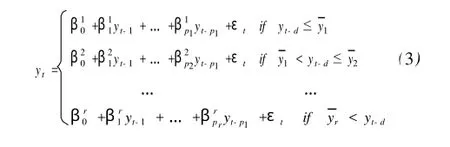
上述AR I MA(p,d,q)系列模型的建模存在一个定阶p,q,d的问题。1971年日本学者赤池(Akaike)提出了一种适用面非常广泛的统计模型选择准则,称为最小信息准则 (Akaike infor mation criterion,A IC),运用这一准则可以在模型参数极大似然估计或最小二乘法基础上估计AR I MA(p,q)模型的阶数p和q,其作法是首先引入了以下所谓的 A I C准则函数:

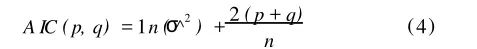
对于更一般的非线性预报模型,可以用广义线性自回归模型 (generalized linear autoregression),其定义如下:

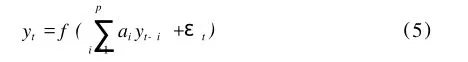
其中f()为连接函数(link function)[4]。大多数情况下,f()是由研究问题的动力学背景给定的。

对于非平稳的情况,往往采用混合时间序列模型进行分析和预报。线性的混合时间序列模型如下:

其中x1t,x2t,…,xqt为时间序列的自变量,y1,y2,…,yt为时间序列的因变量,{εt}为白噪声。特别是当上述模型退化为下列模型时,称为时间序列线性回归模型:

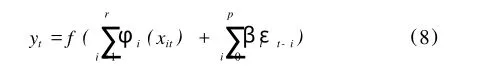
其中f()为连接函数,x1t,x2t,…,xqt为时间序列的自变量,y1,y2,…,yt为时间序列的因变量,{εt}为白噪声,φ1(),φ2(),…,φr()可以为已知函数,也可以是未知函数。对于未知函数,用样条函数(Spline function)进行拟合。目前 GAM+AR模型已经广泛应用于环境污染和气温对健康的效应评价。

2.2 预测的方法

预测方法通常就是对观察目标进行估计的技术,最普通的方法就是线性回归模型、logistic模型及对数线性模型等,这类模型对于预测而言,一般要求用于拟合模型资料中的自变量资料范围较大。如果预测的自变量在拟合模型的自变量资料范围内,则称这类预测值为内插预测值,如果预测的自变量在拟合模型的自变量资料范围外,则这类预测值为外推预测值。外推预测值需要对背景进行考证,以判断预测自变量值是否仍然在拟合模型的适用范围内,而且一般认为这种预测的误差比内插预测值的误差大,所以在一般的统计学教材中,对进行线性回归的预测往往要求自变量在拟合模型的自变量取值范围内。

绝大多数预测模型的预测值都是对反应变量的期望值进行估计,而不是对个体观察值的估计。例如单因素线性回归的预测值^y=a+bx是回归方程μy|x=α+βx中的总体均数μy|x的点估计值,而不是回归模型y=α+βx+ε中的y的点估计。对于反应变量y的估计一般只能采用区间估计。如单因素线性模型的反应变量的 95%可信区间估计为:

更一般的混合时间序列模型是在广义相加模型(generalized additive model,GAM)[5]基础上引入AR模型,具体的定义如下:

对于 Poisson回归模型 ln(E(Y))=β0+β1x1+ β2x2+…+βpxp,用样本拟合该模型后的回归系数记为b0,b1,b2,…,bp,则反应变量取值的 95%范围约为:

2.3 预警的方法

从本质上讲,预警是基于预警目的、预报或预测的可能结果,制定发出预警的规则或条例,当预报或预测的结果显示存在一定的风险时,根据事先制定的预警规则或预警条例决定是否发出合适的预警。

预警方法与预警目的密切相关,一般情况下,预警目的可以分为提示性预警和警示性预警。提示性预警主要的目的是事先做好准备工作,一般而言没有太大风险,但出现这类风险的可能性相对较大;警示性预警则表示可能的结果往往存在一定风险,需要做好预防工作,减小面临风险的可能性或者使风险造成的损失达到最小。虽然警示性预警是针对风险较大的目标,但由于风险大,所以即使发生的可能性较小,也需要发出警示,因此,可以理解为警示性预警的工作目标是及早发现面临重大风险的早期信号,并根据发生风险的早期信号发出预警。

预警又可以根据不同预警对象归为以下 3大类:①面对普通公众的预警。例如,感冒预警指数就是告诉公众患感冒的风险,起到某种提示作用,这类预警属于提示性预警,告诉公众可能面临的风险;又如:当某些地区面临某种疾病处于一定程度的流行状况时,往往需要向公众报告当前该疾病的流行状况,并且告知公众可能面临的风险大小,甚至告知更严重状况出现的可能性。这是一种警示性预警,一般需要根据事先制定的预警规则决定是否发出警示性预警。警示性预警的目的是告知公众应该采取自我保护措施,减小个体面临风险的可能性,同时提示管理部门和相关部门应做好各种预防和应对措施。②面对管理部门的预警。例如:根据天气预报,寒潮即将来临,发出预警,告知有关部门做好面临寒潮的各种准备工作,这就是提示性预警。又如:根据天气预报,近期可能会发生洪水灾害,因此事先向管理部门报告出现洪水的可能性、可能到达的时间、严重程度以及持续时间,让有关管理部门尽早作出决策并做好各种防范措施,使可能出现的洪水灾害所造成的损失达到最小。这是一种警示性预警,这种预警的风险不一定会出现,但一旦出现而没有事先做好防范准备时往往会造成重大损失。因此,即使出现这类风险的可能性很小,也需要根据预警规则决定是否发出预警。③面对专业部门的预警。例如,疟疾一般只发生在夏季,不会发生在冬季。根据现有历史资料,在冬季 1 d内发生疟疾的人数最多只有 1例,但现在某地区观察到某一天有 2例疟疾病例发生。这种结果很异常,值得专业部门做进一步的调查和研究,但没有风险,因此,应该发出提示性预警,告知各个专业部门应该密切注意这类异常情况的发展。又如:某地区从来没有出现过流行性脑炎暴发,而目前流行性脑炎的发病数已经超过了历史最高记录,虽然还没有达到暴发性流行的水平,这时根据预警规则,往往需要发出警示性预警,提示做好暴发性流行性脑炎出现的防范措施。根据现有信息,流行性脑炎呈暴发性流行的可能性非常小,作为专业部门,需要根据预警规则决定是否发出预警,决定是否应该启动高级别的监测手段和措施。

由于预警程序是基于预报或预测的结果来决定是否需要发出预警,而建立预报模型或预测模型的历史资料可能没有包含极端情况 (如:某类传染疾病的暴发性流行),因此预测或预报模型对于极端情况的预报或预测往往不太敏感,甚至出现预报和预测结果误差很大的情况,所以,在实际工作中要针对这类情况进行甄别,事先拟定预警规则。一旦出现异常情况,并且有出现极端不利情况的迹象,启动和建立异常情况的动态预报模型,进行动态建模,加强一步预报或有限步预报的精度,使预报模型动态适合极端不利情况的观察资料,提高极端不利情况的预报精度,为极端不利结局的预警提供尽可能高效准确的信息。

总之,以上的论述是基于作者从事预报、预测和预警研究工作的一些体会,可能论述的不够全面,仅供各位研究者和读者参考。

[1]Jeong HJ,HwangWT,Kim EH,et al.Statistical approaches to forecast gamma dose rates by using measurements from the atmosphere[J].Radiat ProtDosi metry,2008,131 (3):356

[2]Priestley HB.Spectral analysis and time series[M].New York:Academic Press,1981.

[3]安鸿志,陈兆国,杜金观,等.时间序列的分析和应用[M].北京:科学出版社,1983.

[4]Lindsey JK.Applying generalized linear models[M].Berlin:Springer,1997:93

[5]Dominici F,McDer mottA,Zeger SL,et al.On the use of generalized additive models in ti me-series studies of air pollution and health[J].Am J Epidemiol,2002,156(3): 193

特约述评作者简介

赵耐青,男,1954年 1月出生。教授,博士研究生导师。1983年毕业于复旦大学数学系,获理学学士学位;1996年毕业于澳大利亚 Newcastle大学,获生物统计学硕士学位。任上海市预防医学会卫生统计专业委员会主任委员、中国卫生信息学会卫生统计教学专业委员会副主任委员、中国卫生信息学会常务理事、中国卫生信息学会卫生统计理论与方法专业委员会常务理事、国家食品和药品监督管理局药品评审中心的专家数据库成员、国际临床流行病工作网成员、中国医学数学会常务理事和上海市统计学会理事。主要研究方向:医学研究中的统计方法学及其应用、时间序列分析和流行病学统计模型。作为研究骨干,参与国家“973”项目 2项;作为生物统计学研究者,参与国家“863”项目 2项和国家支撑项目 1项;作为生物统计学者,参加美国“N I H”项目 6项;目前作为主要研究者,承接国家自然科学基金资助项目《气温与上海市医院儿科门急诊人次关联性及其预测模型的研究》,项目号为30972551。在国内外杂志上发表论文 100余篇,主编和出版教育部“十·五”规划教材《医学统计学》、教育部“十一·五”规划教材《卫生统计学》和《临床研究设计和数据分析》,副主编医学统计类教材 3本,参编其他专业书籍 10余部。

＊国家自然科学基金资助项目 30972551

(2009-12-07收稿 责任编辑赵秋民)