对称边缘最大相关性图像插值算法与实现＊

汪陈伍，张崇军

（1西安邮电学院通信技术研究所，西安 710061；2中国兵器工业第203研究所，西安 710065）

0 引言

图像插值在数字图像处理中有重要的应用，包括图像缩放、图像分辨率增强［1］等，应用于视频监控、远程医疗，以及图像跟踪、图像制导等武器系统方面。传统的插值算法有最邻近插值、双线性插值、三次样条插值等。传统插值算法侧重于保持图像平滑，而损失了图像边缘部分的高频信息，常常导致图像的边缘出现模糊和锯齿等现象［2］。研究表明，人眼对图像的边缘部分特别敏感，所以图像插值后图像边缘效果影响着图像的质量。

保持图像边缘特征的插值方法［1］是利用边缘移动匹配法计算各像素点之间的相似程度来寻找边缘方向，在边缘方向进行插值。该算法一定程度减少图像边缘的锯齿，但在较为平缓的边缘仍出现锯齿。改进的边沿自适应图像缩放算法［3］是计算图像中各像素处不同边沿方向的相关度，利用模糊度和延续度进行过滤优化，得到最终边沿进行插值。该算法采用多方向判断相关性，边缘锯齿得到优化，但由于它需要对图像中每个像素进行相关度计算，运算量较大，并且参与相关度计算的像素选取上存在一定的偏向性。在此基础上，提出一种对称边缘最大相关性（symmetric edge max－relativity，SEMR）的图像插值算法。

1 SEMR图像插值算法

假定原图像为A（x，y），大小为M×N，缩放后图像为A′（x′，y′），大小为M′×N′。则x向和y向的缩放比为：scalex＝M／M′，scaley＝N／N′。为求得A′中坐标为（x′，y′）的像素值A′（x′，y′），需计算得到图A中的对应坐标为（x0，y0），则：x0＝scalex×x′，y0＝scaley×y′，由于x0、y0可能不是整数，对其进行取整，x＝［x0］，y＝［y0］。以A（x，y）周边像素为参照点，根据插值算法得到A（x0，y0）值，赋值给A′（x′，y′）。

SEMR算法对于边缘部分和非边缘部分（图像平坦区）进行不同的插值方法。在图像插值前，需要进行图像的边缘检测，取得边缘信息表。边缘检测算法［4］采用Prewitt算子（或Canny算子）实现。对于图像非边缘部分（称为平坦区），采用双线性插值，以降低计算复杂度。对于图像边缘部分，根据相关性最小准则确定边缘方向［5］，然后沿边缘方向进行插值。

1.1 对称多方向相关度计算

已知图像A的边缘信息表，并且A（x0，y0）周围4像素点为A（x，y），A（x＋1，y），A（x，y＋1），A（x＋1，y＋1），若4像素点中存在边缘，则可能需要进行相关度计算。若Gx＞Gy，为垂直边缘，反之为水平边缘。若4个像素点中存在且仅存在水平边缘，则需要进行水平方向相关度计算；若4个像素点中存在且仅存在垂直边缘，则需要进行垂直方向相关度计算。以水平边缘为例进行对称多方向相关度计算，SEMR算法相关度公式为：

式（1）、式（2）中：A（x，y）为图像中的第y行第x列像素的灰度值，Wd（α）为第y行向第（y＋1）行α方向的相关度，Wu（β）为第（y＋1）行向第y行β方向的相关度，它们是加权了的4个水平相邻像素不同边缘方向的绝对差的和。C（α）和D（β）是不同方向的加权系数，分别随着｜α｜和｜β｜的增大而减小，反应了像素间的相关性与像素间距离的一种关系。E（i）是参与和运算的4个平行方向绝对差的不同权值，距离A（x0，y0）越远，权值越小。由图1可知，α＝n和β＝－n（n＝－5，－4，…，5）在空间方向是一致的，并且α＝β＝0时，Wd（0）＝Wu（0）。当Wd（α）或Wu（β）越小时，表明该方向的相关性越大，所以目标就是找出Wd（α）和Wu（β）中最小值的方向。

文献［3］方法仅仅计算了Wd（α）［3］，参与运算的第（y＋1）行像素为14个，多于第y行的4个像素，像素点选取存在一定的偏向性，对判断结果就会产生影响。而计算Wu（β）的过程中，参与运算的第（y＋1）行像素为4个，而第y行的像素为14个。所以，将Wd（α）和Wu（β）的结果进行综合比较，并且考虑E（i）权值的影响，将能减少噪声的干扰，使结果更加准确。

1.2 确定边缘方向

边缘方向的确定，需要依靠Wd（α）和Wu（β）两组相关性数据的比较。由于噪声的存在，会出现一些假边缘方向，需要进行剔除。假定γ为边缘方向，记γ＝F（α＝n），n∈ ［－5，5］，可知γ＝F（α＝n）＝F（β＝－n）。假定α′为Wd（α）取得最小值的方向，β′为Wu（β）取得最小值的方向，则：

式中：若α′＝β′＝0，则求得的边缘方向为垂直方向，对于非垂直方向，若α′＝－β′，表明通过Wd（α）和Wu（β）计算出的边缘方向一致，则γ＝F（α＝α′）＝F（β＝β′）为最终边缘方向。对于第三种情况，即｜α′－（－β′）｜＝1时，表明通过Wd（α）和Wu（β）计算出的边缘方向存在1单位的差别，则最终边缘方向需要进行进一步判断，此时γ的值如下：

若通过Wd（α）和Wu（β）计算出的边缘方向有1单位以上的差别，表明不存在明确的边缘方向，认定为噪声，按照平坦区插值方法进行插值。

1.3 图像插值

确定存在边缘方向的边缘后，就可以进行图像插值。根据是否存在边缘方向，可以将图像分为平坦区和边缘区两个部分。对于图像平坦区选择传统插值算法，比如双线性插值或三次样条插值。对于图像边缘区沿边缘方向进行双线性插值，原理如图2所示，图中以α＝－2边缘方向为例，黑点r、s、t为待插值的目标像素点，分别代表着此方向下三种不同的情况。AF、H－M分别为第y行和第y＋1行相邻像素点。对于r点，用平行四边形EFJK进行双线性插值；对于s点，平行四边形DEIJ进行双线性插值；对于t点，用平行四边形CDHI进行双线性插值。

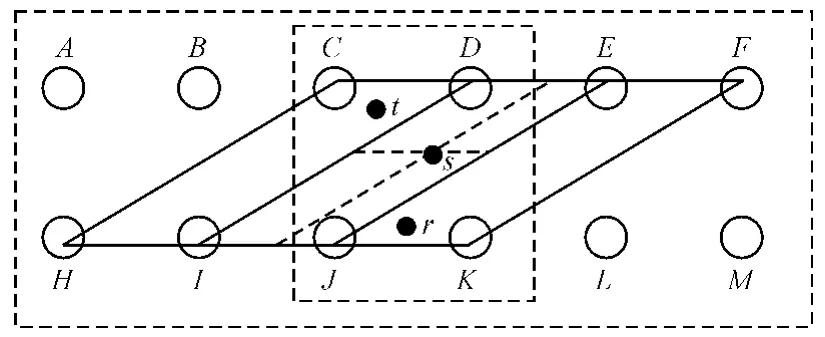
图2 按边缘方向插值原理图

1.4 算法流程

整个算法实现分为以下几个步骤：

1）采用Prewitt算子对图像进行边缘检测，得到图像边缘信息表；

2）由目标图像坐标计算，得到原图像坐标，与1）中边缘信息表进行比较，判断是否处于边缘；

3）对处于边缘的像素，需要进行对称多方向相关度计算；

4）根据3）计算结果，确定是否存在边缘方向，若存在，则确定边缘方向；

5）对于存在边缘方向的像素，按照第1.3节进行平行四边形双线性插值，对于平坦区图像采用传统双线性插值。

2 实验结果及分析

在具体实验中，计算机配置为Core2Q6600 2.4GCPU，4G内存，256M显存，在matlab7.0编程实现，选择pat图进行测试。pat图的大小为128像素×128像素，横坐标和纵坐标分别进行4倍放大，即对图像进行16倍放大。分别利用Cubic方法，文献［3］方法和SEMR算法进行对比测试，测试效果图如图3所示。可以看出，SEMR算法相对于另外2种插值方法，锯齿和边缘有一定程度的改善。

图3 Cubic方法、文献［3］方法和文中方法对比

文献［3］方法和SEMR算法运算量对比如表1所示，其中M×N为原图大小，K×L为放大后图片大小，W为原图经过边缘检测之后存在边缘的像素个数。以128像素×128像素pat图为例，W值为1568，约等于128×128大小的十分之一。当然不同的图像比例不同，处于边缘像素越少，SEMR算法的运算量相对越小。为了便于对比，两种算法的图像平坦区均采用传统双线性插值。

3 结论

SEMR图像插值算法将图像边缘检测和像素相关性计算相结合，通过对称的多方向相关度比较，确定边缘方向进行插值，有效解决图像插值后边缘的锯齿和模糊现象，相对于以往插值方法，更好抑制了边缘噪声，并且一定程度上降低了算法的运行时间，可满足图像处理实时性要求。

［1］张俊华，陈建华，王逍.基于边缘移动匹配法的图像差值［J］.计算机工程与应用，2003，39（6）：73－75.

［2］HENTSCHEL C.Generic method for 2Dimage resizing with simple，non－separable filters［C］／／International Conference on Consumer Electronics IEEE，2003：14－15，17－19.

［3］王效灵，陈涛，汪颖.边沿自适应图像缩放算法［J］.浙江大学学报：工学版，2006，40（9）：1507－1510.

［4］刘煜，李言俊，张科.一种多像素图像边缘提取方法［J］.光子学报，2007，36（2）：380－384.

［5］陈建辉，王博亮，徐中佑.一种自适应最大相关性数字图像差值算法［J］.厦门大学学报：自然科学版，2005，44（3）：355－358.