柔性作业车间多品种小批量调度算法研究

吴秀丽 李苏剑 杜彦华

北京科技大学,北京,100083

0 引言

目前,车间调度问题正朝着实用化、动态化和多目标方向发展。经典作业车间调度(job shop scheduling problem,JSP)模型由于对生产实践的假设太多,严重脱离实践,无法真正指导生产实践。柔性作业车间调度问题(flexible job shop scheduling problem,FJSP)由于放开了资源唯一性的约束,故更加贴近实际,但是其求解难度也更大。文献中研究JSP的比较多,关于FJSP的研究相对较少。1990年Bruker等[1]首先研究了FJSP。目前对此类问题的求解方法可归纳为分步法和集成法两类。分步法是由Brandimarte[2]首先提出,其基本思想是将复杂问题分解为几个子问题,以降低其复杂性。在FJSP调度中,将机器分配问题和调度问题分开考虑,这也源于FJSP调度的本质。集成法是将机器分配问题和调度问题同时解决,如Mati等[3]采用贪婪算法、Hapke[4]采用模拟退火算法、Rigao[5]和 Dauzere—Peres等[6]采用禁忌搜索法、Mastrolilli等[7]采用局部搜索法等研究都属于集成法。

由于企业的生产模式已由过去的单一品种、大批量生产模式转化为多品种、小批量的模式,因此,如果在FJSP调度问题中,考虑工件批量加工中辅助生产时间的影响,将使得研究的结论更贴近实际,对生产更有指导意义。研究证明,除了少数小规模的JSP可以精确求解外,绝大多数JSP问题都是NP难题,增加了机器可选约束和工件批量的FJSP调度优化更是NP难题。因此,本文采用集成法的思想,提出了一种标准遗传算法和小生境技术集成的混合算法求解柔性作业车间多品种小批量调度问题。

1 调度问题定义

在M台机器上加工N种工件,每种工件Jj的加工有nj道工序,nj道工序之间有工艺的先后约束,工件的每道工序可由M台机器中的多台机器加工,用Mij表示第j种工件的第i道工序可用机器集合(Mij⊆{1,2,…,M}),Oij k表示第j种工件的第i道工序可用机器k,pi jk表示第j种工件的第i道工序在第k台机器上加工需要的时间,j=1,2,…,N;i=1,2,…,nj;k=1,2,…,M 。每种工件Jj的生产批量Qj不等,如果对任意的i、j,都有Qi=Qj=1,则该问题转化为单件FJSP问题。调度的任务是在M台机器上安排个工件的加工任务,使得Makespan和安装准备成本指标同时最优,并满足一些必要的约束条件。

假设条件如下:①所有机器在t=0时刻都可用;②所有工件在t=0时刻都可被加工;③所有工件的工艺计划是固定不变的;④工序在可供选择的机器上的加工时间已确定;⑤每个工件在固定时刻只能在一台机器上加工;⑥加工是非抢占式的,工件的加工不允许中断。表1所示是一个3×4的FJSP问题描述。表1中的数字表示pijk,空白表示不能加工,每一行的数据组成集合Mij。

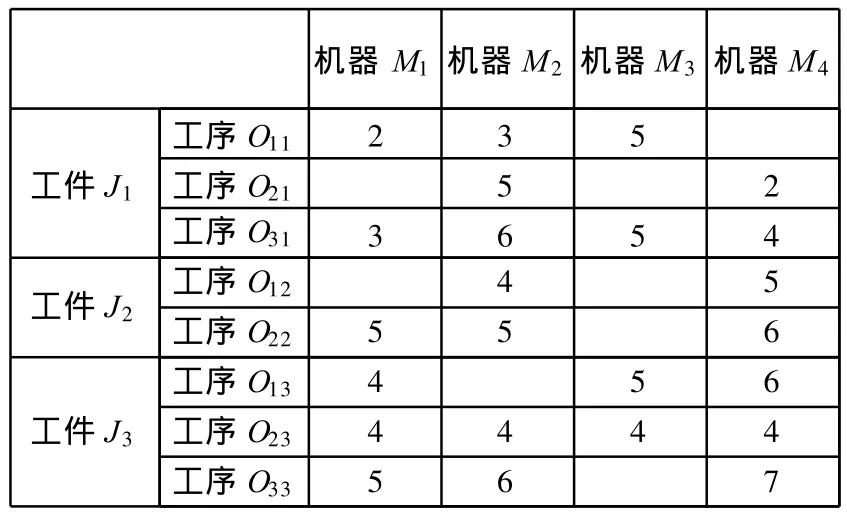
表1 3×4 FJSP问题描述

根据上述问题定义,该类问题可分为两类[3]:①完全FJSP(T—FJSP)。对于Oi j,Mij=M,表示工件Jj的i道工序可以在所有机器上加工;②部分FJSP(P—FJSP)。对于Oij,Mij⊂M,表示存在工件Jj,其第i道工序不能由全部M台机器加工。

2 基于混合遗传算法的调度优化方法

2.1 算法的总体流程图

单以Makespan进行优化,文献[8]已经给出结论,忽略生产批量,把每批中的每个工件都视为一个独立的工件安排加工,可以充分利用每台机器,使得Makespan最小。但是,现在很多加工机器是数控机床,加工不同的工件时需要很多辅助工作,如调整机床、更换夹具、刀具等,这些工作与工件类型相关,对同一种工件,只需要进行一次同样的工作。这些辅助工作需要消耗较高的安装准备成本,如果单以安装准备成本进行优化,虽然减少安装准备次数效果最好(因为成批的零件按顺序依次在一台机器上加工完毕后,再更改机器设置,加工另外一个零件,从而使得安装成本最小),但是按照文献[8]的结论,此时Makespan最大。可见这两个目标相互矛盾,无法保证两者同时最优,只能寻求两者的权衡与折中,即寻求问题的Pareto解集[9]。

本文提出集成权重系数变化法和小生境技术的混合遗传算法求解该问题。在给出算法之前,先划分两个概念:①生产批,指给定生产调度任务中的各种工件的批量,同一生产批的工件,各种加工要求和交货时间是相同的;②调度批,为了优化调度的总目标,必须将生产批分成更小的批量来安排调度,即实际参与生产的批量为调度批。可见调度批小于或等于生产批。

该类问题其实包含了两个子问题。第一个子问题是在总优化目标约束下,将工件的生产批分解为调度批;第二个子问题是对在调度批内工件的工序进行调度。这两个子问题可以分步求解,也可以同时解决,本文利用遗传算法的强大搜索解空间能力,同时解决这两个问题,算法的流程如图1所示。其中,T为最大代数。

2.2 算法的详细设计

2.2.1 编码

编码问题是设计遗传算法的首要和关键问题[10]。FJSP调度优化采用基于扩展工序的编码方式,每个染色体由N×maxnj个自然数组成,各工件均出现maxnj次。对于工序数少于maxnj的工件,多余的部分表示“虚工序”,解码时将其加工时间均设为0,而这并不影响问题本身。这种方法一方面能体现FJSP问题的机器分配特征,另一方面也是为了在以处理矩阵为特长的MATLAB仿真环境下运行而设计的。如上述3×4的例子,一个可行的编码为[2 1 1 1 2 2 3 3 3]。

这种编码方式的特点可归纳为:半Lamarkian特性;两类解码复杂性;任意基因串的置换排列均能表示活动调度;码长不小于标准长度。

2.2.2 算法参数与初始化

遗传算法最重要的参数包括:种群规模N、交叉概率C、变异概率P、最大代数T。种群规模与优化函数的性质、维数、复杂程度以及编码精度等有直接的关系。在计算量许可的情况下,要尽量选择较大规模的群体,保证群体的多样性及其进化能力,避免群体早熟现象的发生。交叉概率与变异概率的确定是个复杂的问题,其本身优化就是一个极其复杂的问题,需要经多次仿真实验得到。一般来讲,交叉概率C∈(0.4,0.9),变异概率 P∈(0.005,0.1)。最大代数 T为算法进化终止的条件。

2.2.3 解码操作

为了提高调度方案的质量,采用不同指标分别解码的方法产生多种活动化调度方案,即分别按照Makespan最小和安装准备成本最小两个指标解码,每个染色体可以得出两种调度方案。下面以Makespan最小给出解码算法。

定义1 机器顺序阵JMJM(i,j)表示加工i工件的第j道工序的机器号。用JM(i,)表示i工件的所有工序按优先顺序加工的各机器号的排列。对于FJSP问题,任意工件i的j工序可用机器数不止1个,所以该排列的长度是max(ni)×M(i=1,2,…,N),每道工序的可用机器集用M个机器号表示,称为一个子片断,P—FJSP中机器不可用时用0补齐M个子片断(机器编号从1开始)。当每个工件的总工序数不同时,取最大工序数作为子片断数,工序数少于最大工序数的工件,按照上述规则排列出机器号后,接着补齐数全为0的max(ni)—ni个子片断。从而构成维数 N×(max(ni)×M)的二维矩阵。如上述提及的3×4例子中,机器顺序阵为

定义2 加工时间阵T T(i,j)为i工件在j机器上的加工时间。对于FJSP问题,T(i,j)与JM(i,j)一一对应,当JM(i,j)是0时,T(i,j)也为0。还是上述3×4的例子,加工时间阵为

在解码之前,需进行预处理:将调度批的同类工件作为一个工件看待,调度批内的工件依次连续加工,中间不需要对机器进行重新调整参数,不耗费安装准备成本,因此,根据当前的调度批规模,修改机器顺序阵JM和加工时间阵T,即JM中的JM(i,j)中的i表示的是每个工件的调度批,j表示该调度批的工序。相应地,加工时间阵T中的每个元素T(i,j)的值由单件加工时间调整为调度批的倍数。

解码算法流程如下:①初始化工件加工工序向量,k(Ji)=1,i=1,2,…,N;②从染色体读取要加工的工件;③在JM(Ji,k(Ji))查找当前工序k(Ji)的所有可用机器序列,选择当前工序加工结束时间最早的机器,如果存在结束时间相同的机器,取加工时间较短的;④比较该机器的空闲时间段,如果工序可以插入到机器的中间空闲时间段,则转入步骤⑤,否则进步骤⑥;⑤插入该工序,并更新产品工序的当前工序结束时间,更新机器的开始时间和空闲时间;⑥在机器加工序列的末尾接着安排该工序,更新机器的当前结束时间和产品当前工序的结束时间;⑦工件Ji的工序号k(Ji)加1,返回步骤 ②,直到处理完该染色体中的所有工序;⑧结束循环,生成可行解。

算法中,工件Ji能在空闲时间段[t1,t2]插入加工的条件为

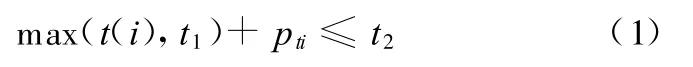
式中,t1、t2分别为空闲时间段的起点和终点;t(i)为工件Ji当前工序的最早允许加工时间;pti为工件的当前工序在选择机器上的加工时间。

当用机器安装准备成本指标解码时,解码算法与上述类似,区别在于步骤 ③中“选择结束时间最早的机器”改为选择“选择安装准备成本最小的机器”即可。

经过解码,针对当前调度批规模,每个染色体生成两种调度方案。

2.2.4 适应度计算

适应度体现了优化模型的目标函数。这里采用权重系数变化法计算个体的适应度:根据两个目标函数,每个染色体可以解码为两种方案,因此每代进化评价染色体优劣时,分别为每种方案的各目标函数赋予随机数权重,然后线性相加即为该方案的适应度,选择两种方案的适应度最大者作为该染色体的适应度。计算如下:

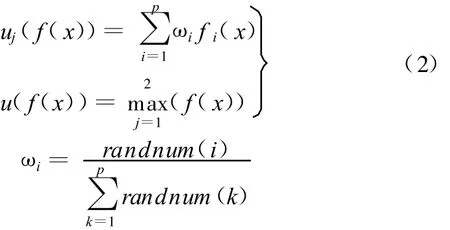
式中,p为目标函数个数;randnum(i)为随机数;fi(x)为第i个目标函数值。

2.2.5 选择操作

选择操作用于实现优胜劣汰,选择出优秀个体以较高的概率保留在进化种群中,从而提高全局收敛性和计算效率,是保证染色体不断进化的关键。这里采用轮盘赌选择方法,即设群体大小为N,其中个体i的适应度为fi,则该个体被选中的概率 Pi为

概率Pi反映了个体i的适应值在整个个体适应值总和中所占的比例,占比例越大的个体,所代表的基因结构被遗传到下一代中的可能性也越大。

为了保证优秀个体不会因为交叉变异被破坏掉,采用精英保留策略,即当前群体中的适应度最高的个体不参与交叉和变异,而是用它来替换本代群体中经过交叉、变异等遗传操作后所产生的适应度最低的个体。

另外,多目标优化的一个关键问题是保证Pareto解的多样性,因此每代进化过程中对适应度值非常接近的个体使用小生境技术[11]进行处理。小生境的构造直接影响多样性的质量,本文改进了Hyun等[11]提出的小生境环境设计方法。某个个体所在的小生境域的定义如下:以该个体为中心,由周围各边界围成一个空间,各边界大小的计算公式为

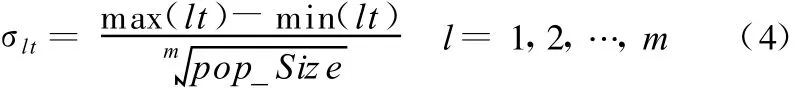
式中,max(lt)和min(lt)分别为进化到t代时第l个目标的最大值和最小值;m为目标个数;pop_Size为种群规模。

小生境域密度越小的个体被遗传下去的概率越大。图2中,个体X1比个体X2被选择的概率大。仿真过程中,发现该边界太大,淘汰掉了不应该淘汰的最优解,经过多次仿真,得到如下修正公式:

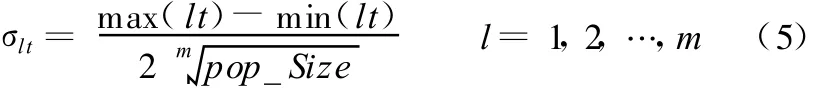
2.2.6 交叉操作

在遗传算法(GA)中,交叉操作的作用非常重要,一方面,它使原来群体中优良个体的特性能够在一定程度上得以保持;另一方面,它使算法能够探索新的基因空间,从而使新的群体中的个体具有多样性。在基于扩展工序的编码方式下,交叉操作需要特殊设计。本文采用线性次序交叉:首先随机确定两个交叉位置,并交换交叉点之间的片段,并在原先父代个体中删除从另一父代个体交换过来的基因,然后从第一个基因位置起依次在两交叉位置外填入剩余基因。如图3所示,两个父代染色体P1和P2,第一步交叉后,形成的两个子染色体C11和C12,可以看出基因有丢失和重复,按照上述方法对基因修补后得到合法的染色体C1和C2。

2.2.7 变异操作

变异操作可以帮助收敛过程跳出局部最优点,增加种群的多样性。本文采用互换操作变异方法,即随机交换染色体中两不同基因的位置。如图3染色体P1,如果变异位置选为3和6,则新的染色体变为(2 6 5 7 3 4 6 9 1)。

2.2.8 终止条件

通过设定最大进化代数T,当运行代数达到T时,进化终止。

3 仿真实验

3.1 运行环境

在Pentium 4、CPU主频为 2.13GHz、1GB内存、Windows XP操作系统下,利用 MAT LAB 6.5仿真工具编程实现上述算法。经过多次测试验证,选定的比较理想的混合遗传算法参数如下:种群大小为50,最大代数为20,交叉概率为0.6,变异概率为0.1。每台机器的安装成本数据由系统随机产生,不影响算法性能的验证。

鉴于目前国内外尚无多品种小批量柔性作业车间调度的标准算例,因此,本文分别从算法的多目标优化性能和批量调度性能两个角度进行算法性能比较分析。

3.2 算法多目标优化性能比较

对文献[12]中的 8工件、8机器,27工序的部分FJSP问题进行了仿真实验。某些工序只有部分工序可供选择。“×”表示该机器不可选,解码时将其时间置为“0”。运行10次,均在4.5s内7次得到最优解,与文献[12]中的结果进行比较,如表2所示。其中,SPT表示最短处理时间优先规则,AL表示局部搜索算法,CGA表示复合遗传算法,PSO表示微粒群算法,SA表示模拟退火算法。Makespan指标比文献中最好的结果降低一个单位,性能提高约6%,最大负荷指标比文献中的结果降低2个单位,性能提高约14%,总负荷指标略逊一筹,比最好的指标高4个单位,性能降低约5%。总体来看,该算法的性能还是相当不错,尤其在JIT生产模式中时间要求很严格的情况下,能体现其优越性。

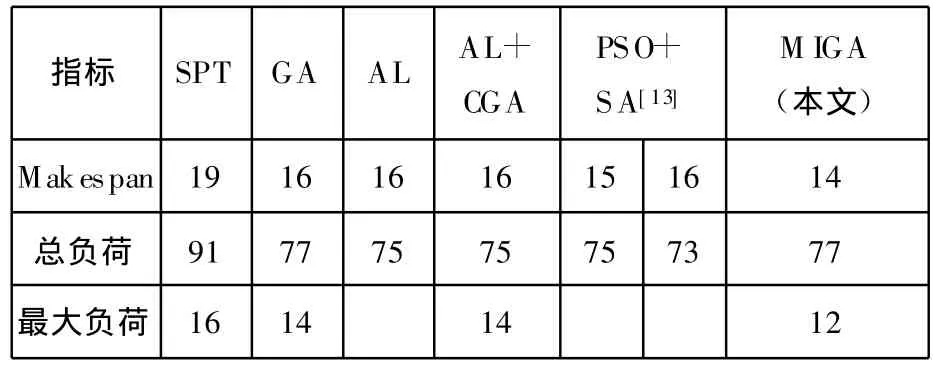
表2 针对8×8问题的不同算法结果比较

为了验证该算法求解大规模问题的性能,对文献[14]中提及的15工件、10机器、56工序的完全FJSP进行了仿真实验。运行10次,均在5.5s内6次得到表3所示的最佳结果,并与文献中的最佳结果进行了对比。从结果中可以看出,Makespan指标和最大负荷指标与文献中最好的结果一致,总负荷指标略逊一筹,比最好的指标高2个单位,性能降低约2%。

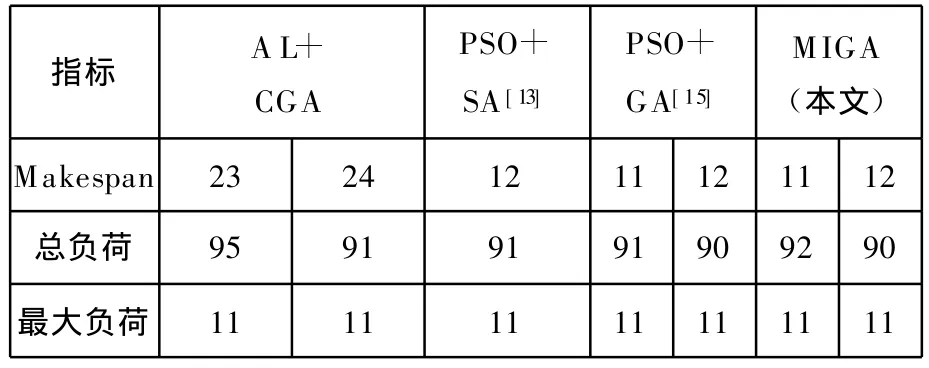
表3 针对15×10问题的不同算法结果比较

由以上两个标准算例的计算结果可以看出,本文提出的算法对于优化多目标问题可以取得良好效果。

3.3 算法批量调度性能比较

为了验证算法求解批量调度问题的性能,对文献[8]中的提及的4工件、6机器,批量为5的P—FJSP问题进行了仿真实验。运行10次,均在5s内8次得到最优解。最佳方案的甘特图见图4,甘特图中的字母表示每种工件的调度批,对应关系如表4所示,按照同一符号出现的先后顺序表示该调度批的各工序加工顺序。Makespan指标等于50,比文献[8]中提到的遗传算法得到的结果61要优越,总的安装准备成本为289。4个工件的调度批为[2,3,2,3],即工件1每2个组成1个调度批连续加工,工件2每3个组成1个调度批连续加工,工件3每2个组成1个调度批连续加工,工件4每3个组成1个调度批连续加工。不够调度批规模的剩余工件作为1个调度批单独处理。

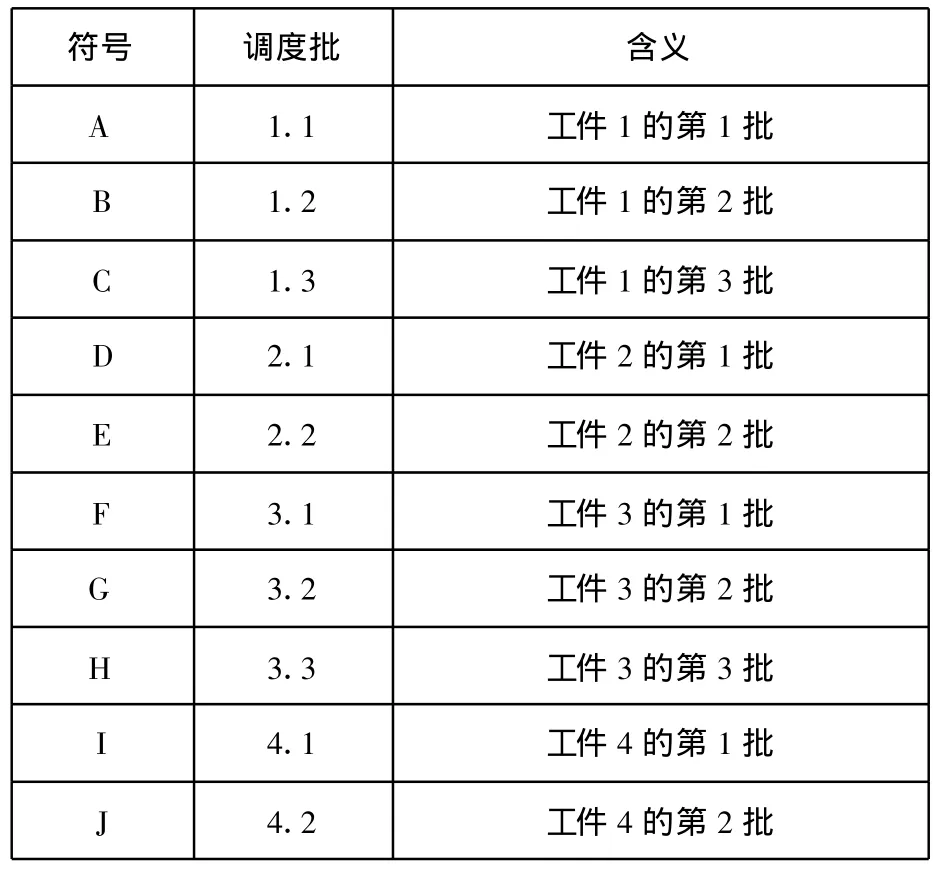
表4 调度批符号表示

4 结束语

柔性作业车间多品种小批量调度模型突破了经典JSP的可用资源唯一性限制,并把批量生产的现状考虑进来,同时面向多个指标进行优化求解,因此比单目标的经典JSP调度优化模型更符合车间调度现状,更能起到指导生产实践的作用。本文采用混合遗传算法对该类问题进行了优化求解,仿真结果证明了算法设计的合理性。目前国内外对该问题的研究较少,很多问题有待进一步研究。将来可以从三个方向展开深入研究:①进一步优化遗传算法,提高其搜索效率;②考虑采用其他方法求解该模型,如免疫算法等;③考虑更多生产实际情况。

[1]Bruker P,Schlie R.Job—shop Scheduling with Multi—purpose Machines[J].Computing,1990,45(4):369-375.

[2]Brandimarte P.Routing and Scheduling in a Flexible Job Shop by Tabu Search[J].Annals of Operations Research,1993,41(3):157-183.

[3]Mati Y,Rezg N,Xie X L.An Integrated Greedy Heuristic for a Flexible Job Shop Scheduling Problem[C]//2001 IEEE International Conference on Systems,Man,and Cybernetics.Tucson,AZ:IEEE,2001:2534-2539.

[4]Hapke M.Pareto Simulated Annealing for Fuzzy Multi—objective Combinatorial Optimization[J].Journal of Heuristics,2000,6(3):329-345.

[5]Rigao C.Tardiness Minimization in a Flexible Job Shop:a Tabu Search Approach[J].Journal of Intelligent Manufacturing,2004,15(1):103-115.

[6]Dauzere—Peres S,Paulli J.An Integrated Approach for Modeling and Solving the General M ultiprocessor Job—shop Scheduling Problem Using Tabu Search[J].Annals of Operations Research,1997,70:281-306.

[7]Mastrolilli M,Gambardella L M.Effective Neighborhood Functions for the Flexible Job Shop Problem[J].Journal of Scheduling,2002,3(1):3-20.

[8]孙志峻,乔冰,潘全科,等.具有柔性加工路径的作业车间批量调度优化研究[J].机械科学与技术,2002,21(3):348-350.

[9]Silva D L.An Introduction to Multiobjective Metaheuristics for Scheduling and Timetabling[M].Nottingham:ISN Workshop,2004.

[10]周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999.

[11]Hyun C J,Kim Y,Kim Y K.A Genetic Algorithm for Multiple ObjectiveSequencing Problems in Mixed Model Assembly Lines[J].Computers&Operations Research,1998,25(7/8):675-690.

[12]Kacem I,Hammadi S,Borne P.Approach by Localization and Multiobjective Evolutionary Optimization for Flexible Job—shop Scheduling Problems[J].IEEE T ransactions on Systems,Man and Cybernetics,Part C,2002,32(1):408-419.

[13]夏蔚军,吴智铭.基于混合微粒群优化的多目标柔性 Job—shop调度[J].控制与决策,2005,20(2):137-141.

[14]Kacem I,Hammadi S,Borne P.Pareto—optimality Approach for Flexible Job—shop Scheduling Problems:Hybridization ofEvolutionaryAlgorithms and Fuzzy Logic[J].Mathematics and Computers in Simulation,2002,60:245-276.

[15]鞠全勇,朱剑英.多目标批量生产柔性作业车间调度优化研究[J].机械工程学报,2007,43(8):148-154.