水下目标低频散射特性的波叠加解法*

程广利 张明敏

(海军工程大学电子工程系 武汉 430033)

0 引 言

散射回波蕴含着水下目标丰富的信息,可以借此判识目标的形状、尺度和材质等特性.目前目标散射问题,主要研究内容仍然是散射声场的计算方法.低频散射是当前的研究热点,也是难点所在.边界积分方程法(BIEM)因其具有降低求解空间维数、自动满足Helmholtz方程等优点,可用于研究低频散射问题,但边界积分方程法存在表面奇异积分、特征频率处解的非惟一性等不足,虽然推出了一些改进算法,可以在一定程度上解决这些问题,但其计算速度和精度等都值得探讨.

波叠加法[1](WSM)是一种间接边界积分方程方法,目前主要应用于研究声全息[2]、声辐射[3]和声源识别[4-6]、机器故障特征提取[7]等方向,本文利用波叠加法来研究水下目标低频散射特性,比较了用边界积分方程法和波叠加法求解刚性球体散射的计算结果,表明波叠加法克服了边界积分方程法的缺陷,具有计算精度高、运算速度快、适用的频率范围更宽等优点,可用于水下目标低频散射特性的研究.同时,分析表明影响波叠加法计算低频散射特性精度的因素分别是虚点源空间位置、目标表面和虚源表面划分精细程度.

1 基本理论

考虑散射体置于均质、可压缩、无粘性流体中,入射声压为

式中:P0为入射波声压幅值;k=ω/c=2πf/c为波数;ω为入射波角频率;c为水中声速;R′为坐标原点到空间任意点(x,y,z)的矢径;α,β为入射波的方位角和极角.

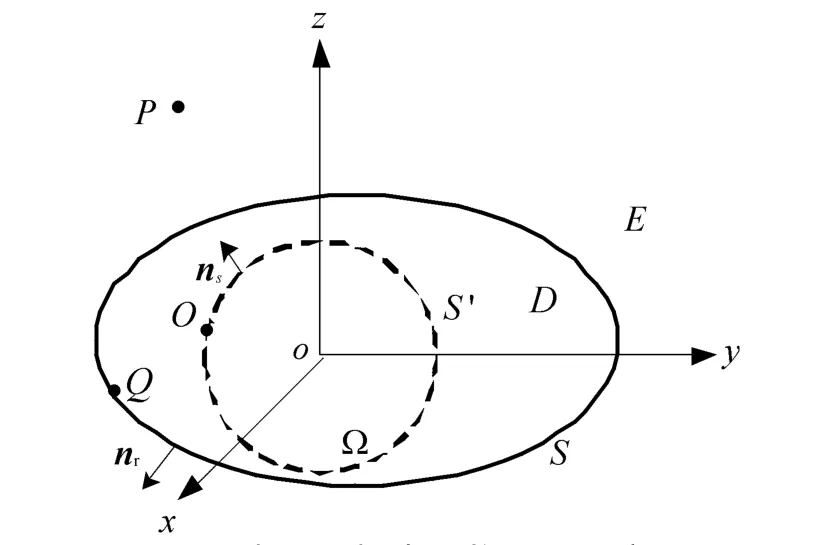
图1 水下目标声场物理量示意图

如图1所示,散射体表面S将三维空间分为内域D和外域E;P为外域E内的点,n r为表面S的外法向矢量;Q为S上的一点,Q和P间的距离为R.对于理想、均匀和静止流体中的小振幅波,声压的解为

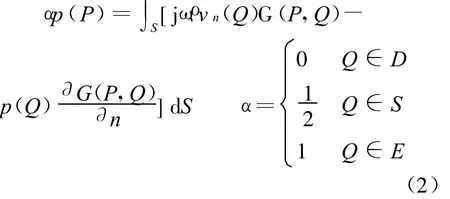
式中:ρ为流体介质密度;vn为目标表面法向振速;G(P,Q)=为格林函数.

假设在内域D内有一连续分布的声源体Ω,O为S′上的任意点;ns为S′的外法向矢量,根据质量守恒定律,可得到修正的Helmholtz方程的解为

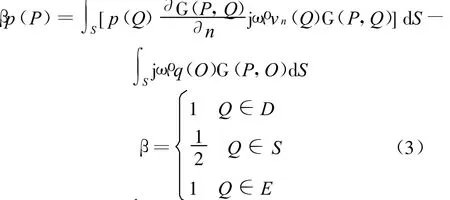
将式(2)和式(3)左右对应相加,可得目标表面外空间任意点的声压

式中:R″为P,O 2点之间的距离.

由于点P和点O不可能重合,因此不存在类似BIEM中的奇异积分问题.为避免当激励频率和虚源面S′上特征频率相等时,出现解的非惟一性问题,引入复数形式Burton-M iller型单双层混合势法,在实波数域内散射声压ps的惟一解可表示为

式中:ξ=1/k为耦合系数.由欧拉定理可知

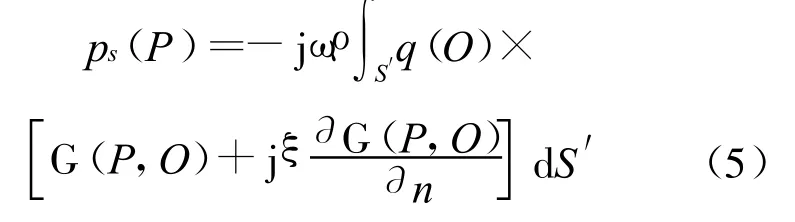
同样当P在表面S上时,可用Q代替,由式(5)可得

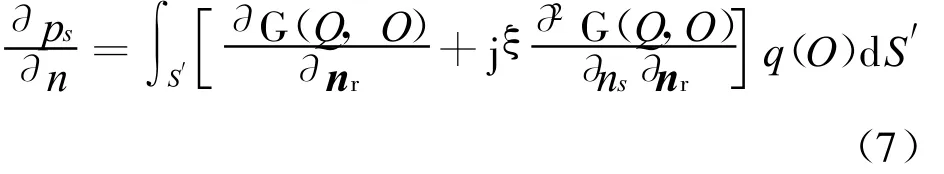
将目标表面离散成M个单元,则式(7)可表示为矩阵形式

联合式(7)和式(8)解得矩阵q,代入到式(4)中可以求得目标表面外空间某点的声压或势函数,继而求得目标表面外空间任意点的散射强度.

2 计算结果与分析

对刚性球体在海水中的后向和前向散射强度进行计算,计算相关参数设置如下:入射波为平面波,介质密度为1 040 kg/m3,声速为 1 460m/s,目标表面为理想刚性,后向散射时 α=π,β=π/2,前向散射时α=0,β=π/2,球体半径为 a,表面 S′上点源与目标表面S对应点源的距离差d=a/2,目标中心点位于坐标原点,接收点到坐标原点距离为R.归一化的计算结果如图2所示,由图可知:

1)用BIEM 计算的结果,在 附近,后向散射强度出现跃变.这是由于在特征频率附近,表面散射声压没有稳定解.当然,随着量纲一的量ka的增大,势必还会出现跃变现象.为了消除跃变的影响,可运用Helm ho ltz内部积分方程产生几个附加方程作为限制方程,便可得到正确的表面散射声压值,经上述处理后的BIEM计算结果和理论值一致性较好.

图2 刚性球体散射强度

图3 刚性球体后向散射第二个跃变值附近局部放大图

2)从图3可以看出,处理后的BI-EM 计算结果仍不如波叠加法解的精度高,且由于波叠加法不存在表面奇异积分,即使采用单双层混合势来解方程,计算时间也仅比单层势法增加50%,同等条件下其计算速度远比BIEM快.

3)同等条件下,对于刚性球体在时,刚性球体的前向散射强度大于后向散射强度,这也是其他水下目标的一个共同规律,即目标的前向散射强度通常大于其后向散射强度,可以运用这个规律来有效地探测低速运动和安静型目标,有望在探测安静型潜艇问题上得到应用,国内外已就此展开了研究[8-9].

3 影响计算精度的因素

从以上数值计算的过程可知,影响低频散射波叠加解计算精度的因素如下.1)虚源空间位置

最佳虚源面 Ω的空间位置的选择与目标表面面元有着很大的关系,应尽量使得每个面元到与自身对应面元的距离比它到除对应面元以外的其他面元间距离都要小,其目的是为了保证矩阵D的条件数尽可能的小,防止出现病态矩阵,从而影响计算结果.图4中计算了底面半径为b,高为h的刚性圆柱体归一化之后的后向散射强度,图中b′和h′分别为虚源柱体的底面半径和高,由图可知,当d=0.54 b时计算结果与理论值一致性最好,其他2种情况下精度差些,甚至无法得到正确的结果,足以可见虚源空间位置的选择对于该方法的正确应用有着举足轻重的作用,对于复杂的水下目标它是该方法应用研究的瓶颈.

2)目标表面和虚源表面划分精细程度 波叠加法本质是通过空间采样来重建声场,在每个波长内需要保证足够的面元数以满足重建精度的要求,因此在相同的条件下,将目标表面和虚源表面划分的越细,其计算精度越高,当然此时计算时间无疑会更长,应在保证计算精度的前提下,尽可能地采用数目少的面元,以提高计算速度.通常至少要保证在一个波长内有6～10个面元,而这对于低频情况下很容易满足.

图4 虚源空间位置对计算精度的影响

图5 目标与虚源表面划分精细度和波数对计算精度的影响

不同的声波波数对虚源面元划分需求自然不同,对于同一目标在小波数时面元划分可以少些,而大波数时虚源面划分则需更细.图5是上述刚性球体的理论后向散射值和波叠加法计算值的对比图,计算过程中在不同的波数时,保持划分目标表面和虚源表面数量不变,可以发现当ka达到一定的值时,用波叠加法计算的值与理论值明显误差增大,其主要原因就是当波数很大时,目标表面以及虚源体表面面元划分的不够细,使得计算结果不准确.同时可以看出,波叠加法适用的频段较宽,从理论上来说,只要在中高频时将目标表面和虚源面划分的足够小,就仍可保证计算精度,即该方法适合于所有频段,针对低频段则更有力,不需将目标表面面元划分的非常细就可以获得很高的计算精度,同时也利于提高计算速度.

4 结 束 语

分析表明,波叠加法主要思想是视目标表面外任意点处的散射声场为散射体内部的连续点源散射声场在该点的叠加,在选择合适的虚源空间位置后,根据已知声学量(阻抗、声压、振速等)计算每个虚拟面元的源强,便可求得空间中任意点的声压或势函数,进而求得散射声压.由于在数值计算过程中虚源面元与目标表面面元间距离不可能为零,且通过复数形式Burton-M iller型单双层混合势法,可在实波数域内获得惟一解,有效克服了边界积分方程的不足,分析表明该方法适合于水下目标低频散射特性的研究,影响波叠加法计算精度的因素中,虚源空间位置对其影响最明显,如何正确确定任意水下目标的虚源空间位置值得下一步去研究和探讨.

[1]向 阳,Koopman G H.基于波叠加原理的辐射声场的计算研究[J].武汉理工大学学报:交通科学与工程版,2005,29(1):1-4.

[2]李卫兵,陈 剑,毕传兴,等.联合波叠加法的全息理论与实验研究[J].物理学报,2006,55(3):1264-1269.

[3]向 宇,黄玉盈.基于复数矢径的波叠加法解声辐射问题[J].固体力学学报,2004,25(1):35-40.

[4]薛玮飞,陈 进,李加庆.机械噪声源识别的混合波叠加法[J].中国机械工程,2006,17(23):2503-2507.

[5]薛玮飞,陈 进,张桂才,等.基于混合波叠加法的声源识别理论与试验研究[J].振动与冲击,2006,25(9):1105-1108.

[6]薛玮飞,陈 进,李加庆.噪声源识别的混合波叠加法及其数值仿真研究[J].声学技术,2007,26(3):455-459.

[7]薛玮飞,陈 进,李加庆,等.机械噪声故障特征提取的波叠加法[J].机械科学与技术,2006,25(6):79-83.

[8]雷 波,杨坤德,李云飞.利用前向散射实现低速运动目标探测[C]//2007年中国声学学会青年学术会议论文集.武汉:中国声学学会,2007.

[9]Gillespie B,Rolt K,Edelson G,et al.Littoral target forw ard scattering[J],Acoustic Imaging,1997,23:501-506.