玻璃纤维增强回收聚对苯二甲酸乙二醇酯复合材料的力学性能研究

鲁 萍,吴德峰＊,邱明敏,张 明,王江洪

(1.扬州大学化学化工学院,江苏扬州225002;2.江苏省环境材料与工程重点实验室,江苏扬州225002)

玻璃纤维增强回收聚对苯二甲酸乙二醇酯复合材料的力学性能研究

鲁 萍1,2,吴德峰1,2＊,邱明敏1,2,张 明1,2,王江洪1,2

(1.扬州大学化学化工学院,江苏扬州225002;2.江苏省环境材料与工程重点实验室,江苏扬州225002)

用熔融共混法制备了玻璃纤维(GF)增强回收聚对苯二甲酸乙二醇酯(rPET)(rPET/GF)复合材料,研究了复合材料的力学性能并进一步利用 Halpin-Tsai模型、Krenchel-COX模型和 Kelly-Tyson模型探讨了 GF的近程和远程结构与复合材料性能间的关系。结果表明,GF对rPET具有较为显著的增强、增韧效果。当玻璃纤维含量为30%(质量分数,下同)时,复合材料的冲击强度、拉伸强度以及弯曲强度分别提高了245%、113%和84%;长径比和取向度是影响rPET/GF复合材料性能的重要结构参数;Halpin-Tsai方程能够较好地描述rPET/GF复合材料中GF的有效长径比;而相比于 Krenchel-COX方程,由 Kelly-Tyson方程获得的 GF的取向度更接近实验结果。

回收聚对苯二甲酸乙二醇酯;玻璃纤维;复合材料;力学性能

0 前言

作为一种最常用的性能优异的工程塑料,PET被广泛应用于纤维、薄膜、特别是中空制品等诸多领域。但大量PET中空制品尤其是饮料瓶使用后的废弃,日益加重了环境的负担,因此对 PET瓶片的回收再利用迫在眉睫。但rPET存在着特性黏度低、流动稳定性差、力学强度退化等缺点,因此研究者们常采用扩链增黏、弹性体增韧、填充增强等方法[1-3]来改性rPET,以提高其制品性能。其中,由于 GF质轻且具有优异的强度,因而采用 GF填充rPET是最常见的改性方法之一,且增强增韧的效果较为显著。众所周知,作为各向异性的填料,GF在基体中的近程和远程结构强烈影响材料的最终性能,然而围绕 GF的近、远程结构参数(长径比和取向度)与rPET复合材料性能之间定量关系的研究却相对较少。因此,本文首先制备了 GF改性的rPET复合材料,随后考察了材料的力学性能;在此基础上进一步利用力学模型建立了 GF的长径比和取向度与复合材料的宏观性能间的联系。

1 实验部分

1.1 主要原料

rPET,密度1.28 g/cm3,黏度240 Pa·s(260 ℃),上海五金大都有限公司;

GF,密度 2.62 g/cm3,直径 10μm,长径比 5000～6000,江苏南通九鼎集团。

1.2 主要设备及仪器

转矩流变仪,Polylab,美国 Thermofisher Haake公司;

液压成型机,YJ-450,余姚市华诚机械机电有限公司;

射模式制样机,RR/TSM P2,英国 Ray-Ran测试设备公司;

万能电子拉力机,WDW-5,上海华龙有限公司;

悬臂梁冲击试验机,M Z-2056,江都市明珠实验机械厂;

扫描电子显微镜(SEM),XL-30E,荷兰 PH IL IPS公司;光学显微镜,LEICA BX51,德国Olympus公司;旋转流变仪,RS600,美国 Thermofisher Haake公司。

1.3 样品制备

将rPET及GF在真空干燥箱中100℃下真空干燥10 h,充分混合后置入转矩流变仪,于255℃下共混6 min即得rPET/GF复合材料。用制样机(机筒温度260℃,模具温度110℃,注射压力0.5MPa)注射成标准样条,用于力学性能测试;用液压机于260℃,15 MPa下模压成型为1 mm厚的样片用于流变性能测试。

1.4 性能测试与结构表征

材料的冲击性能按ASTM D256进行测试,摆锤速度为3.5 m/s;

拉伸性能按ASTM D638进行测试,拉伸速率为1 mm/min;

弯曲性能按ASTM D790进行测试,弯曲速率为2 mm/min;

取rPET/GF共混材料的冲击断面,真空镀金后,采用SEM观测断面结构,加速电压20kV;

取少量样品置于烧杯中,加入足量的苯酚/三氟乙酸(体积比为1/1),80℃下恒温水浴3 h溶去rPET基体,随后取少量悬浮液滴于玻片上,真空干燥后采用光学显微镜观察 GF形态,并用Image Tool软件采集 GF的长度与直径的数据,最终数据为100个数据点的平均值,测定复合材料中 GF长径比;

将样片置于旋转流变仪的平行板夹具中(直径20 mm),升温至260℃熔融,停留3 m in以消除热历史测定试样流变性能;

稳态剪切扫描时,剪切速率0.1～100 s-1,记录黏度和剪切应力随剪切速率的变化关系。

2 结果与讨论

2.1 复合材料的力学性能

从表1可以看出,GF显著提升了复合材料的各项力学性能。当 GF含量达到30%时,复合材料的缺口冲击强度、拉伸强度以及弯曲强度分别提高了166%、113%以及84%,而弹性模量和弯曲模量分别提高了98%和544%。显然,GF具有较为显著的增强、增韧效果。从图1可以看出,当基体承载时,可以有效地将载荷传递给高强度、高模量的 GF,GF或是断裂或是拔出,在断面形成孔洞,两种方式均可以有效地耗散能量,从而产生增强、增韧作用。

2.2 复合材料中 GF的近程结构——长径比

众所周知,对于各向异性的 GF来说,长径比(λ)是其重要的近程结构参数[4]。当 GF长径比低于某一临界值时,其在基体中主要起惰性填充作用而增强效果微弱;而当 GF长径比高于临界值时,其与基体接触面积较大,因而更易与基体黏结从而有利于载荷传递使得增强效果显著。但在加工和成型过程中,GF可能会弯曲甚至断裂,因此用 GF的初始长径比(5000～6000)来评价其增强效果是没有意义的。对于聚合物填充体系,Halpin-Tsai(H-T)方程[5]建立了纤维的有效长径比与材料力学性能之间的关系:

图1 不同 GF含量的rPET/GF复合材料冲击断面的SEM照片Fig.1 SEM images fo r the impacted surfacesof the rPET/GF composites with different contents of GF

式中 Ef——GF的模量,GPa

Em——基体的模量,GPa

ξ——与填料的λ有关,对于纤维而言ξ=2λ

由于各向异性的填料还存在着彼此间的远程结构,即逾渗结构和取向分布问题,因此有学者[4]引入取向因子α来修正 GF的模量,使 H-T方程能更有效地应用于非连续纤维的填充体系,如式(3)所示。

其中,如果各向异性的填料其长度大于材料的厚度,则α=1/3;而如果填料长度小于材料的厚度,α=1/6或1/5。图2给出了采用 H-T方程拟合得到的rPET/GF复合材料拉伸强度的结果。当GF有效长径比为5时,实验值与预测值较为接近。而当 GF含量达到30%时,其强度要低于预测值,这是因为当浓度达到临界值后,GF能够相互搭接形成逾渗网络结构,从而使得单个GF对强度的贡献降低所致。显然,GF的有效长径比要远小于其初始长径比(5000～6000),这一方面是因为有效长径比本身只考虑 GF在受力方向上的力学贡献,因此与实际长径比的物理意义完全不同,其大小强烈依赖于 GF取向度;另一方面,在熔融加工过程中,GF有可能会弯曲、缠绕进而断裂,不仅减小了实际长径比,也会降低有效长径比。

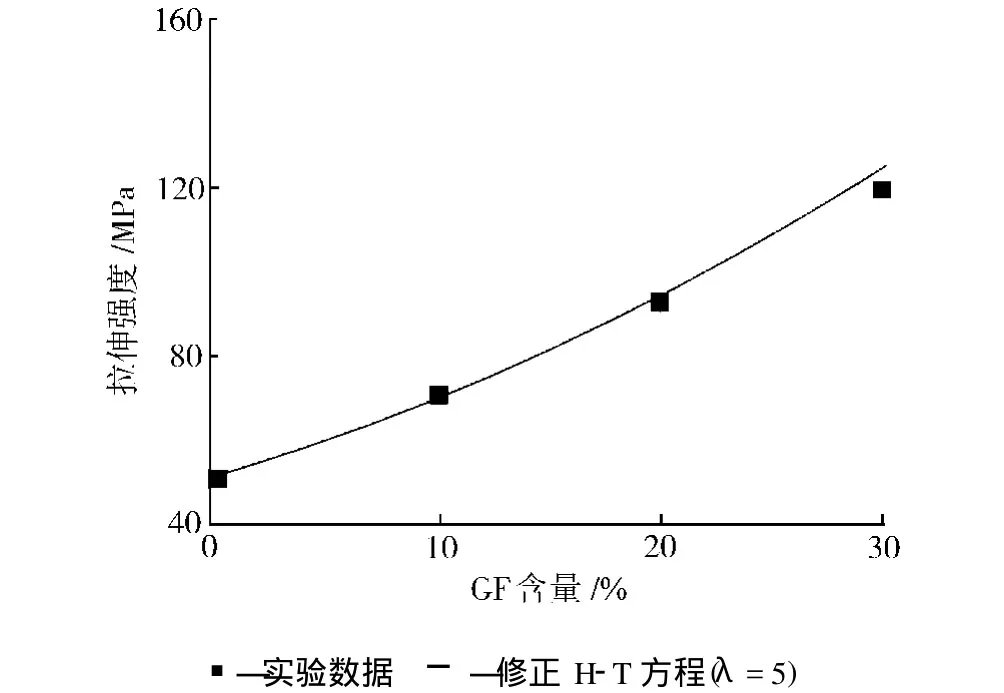
图2 H-T方程预测的复合材料的拉伸强度Fig.2 Prediction results of H-T Eq on the tensile strength of the composites

图3给出了rPET/GF复合材料中 GF的实际长度及其分布。可以看出,无论是低含量还是高含量,熔融复合后 GF的长度明显降低,其中高含量下 GF断裂程度[图3(b)]略高于低 GF含量的样品[图3(a)]。但总体而言,复合材料中 GF的平均长径比约25～30,远小于其初始长径比。这证明了熔融加工过程中 GF会发生断裂,这是复合材料中GF有效长径比不高的原因之一。

Sw itzer和 Klingenberg[6]提出了自系数(Seff)的概念用以判别聚合物填充体系中各向异性的填料是否易弯曲、断裂,如式(4)所示。

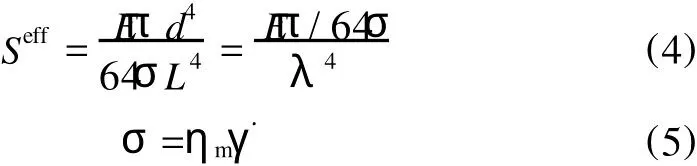
式中 L——GF的长度,mm

d——GF的直径,mm

E——GF的模量,GPa

σ——剪切应力

ηm——基体的黏度

如果 Seff→0,那么可以认为加工过程中 GF在rPET基体中是完全柔性的,可以随意弯曲;而如果 Seff→∞,那么 GF则是完全刚性的。图4给出了rPET/GF复合材料的剪切黏度。取转矩流变仪转子的平均剪切速率为 25 s-1[7],则可计算得到 GF的 Seff约为9.7×10-10。如此小的数值说明加工过程中 GF在rPET基体中非常柔顺,因此 GF的弯曲断裂不仅导致了长径比的减小,也一定程度上降低了其在复合材料中的有效长径比。但修正的 H-T方程已经将取向因子α设为定值,因此无法进一步获得复合材料中 GF远程分布的信息。

图3 不同 GF含量复合材料中 GF的长度及分布Fig.3 The length of GF and its distributions in the rPET/GF composites with different contentsof GF

图4 复合材料的黏度随剪切速率的变化关系Fig.4 The viscosity of the composites vs shear rate

2.3 复合材料中 GF的远程结构——取向度

针对非连续纤维填充具有弹性的基体,在COX模型的基础上,Krenchel[8]进一步引入了取向程度η0来修正纤维对材料模量的贡献,如式(6)所示。

式中 Gm——基体的剪切模量

Ec——复合材料的拉伸模量,GPa

Vf——GF体积分数

η1——GF长度有效因子

v——泊松比

r——GF的半径,mm

R——GF的彼此间的平均距离,mm r/R可以由Vf表示:

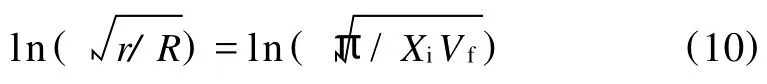
其中 Xi依赖于 GF的几何对称性,一般取值为4[9]。图5给出了 Krenchel修正后的COX模型拟合得到的rPET/GF复合材料弹性模量的结果。可以看出在较低的 GF含量下,模型预测值与实验值基本一致,由此获得的取向度值为0.004,表明 GF在rPET基体中倾向于无规分布而非择优取向。这比相关文献报导的取向度低[9],也与SEM照片(图1)中 GF的取向情况不太一致。一个可能的原因是因为COX模型只涉及了 GF和基体的模量,而并未充分考虑两者界面对强度的贡献,由此获得的取向度值自然偏低。因此,当GF含量较高时(30%),复合材料的模量高于预测值。显然,这是由于高含量下的 GF的自由转动空间变小,活动空间受限使得GF取向度上升所致。

考虑到基体与填料间的界面对复合材料强度的贡献,Kelly-Tyson[10]认为复合材料的强度主要由3项构成 ,如式(11)所示。

式中 τ——GF与基体的界面强度,τ=30 M Pa[11]

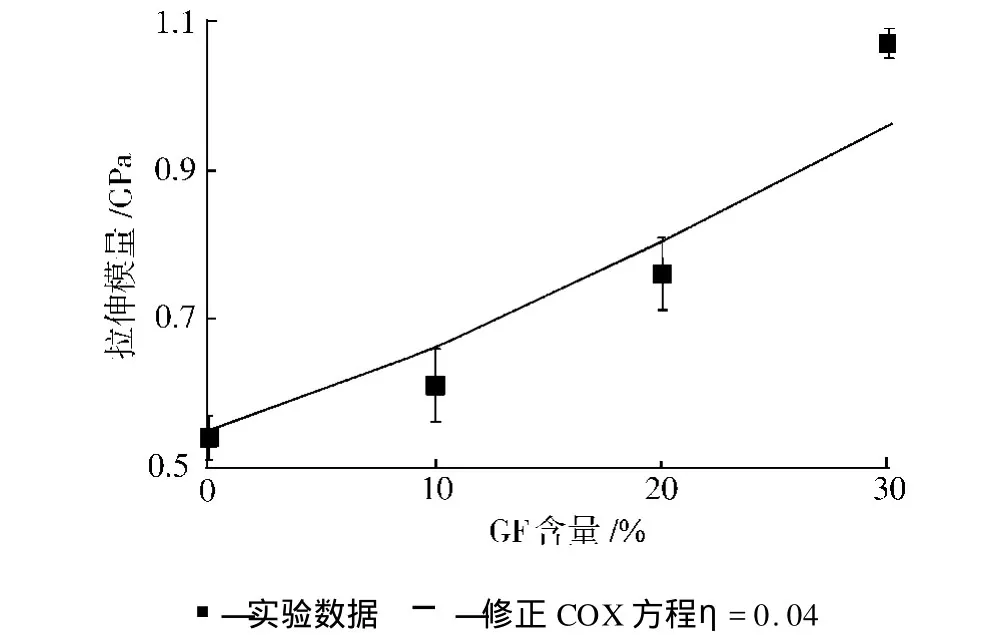
图5 Krenchel修正的COX方程预测的复合材料的弹性模量Fig.5 Prediction results of the elastic modulus fo r the composites using modified COX Eq

Vi——GF长度为 i时的体积分数

Vj——GF长度为 j时的体积分数

Lc——GF的临界长度

σfj——GF 的强度 ,取 1818 M Pa[12]

D——维维直径

σum——GF失效时基体的强度

考虑到填料对强度的贡献还强烈依赖于其远程结构,有学者[13]进一步引入取向度η修正 Kelly-Tyson模型,如式(14)所示。

图6给出了采用 Kelly-Tyson模型拟合得到的rPET/GF复合材料拉伸强度的结果。当取向因子η=0.375时,实验结果与理论计算值较接近。显然,由此获得的取向因子要比COX模型预测值更接近实际情况。但当GF含量为10%时,预测值要低于实验值,这是因为 Kelly-Tyson模型中用来表示复合材料断裂时基体本身的断裂强度值(σum)对复合材料强度的贡献偏低,甚至比纯rPET本身的拉伸强度还要低,因此预测值反而略小于实验值。而在较高的 GF含量下,预测值则稍高于实验值。一方面,从理论上来说高含量的GF一定伴随着高取向度;但另一方面,由于 GF的初始长径比远大于其临界长度,因此高含量下 GF更容易弯曲断裂,从而影响其增强效果。可见上述两者中后者起决定作用,从取向因子的数值上可判断,只有不到40%的GF在复合材料的断裂过程中做出了最大贡献。显然,作为最重要的近程和远程结构参数,长径比和取向度对于GF改性rPET至关重要。

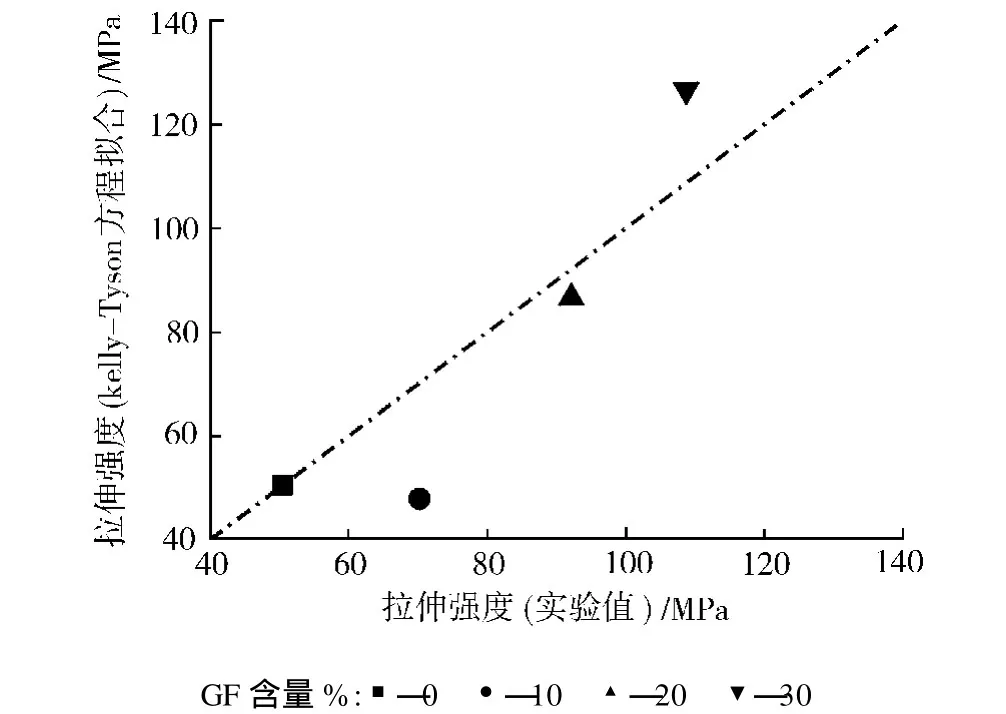
图6 Kelly-Tyson方程(η=0.375)预测的复合材料的拉伸强度与实验值的对比Fig.6 Tensile strength comparison between prediction results Kelly-Tyson Eq(η=0.375)and experimental data

3 结论

(1)GF对rPET具有较为显著的增强增韧效果;

(2)长径比和取向度是影响 GF填充复合材料性能的重要结构参数,Halpin-Tsai方程能够较好的描述rPET/GF复合材料中 GF的有效长径比;而相比于COX模型,由 Kelly-Tyson模型获得的取向度更接近实验结果。

[1] Incarnato L,Scarfato P,Maio L D,et al.Structure and Rheology of Recycled PETModified by Reactive Extrusion[J].Polymer,2000,48(18):6825-6831.

[2] Yu Z Z,Yang M S,Dai SC,et al.Toughening of Recycled Poly(ethylene terephthalate)with a Maleic Anhydride Grafted SEBS Triblock Copolymer[J].J App l Polym Sci,2004,93(3):1462-1472.

[3] Giraldi A L FM,Bartoli J R,Velasco J I,et al.Glass Fiber Recycled Poly(ethylene terephthalate)Composites:Mechanical and Thermal Properties[J].Polym Test,2005,24(4):507-512.

[4] Thomason J L.The Influence of Fiber Length and Concentration on the Properties of Glass Fiber Reinforced Polypropylene:5.Injection Molded Long and Short Fiber PP[J].Composites,2002,33(12):1641-1652.

[5] Halpin J C,Kardos J L.The Halpin-Tsai Equations:a Review[J].Polym Eng Sci,1976,16(5):344-352.

[6] Sw itzer L H III,Klingenberg D J.Rheology of Sheared Flexible Fiber Suspensions via Fiber-level Simulations[J].J Rheol,2003,47(3):759-778.

[7] Marquez A,Quijano J,Gaulin M.A Calibration Technique to Evaluate the Power-law Parameters of Polymeric Melts Using a Torque-rheometer[J].Polym Eng Sci,1996,36(20):2556-2563.

[8] Krenchel H.Theoretical and Practical Investigation of the Elasticity and Strength of Fiber-reinfo rced Material,Docto ral Thesis[D].Copenhagen:A kademisk Fo rlag,1964.

[9] Thomason J L,V lug M A.Influence of Fibre Length and Concentration on the Properties of Glass Fiber-reinfo rced Polypropylene:1. Tensile and Flexural Modulus[J].Composites,1996,27(6):477-484.

[10] Kelly A,Tyson W R.Tensile Properties of Fiber-reinfo rced Metals[J].J Mech Phys Solids,1965,13(6):329-350.

[11] Luethi B,Reber R,Mayer J,et al.An Energy-based Analytical Push-out Model App lied to Characterize the Interfacial Properties of Knitted Glass Fiber Reinfo rced PET[J].Composites,1998,29(12):1553-1562.

[12] Thomason J L,V lug M A.Influenceof Fibre Length and Concentration on the Properties of Glass Fiber-reinforced Polypropylene:4.Impact Properties[J].Composites,1997,28(3):277-288.

[13] Bader M G,Bow yer W H.An Improved Method of Production of High Strength Fiber Reinforced Thermoplastics[J].Composites,1973,4(4):150-156.

Mechanical Properties of Recycled Poly(ethylene terephthalate)/Glass Fiber Composites

LU Ping1,2,WU Defeng1,2＊,QIU Mingmin1,2,ZHANGM ing1,2,WANG Jianghong1,2
(1.School of Chemistry&Chemical Engineering,Yangzhou University,Yangzhou 225002,China;2.Jiangsu Provincial Key Laboratory of Environmental Material&Engineering,Yangzhou 225002,China)

Composites of recycled PET(rPET)filled with glass fiber(GF)were prepared viamelt mixing.The mechanical properties of the rPET/GF composites were studied through various models including Halpin-Tsai,Krenchel-COX,and Kelly-Tyson equations,aiming at exploring the relations between the short-term and long-term structures of GF and the properties of the composites.It showed that the filled GF had evident reinforcing and toughening effects on the rPET.When the GF loading was 30 w t%,the toughness,tensile and bending strengths increased by about 245 w t%,113 w t%,and 84 w t%,respectively.The aspect ratio and the orientation of GF constituted two important structural parameters vital to the final properties of the composites.The Halpin-Tsai equation could be well used to describe aspect ratio of GF.The orientation factor of GF obtained from Kelly-Tyson equation was closer to the experimental value than that from Krenchel-COX equation.

recycled poly(ethylene terephthalate);glass fibre;composite;mechanical property

TQ 323.4+1

B

1001-9278(2010)09-0084-06

2010-05-19

中国博士后基金(200902532)

＊联系人,dfw u@yzu.edu.cn