基于RCM的曲轴维修周期研究
2010-11-29魏海洲王明强
魏海洲 王明强
(江苏科技大学,江苏212003)
船舶柴油机工作时,曲轴承受着气缸内气体及往复和旋转质量惯性力引起的周期性变化的载荷,同时也受到波浪的振动与风力的影响。复杂交变的弯曲应力和扭转应力及振动共同作用在曲轴上。在这些力的作用下,曲轴容易产生疲劳破坏等各种故障,对船舶柴油机进行检验与维修可以排除因潜在的隐患造成的灾难。所以制定可靠性维修方案,对作为船舶动力心脏的柴油机的可靠性保障有着重要的经济和军事意义。
日本造船研究会和神户商船大学及船舶技术研究所在大量统计的基础上,在以可靠性为中心的维修思想(RCM)指导下,提出船机维修新构思,建立最佳维修时机的决策方法。韩帮军等指出为精确地表达设备的故障规律,工程中一般采用威布尔分布来描述电子与机械产品的故障规律。
结合设备在生产中表现出来的维修不足和维修过剩的实际现象,通过用威布尔分布,以曲轴可靠性为中心的预防性维修理论为依据,根据柴油机运行过程中检测的多种运行参数和历史信息,制定出一个保证可靠性的曲轴维修周期。
1 RCM理论
以可靠性为中心的维修(Reliability Centered Maintenance,简称RCM)是近二十年来从众多的维修理论中脱颖而出并逐步被广泛接受的一种全新的维修方法。以可靠性为中心的维修,其分析的要点,是以故障模式和故障影响分析为基础,以维修工作的适用性、有效性和经济性为决断准则,通过逻辑决断分析来确定设备的各种部件是否需要进行预防性维修工作,并确定工作类型、维修时期和维修级别[1]。
中国船级社在《船舶机械计划保养系统检验指南1997》中指出可用计划保养系统(PMS)代替规定的年度检验、中间检验和特别检验,PMS的一部分就是用状态监控技术,如振动监测、滑油分析、裂纹检测等方法,对船舶机械进行状态监测[2]。
视情维修是相对事后维修和定期维修而提出的。视情检修以设备当前的实际工作状况为依据,它通过先进的状态监测和诊断手段、可靠性评价手段以及寿命预测手段,判断设备的状态,识别故障的早期征兆,对故障部位及其严重程度、故障发展趋势做出判断,并根据分析诊断结果,在设备性能下降到一定程度或故障将要发生之前主动实施维修。它是一种建立在计算机技术、检测技术、诊断技术等多学科基础上的检修模式。
视情维修是基于这样一种事实进行的:即大量的故障不是瞬间发生的,故障从开始发生到发展成为最后的故障状态,总有一段出现异常现象的时间,而且有征兆可寻。这种在临近功能故障之前确定机件将不能完成预定功能的状态,即是潜在故障。
RCM原理包含了潜在故障的概念,用以表征设备功能故障之前的可检测或可鉴别的状态,图1表示了由潜在故障发展到功能故障的过程。A为故障开始的发生点;B为能够检测到的潜在故障点;C为实际检测到的潜在故障的检出点;D为功能故障点;T为由潜在故障发展到功能故障的间隔期。为了能在T间隔期内寻找到一个合适的维修点,引出视情维修概念。所谓视情维修就是检测机件潜在故障的工作,其目的在于发现潜在故障以便预防功能故障。由此可知,图1中的B和C之间的间隔Tc为视情维修检测间隔期。合理经济的确定Tc是有实际意义的。
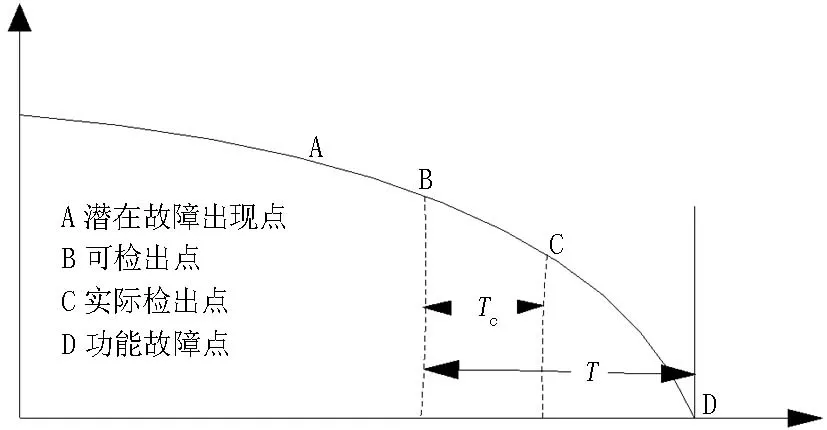
图1 潜在故障图Figure 1 Potential faults drawing
2 视情维修周期
RCM决策模型按照决策目的可以划分为:费用模型、可靠度模型、风险模型等。本文针对船舶曲轴,并且曲轴采取视情维修的方式,对RCM决策模型进行探讨与研究。在设备的维修决策中,合理确定预防维修周期对保证系统运行的效率、安全性与经济性具有重大作用。
2.1 基于可靠度的视情维修间隔模型
设故障为非工龄相关故障,从故障的后果可以确定对设备的可靠度要求,假定为R(t),而设备本身的可靠度为R′(t)。显然,若R′(t)≥R(t),则设备能够满足要求,没有必要采取预防性维修工作;若设备所能提供的可靠度R′(t)≤R(t),则必需进行预防性维修工作,其检测间隔期可按以下方法计算[2]:
设备的不可靠度F′(t)就是潜在故障发生的概率:F′(t)=1-R′(t),设备的不可靠度限制,即允许的故障概率F(t)≤1-R(t)。
如果采取预防性维修工作,故障发生的条件必须是:潜在故障发生并且没有检测到,在允许的故障概率为F(t)的条件下,所允许的潜在故障发生后未检测到的概率为:F″(t)≤F(t)/F′(t)=(1-R(t))/(1-R′(t))。
若进行一次检测能发现故障的概率为P,则所需检测次数为:n=logF″(t)/log(1-P)如果P—F时间间隔为t,则最佳预防维修周期为T=t/n
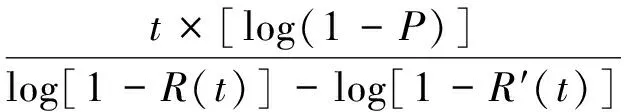
时间间隔为t可根据油液分析中的微粒数量增长数值、曲轴拐档差劣化度或裂纹发展速率来确定。
2.2 基于费用的视情维修间隔模型
总费用可分为预防维修费用和事后修理费用。预防维修费是指周期性的检查、维护、修理费;事后修理费用是指突发事故情况下修理费用。总费用最小原则是指在总费用最小情况下制定预防维修周期。
若每次检测发现故障隐患则立即更换,否则,继续使用。假定设备的故障概率密度函数为λ(t)。
设cf为一次检测所需的费用,cd为一次更换所需的费用及停机损失,cg为发生故障后修复所需费用、停机损失及故障后果费用[4],通常cd>cg。
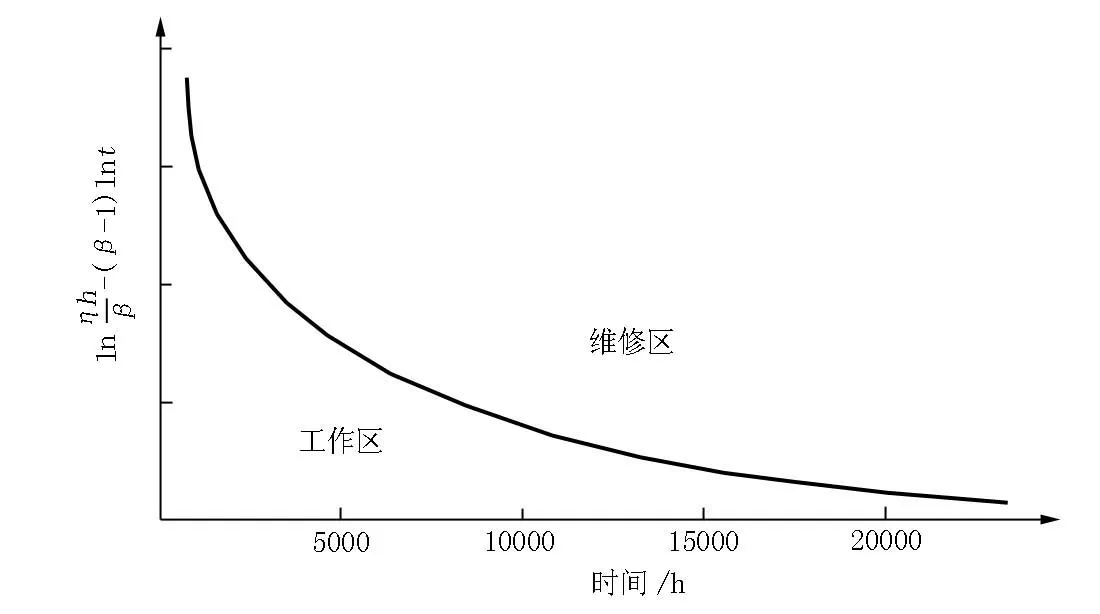
当设备寿命t满足nT 1)在故障发生前检测到潜在故障并更换所需费用为ncf+cd 2)在故障发生前没有检测到潜在故障,故障后更换所需费用为ncf+cg 在故障发生前检测到潜在故障并更换所需的平均费用: 在故障发生前没有检测到潜在故障,故障后修复的平均费用: 一个更换期内的平均费用 式中F(T)为失效分布函数,R(T)为可靠度分布函数。为了求出C最小时的维修周期T,使式(3)对时间T导数为零,确定维修总费用的驻点,该驻点对应的维修周期就是总费用最小时的维修周期。 对历史数据进行统计分析可得到C1(T)、C2(T) 的大小,式中η为尺度参数, 起缩小和放大t的作用,但不影响分布的形状,β为形状参数,决定分布密度曲线的基本形状,一旦确定了这些参数就可用数值法迭代近似求解维修周期T。 式(5)可以适当简化,因为故障损失C2(T)一般要远远大于C1(T),则可靠度可简化为: 则式(5)可简化为: 对于处于偶然故障期早期失效的的曲轴,β=1,故障率λ(t)为常数,故障服从指数分布,此时T没有合理解,预防性维修是没有意义的。 由于失效率随时间增加,所以β>1,此时定期预防维修才有意义。对于处于耗损故障期的曲轴,β>1,所求的最佳维修周期可以根据式(7)求出。 对于威布尔分布函数中参数的确定,可以采用较为简单的线性回归方法求解。某种型号8根曲轴投入运行一段时间后,均发生一定程度损坏,其中7根曲轴首次检测出裂纹时间依次为8 479 h,11 958 h,16 521 h,21 739 h,23 911 h,27 000 h,30 008 h。得出各参数点的估计值β=1.626,η=8614226,费用C1(T),C2(T)可按储存资料统计得到。 2.3 基于可用度的曲轴视情维修 曲轴是船舶维修保障的重点,采用基于状态的维修(condition basedmaintenance,CBM),即根据曲轴的裂纹、振动、滑油等状态监控情况以不等的时间间隔进行维修活动,从而避免了传统的定时维修策略(time based maintenance,TBM)带来的维修过剩或维修不足问题。 根据视情维修监测过程的适时性这一特征,引入比例风险模型(Proportional Hazards Medel,PHM)来建立视情维修数学模型,它可以把故障率和状态监控数据联合起来处理,因此把PHM引入到曲轴的视情维修决策有极大的优势[5]。 比例风险模型可以定义为与时间变量有关的失效方程: 式中,h0(t)为基本风险函数(Baseline Hazard Function),Z(t)为时间t时刻的协变量,γ′是与协变量Z(t)对应的系数,它反映了与之相对应的协变量对故障率的影响程度。其中h0(t)为: f(t)为概率密度函数,S(t)为可靠度函数。式(9)变形为: 在设备的实际运行过程中,大多数设备失效率服从威布尔分布。当威布尔分布的形状参数β=3.43954时,威布尔分布接近于正态分布;当β=1时,威布尔分布即为指数分布。由于其形状参数,使得它在数据拟合上有弹性。 所以PHM中基本风险函数可以用威布尔分布来描述,此时,PHM的表达式为: 构造极大似然函数为: 式中,H(·)代表累积风险函数,其表达式为: 式(12)中β、η和γ分别为形状参数、尺度参数和位置参数,对似然函数分别求各参数的1阶偏导数,利用数值解法如Newton-Raphson迭代法求解极大似然函数的各参数的估计值β,η,γ。 下面以最大可用度作为决策目标来建立基于比例风险模型的视情维修数学模型[6],可用度定义为系统在t时刻处于完好状态的概率,即: 式中,MTTF下为平均工作时间(即出现故障前的平均运行时间),MTTR为平均不能工作的时间。 设在每一预防周期内,平均预防性维修的时间为Tp,平均事后维修的时间为Tc,则: 式中R(T)——T时刻系统的可靠度; ((1-R(T))——T时刻系统的不可靠度。 式中f(t)——故障密度函数。 故可用度为: 令 为了得到最大可用度,通常采用对平均可用度求取极限的方法,即: 上式中的积分难以直接求出,通常采用的是数值计算方法得到不同时刻的极限可用度,其中最大极限可用度所对应的时间即为预防维修的优化时间间隔[7]。 具体数值计算过程的步骤如下[8]: (1)选择3个独立的性能参数,根据曲轴视情维修中的状态监测数据和拆换历史记录建立PHM。 (2)事后维修时间和预防维修时间的分布和状态信息可由曲轴的历史资料统计得出。选择故障数据来描点作图,将伴随变量和时间代入式(19),以时间为横坐标,绘出α-t曲线,如图2所示。 图2 可用度优化曲线Figure 2 Optimized curve of availability (3)在上述曲线中,找到α最小的点T,则此点即为平均可用度最大点。 (4)将上一步得到的T和T时刻的伴随变量值代入回归得到的PHM,求维修的故障率阈值h。 (5)根据某一相同型号设备实测数据进行决策,即要使设备的平均可用度最大,其故障率λ必须小于等于h。如果大于h就必须进行维修。即: 将式(20)两边取对数,得: z1(t),z2(t),…Zn(t)分别代表设备运行过程中监测的状态参数。将z1(t),z2(t), …Zn(t)代入上式计算,若式(21)成立,则需要在t时刻进行维修。 在实际应用中,将当前时刻监测到的各状态数据等代入式(21)计算,并在图3中描点,若该点处于曲线上方则立即采取维修措施;若处于曲线下方则继续工作。 图3 维修决策曲线Figure 3 Maintenance decision curve 基于状态的维修是建立在设备状态监测基础 上的一种先进维修方式,综合考虑设备的年龄信息和状态信息,避免了传统维修方式中的不足。PHM成功运用于CBM其中关键一点就是要找到合适的能代表设备运行状态的各种状态参数。现阶段船舶柴油机曲轴故障分析主要是在润滑油中检测金属颗粒含量信息,裂纹和振动信息等。 本文分别建立了基于RCM理论的三种不同维修目的的数学模型,提出了与曲轴维修状态信息具体结合的方法。近年来,曲轴视情维修与检验工作的重要性已得到重视,但我国在该领域的应用水平依然较低,尚存在不少问题亟待解决。 [1]贾希胜.以可靠性为中心的维修决策模型.国防工业出版社,2007. [2]船舶机械计划保养系统检验指南.中国船级社GD009-97,P1~25. [3]范英,等.船舶装备视情维修间隔模型研究.华中科技大学学报,2002(6). [4]劳立斯JF.寿命数据中的统计模型和方法[M].刘忠译.北京:中国统计出版社,1998. [5]Tsai Youtern,Wang Kuoshong,Tsai Linchang.A study of availability centred preventive maintenance for multi-component systems [J].Reliability Engineering and System Safety,2004,84:261-270. [6]Jardine A K S, Anderson P M,Mann D S.Application of the weibull proportional hazards model to aircraft and marine engine failure data[J].Quality and reliability engineering international,2007,3:77-82. [7]左洪福,张海军.基于比例风险模型的航空发动机视情维修决策.航空动力学报,2006,21(4):716-721. [8]张秀斌,等.应用比例故障率模型进行基于状态的视情维修决策. 可靠性与环境适应性理论研究,2002,4:19-22.3 模型应用


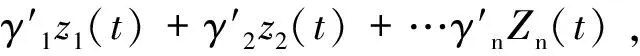
4 结论
