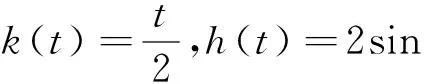Three-Point Boundary Value Problem for Second-OrderDifferential Equations with Impulses
2010-11-27YANGXuxinSHENJianhua
YANG Xu-xin,SHEN Jian-hua
(1. Department of Mathematics and Physics, Hunan First Normal University, Changsha 410205,China;2. College of Mathematics and Computer Science, Hunan Normal University, Changsha 410081,China;3. Department of Mathematics, Hangzhou Normal University,Hangzhou 310036,China)
1 Introduction
This paper, we prove existence results for the following second-order three-point boundary value problem with impulses(BVP):
(1)
whereη∈(0,1),η≠tk,α∈,J=(0,1),f∈C(J×,),0=t0 LetJ-=J{tk,k=1,2,…,m}. Denote byPC(J,) the set of functionsx:J→, such thatx(t) is continuous everywhere except for sometkat whichandexist andx(tk),k=1,2,…,m.PC1(J,)= {x∈PC(J,);x′(t) is continuous differentiable everywhere except for sometkat whichandexist, andx′(tk), fork=1,2,...,m}. ThenPC(J,),PC1(J,) are Banach spaces with the norm respectively. LetE=PC1(J,)∩C2(J-,). A functionx∈Esatisfying the BVP (1) is called nontrivial solution ifx(t)≢0. The study of three-point BVP for certain nonlinear ordinary differential equations was initiated by Gupta[1]. Over the past ten years, three-point boundary value problems have been extensively studied by many authors[2-10]. But in the existing literature on the BVP(1) is few. In a recent paper, Infante[6]investigated the BVP (1) without impulses for the first time. Boundary value problems with impulses have been studied by various authors[11-13]. The aim of the present paper is to establish some criteria of the existence of nontrivial solution for the BVP(1). Note that we do not require any monotonicity and nonnegativity conditions onf. The results we have obtained are new, and they generalize work of Sun[8]to the situation with impulses. The paper is organized as follows. In Section 2, we present two lemmas that will be used to prove the main results. In Section 3, we obtain some existence results for nontrivial solution of the BVP(1). Finally,in Section 4, as an application, we give some examples to illustrate the main results we obtain. We will start with two preliminary results. A solution of the boundary value problem (1) is called a nontrivial solution if it does not identically vanish on the unit interval. The proof of the next lemma is elementary, and we will omit it. Lemma1Lety(t) ∈PC(J,) be any solution of the boundary value problem (2) with boundary value condition. Then the three point boundary value problem (2) has a unique solution (3) Let the integral operatorT:PC(J,)→PC(J,) be defined by (4) wheret∈[0,1]. Then,by Lemma 1,the boundary value problem (1) has a solution if and only if the operator (4) has a fixed point inPC(J,). Hence,it is necessary for us only to find a fixed point ofTinPC(J,). It follows from the Arzel-Ascoli theorem thatTis a completely continuous operator. This approach makes use of following Leray-Schauder nonlinear alternative[14]. In this section, we prove our main results. Namely, we shall show that the boundary value problem with impulses (1) has at least one nontrivial solution under certain growth conditions. Theorem1Suppose thatf(t,0) is not identically zero, and there exist nonnegative functionsk,h∈L1[0,1] such that whereLk,lk,Rk,rk≥0, |f(t,x)|≤k(t)|x|+h(t) for a.e. (t,x)∈[0,1]×, and Then the BVP(1) has at least one nontrivial solutionx*∈E. Proof Write ThenA< 1. Becausef(t,0) is continuous everywhere except at {tk}×and not identically zero, there exists an interval[σ,τ]⊂[0,1] such that|f(t,0)|>0. Similarly, ash(t)≥|f(t,0)|a.e.t∈[0,1], we haveB>0. WriteM=B/(1-A),and letΩ= {x∈PC(J,):‖x‖ Theorem2Suppose thatf(t,0) is not identically zero. Then the boundary value problem(1) has a nontrivial solutionx*∈Eif the conditions below hold: (i) There exists a positive constantrsuch that Proof The condition (i) follows there exists a nonnegative functionsh∈L1[0,1] such that |f(t,x)|≤r|x|+h(t) for a.e. (t,x)∈[0,1]×andk(s)≤rfors∈[0,1].From the definition ofρ(k),ξ(k) andIk,Jk∈C(,), we obtain that there existsM1>0 such that |Jk(x)|≤ρ(k)|x|+M1, |Ik(x)|≤ξ(k)|x|+M1 forx∈. From condition (ii),letM> 0 be a sufficiently large constant such that andΩ= {x∈PC(J,):‖x‖ Hence, In this section, we give some examples to illustrate the applications of our main results. Example1Consider the three point boundary value problem with impulses (5) Example2Consider the three point boundary value problem with impulses (6) whereη≠tiandη∈(0,1). We note that Since it follows by Theorem 2 that the boundary value problem (6) has at least one nontrivial solutionx*inE. : [1] GUPTA P C. Solvability of a three-point nonlinear boundary value problem for a second order ordinary differential equations[J]. Math Anal Appl, 1992, 168:540-551. [2] FENG W,WEBB J R L. Solvability of a three-point boundary value problems at resonance[J]. Nonlinear Anal, 1997,30: 3 227-3 238. [3] FENG W,WEBB J R L. Solvability of am-point boundary value problems with non-linear growth[J]. Math Anal Appl, 1997,212:467-480. [4] GUPTA P C. A sharper condition for solvability of a three-point second order boundary value problem[J].Math Anal Appl,1997,205:586-597. [5] HE X, GE W.Triple solutions for second order three point boundary value problems[J]. Math Anal Appl, 2002,268: 256-265. [6] INFANTE G. Eigenvalues for some non-local boundary value problems[J]. Proc Edinburgh Math Soc,2003,46:75-86. [7] LIU B. Positive solutions of a nonlinear three-point boundary value problem[J]. Appl Math Comput, 2002,132: 11-28. [8] MA R. Positive solutions of a nonlinear three-point boundary value problems[J].Electronic J Differential Equations,1999,34:545-555. [9] MA R. Positive solutions of a nonlinearm-point boundary value problem[J]. Comput Math Appl,2001,42:755-765. [10] SUN Y P. Nontrivial solution for a three-point boundary-value problem[J]. Electronic J Differential Equations,2004,111:1-10. [11] DING W, RAN J, HAN M. Periodic boundary value problems for the first order impulsive functional differential equations[J]. Appl Math Comput, 2005, 165:443-456. [12] HE Z, HE X. Periodic boundary value problems for first order impulsive intergro-differential equations of mixed type[J].Math Anal Appl,2004,296: 8-20. [13] LIANG R X, SHEN J H. Periodic boundary value problem for the first order impulsive functional differential equations[J]. Comput Appl Math, 2007, 220: 498-510. [14] MING K.Nonlinear functional analysis[M].Berlin:Springer,1985.2 Preliminaries


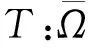
3 Main Results
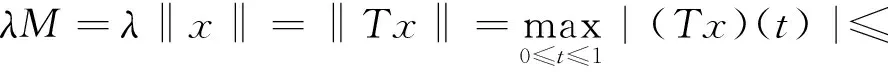


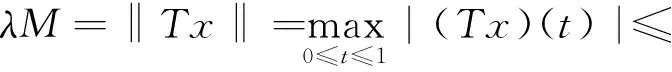
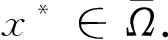
4 Examples