缝合复合材料层合板面内拉伸强度的分析

徐建新，王春水，李 强，蔡 宇

（中国民航大学航空工程学院，天津 300300）

传统的层合板复合材料在厚度方向上承受冲击载荷的能力很弱，表现出比较低的损伤容限，即在规定的维修使用周期内，传统的层合板复合材料结构抵抗由损伤导致破坏的能力比较低。另外，复合材料结构在制造过程中还会出现一些不可避免的缺陷：夹杂、空隙、纤维架桥和弯曲、局部贫脂或富脂。缝合复合材料就是为提高复合材料层合板结构的抗冲击性能，增强其层间拉伸强度而出现的一种新型复合材料结构，作为一种轻质高效结构材料，其基本力学性能的分析与预测是将该材料用于结构设计的重要前提，已成为复合材料学术界的研究热点和难点。文献[1-7]基于试验研究，探讨了缝合密度、缝合方向、缝合线半径、缝合方式等缝合参数对材料强度特性的影响。多数试验表明，缝合后拉伸强度特性有所降低，试样沿缝合针脚断裂，缝合在针脚处引起的纤维弯曲、纤维断裂等微观损伤是影响拉伸强度特性的主要因素。因此，缝合在针脚处所造成的微观损伤是决定缝合层合板抗拉强度的主要因素，但以往的强度准则和破坏指标都未能加以考虑。作为缝合层合板性能分析的基础，缝合层合板拉伸强度计算具有十分重要的意义。

笔者提出了缝合复合材料层合板抗拉强度的微观分析方法，根据相关的文献，建立了针脚处纤维局部弯曲的几何模型，该模型考虑了缝合线对缝合层合板拉伸强度的影响，同时在模型的基础上分析并计算了T700/QY8911缝合复合材料单向板的面内拉伸强度。基于单向板刚度矩阵和经典层合板理论，采用最大应力准则和强度破坏指标计算缝合层合板的拉伸强度，得到与试验数据相吻合的结果，证实了该模型的有效性。

1 拉伸强度弯曲模型

试验表明，缝合在复合材料层合板中主要造成了纤维断裂和纤维弯曲等损伤，其中，纤维弯曲是影响层合板拉伸强度的主要因素。缝合使纤维产生面内弯曲和厚度方向的弯曲，但厚度方向弯曲的纤维仅存在于层合板表层，对层合板拉伸强度的影响可忽略不计，因此仅考虑纤维面内弯曲的影响。由于层合板中各单层的铺层方向不同，所以缝合对各层造成的纤维弯曲不同，因此首先分析缝合对各单层拉伸强度的影响，然后根据经典层合板理论并采用最大应力准则和强度破坏指标得到整个层合板的拉伸强度。

单层板变形区的性质直接决定了层合板的面内力学性能。由于缝合线的加入，使得纤维绕缝线发生弯曲变形，本文提出缝合层合板面内局部纤维弯曲模型，假设缝合线受挤压后横截面为椭圆形，指出当纤维弯曲幅度较小时，缝合仅造成单胞内局部纤维弯曲，纤维弯曲角为特定值，由纤维种类决定；当纤维弯曲幅度较大时，缝合造成单胞内整体纤维弯曲，纤维弯曲角大于特定值，由纤维弯曲幅度和单胞尺寸决定。

在建立模型前，做了如下假设：①每个缝孔在层内造成的局部损伤是相同的；②纤维在面内的弯曲呈椭圆型；③铺层纤维弯曲形态沿初始铺层方向符合正（余）弦曲线；④在纤维未变形区内纤维均匀分布；⑤铺层纤维的弯曲程度是变化的，在针脚处弯曲程度最大，离针脚越远，弯曲程度越小。

一般层合板纤维的铺层有 0°、45°、90°和-45°这 4种铺层方式， 而缝合的类型一般也有 0°、45°、90°缝合这3种，但由于一般层合板的外层为0°铺层，而0°缝合相当于沿纤维铺层方向缝合，这样通常会造成纤维的分离，所以工程上通常将0°缝合改为10°，这样缝线和纤维就会有垂直、一致和成45°角3种位置关系，如图1～图3所示。

以90°缝合的单层板为例，纤维弯曲形态如图1所示。缝合针脚的均匀分布形成了周期性的单胞结构，针距为p，行距为q，缝合线半径为r。纤维按正（余）弦曲线弯曲，沿y向均匀分布，纤维最大弯曲角不小于某定值，碳纤维弯曲角不小于8.5°。

图1 缝线与纤维垂直单层板Fig.1 Stitching direction is vertical to ply′s

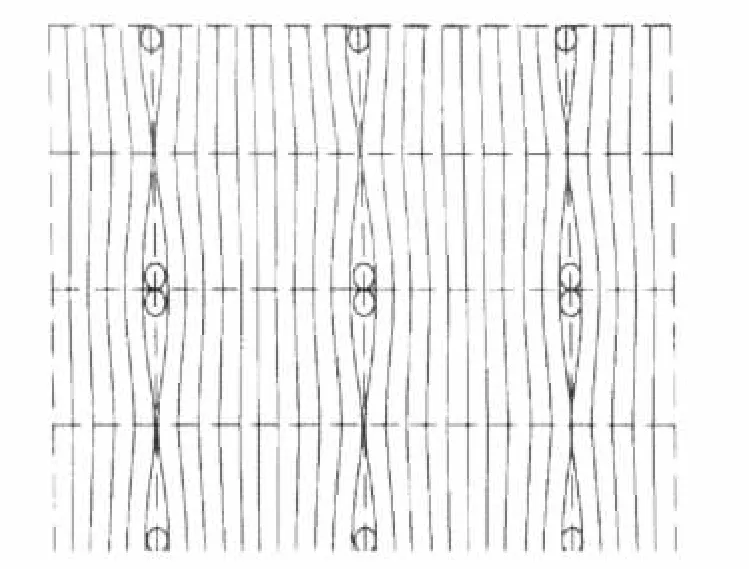
图2 缝线与纤维一致单层板Fig.2 Stitching direction is same as ply′s

图3 缝线与纤维成45°单层板Fig.3 Angle between stitching direction and ply′s is equal to 45°

单胞中的纤维形态如图4所示，关于x轴对称，单胞长为l，宽为w，纤维弯曲幅度为a，阴影区是树脂聚集区，虚线以内的非阴影区域是纤维弯曲影响区，长度为d，宽为w，虚线以外是非影响区，纤维仍为直线。

图490°缝合单层板单胞纤维弯曲型Fig.4 Model of fiber waviness in unit cell of laminates stitched in 90°direction

其中 8.5°≤ θ0≤ 20°。

纤维弯曲方程为

纤维偏转角为

纤维在各单元内近似为直线，纤维和基体混合区单元的材料可看作单向纤维复合材料，假设铺层纤维在y方向均匀排列，因此纤维体积百分含量只是x的函数，根据纤维弯曲方程可得到各单元内的纤维体积百分含量 Vf（ x）

式中，Vf0为缝合前铺层纤维的体积含量。

2 拉伸强度分析

上述的分析，已得到了单层板在变形区内纤维的偏转角和体积百分含量，由细观复合材料力学知识可计算变形区内的弹性常数和刚度矩阵，这样就得到了整个单层板的材料性质。计算出单层板的刚度矩阵，再经过叠合得到整个层合板的刚度。层合板的弹性应力应变关系为：{σ}=[Q]{ε}，其中：Q 为刚度矩阵。

采用平均刚度法确定单元体的有效弹性常数。单元体内的应变是均匀的，因而其应力—应变关系可以写为

其中Λ为整个积分区域，可分为纤维和基体两部分。采用数值积分的方法，可得到Cij的值。

这里采用经典层合板理论的基本假设（直法线假设，等法线假设，平面应力假设和忽略法向正应力假设），因此，缝合层合板面内载荷和面内变形满足物理方程[9]

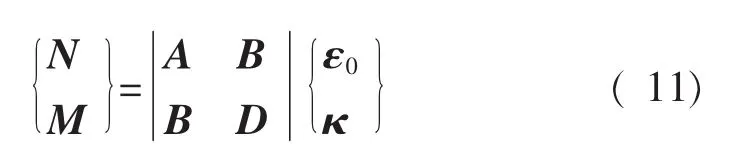
式中，A、B、D分别代表整个缝合层合板拉伸刚度矩阵、耦合刚度矩阵和弯曲刚度矩阵，它们都是3×3矩阵，由它们组成的6×6矩阵也是对称方阵，反映了一般层合板的刚度特性；ε0为中面应变向量；κ为曲率向量。Aij，Bij，Dij（i，j=1，2，6）由下式[9]确定

由于本文的材料为对称层合板即Bij=0，因此式（ 11）变为

从而层合板内任一单层的应力求得为

最后将所求得的单层主轴方向的应力分量代入最大应力准则中，计算出相应的破坏指标（F.I.）（F.I.=1表示破坏的临界状态，F.I.＜1表示尚未发生破坏，F.I.＞1表示已发生破坏。在小于1的范围内，这个值距离1越近，说明越接近破坏）。将假定的载荷值除以破坏指标中最大的一个，得到初始层破坏强度，继而重新计算层合板的刚度，继续增大载荷，进行下一步的应力分析和强度分析，这个过程反复进行，由此可以确定最终层的破坏强度。

3 预测值与试验值比较

为了验证T700/QY8911缝合复合材料层合板的拉伸性能及其强度模型的有效性，同时为了确定缝合复合材料试件的强度极限、断裂区域，在INSTRON8801电液伺服疲劳试验机上进行了试件的拉伸试验。试验中采用2 mm×3 mm的应变片，用JY-20型应变仪测量应变值。其静载误差小于1%，动载误差小于2%，夹具可以使试件自动对中，试验加载频率范围为3～20 Hz。层合板的试验环境由湿、热两种因素组成，分为干态常温、干态高温、湿态常温和湿态高温4种情况。干态是指常态；湿态是指试件在71±10℃的蒸馏水中浸泡7天。浸泡后的无缝合件的吸湿量约为1%～1.1%，缝合件吸湿量约为1.1%～1.2%。常温是指23±3℃，相对湿度为50%±10%；高温是指试件在温度为150±3℃的环境下保温至少5 min，本次所有试验均在干态常温下进行。拉伸性能试验参考载荷为 P=σs×F=σs×δ×b（ b为试件宽度、δ为试件厚度）。

试验前，测量每个试件试验段实际尺寸，根据理论计算的结果，大体估算试验所要施加的载荷；做拉伸性能试验时，在40 kN之前按每5 kN逐级加载，40 kN之后1 kN逐级加载，直至破坏，记录破坏时的载荷，计算出应力值，并观察记录试件的受力变形情况，断口形状，同时测定拉伸曲线，每组进行2个试件。

下面以[0/90]4S和[0/45/90/-45]2S两种铺层方式为例，沿90°方向缝合，材料由炭纤维T700和韧性双马QY8911树脂铺设而成。缝合纤维为Kevalr-49，缝线为1400旦尼尔（Denier）。其每层厚度为0.15 mm，其纤维体积比 V*f为 60%， 碳纤维 T700的 Ef、vf、Gf分别为230 Gpa、0.34、109.7 MPa； 树脂基体 QY8911 的 Em、vm分别为3.6 Gpa、0.30，由于基体可视为各项同性材料，于是其 Gm＝ Em/2（ 1+v）=2.34 GPa。 缝合参数为工程上常见的 p=5 mm、q=3 mm、r=0.25 mm。

为了验证强度模型的有效性，将缝合层合板模型的理论强度预测值与试验值的强度进行比较，根据上述公式计算的拉伸强度值与试验值进行对比，如表1所示。

表1 缝合层合板拉伸强度理论计算值与试验值对比Tab.1 Theoretical data and test data of strength of stitched laminates

4 结语

本文根据缝合层合板的细观几何特征，考虑因缝线穿过纤维导致纤维弯曲的近似正（余）弦曲线模型，采用最大应力准则和强度破坏指标计算了缝合层合板的拉伸强度。

通过实例计算和试验结果对比两者之间的偏差均在30%[10]以内，可见两种计算方法吻合比较好，证实了模型的正确性。

本文基于最大应力准则和破坏指标所计算出的拉伸强度，其最大特点是真实地反映了缝合复合材料层合板的细观结构实例和拉伸时的破坏情形，分析说明该模型是切实可行的。但是模型没有涉及板的初始损伤以及缝线拉力等因素的影响，没有考虑铺层厚度的影响；也没有比较缝合和未缝合层合板的面内力学性能。为了对缝合复合材料层合板面内力学性能进行更为细致的研究，有必要对模型作进一步的完善。

[1]MOURITZ A P，COX B N.A mechanistic approach to the properties of stitched[J].Composites A ，2000，31：1-27．

[2]LAMINATES KANG T J， LEE S H.Effect of stitching on the mechanical and impact properties of woven laminate composite[J].Comp Mater，1994，28：1574-1587.

[3]JAIN L K，DRANSFIELD K A，MAI Y-W.On the effects of stitching in CFRPs-II， mode II delamination toughness[J].Comp Sci Technol，1998，58：829-837.

[4]MOURITZ A P， JAIN L K.Further validation of the Jain and mai models for interlaminar fracture of stitched composites[J].Comp Sco Tech，1999，59：1653-1662.

[5]李 晨，许希武．缝合复合材料层板抗拉强度的预测[J]．机械工程材料，2006，30（ 9）：9-12.

[6]徐建新，许 健，卿光辉.缝合复合材料单层板的弹性常数分析[J].中国民航大学学报，2007，25（ 5）：5-52.

[7]魏玉卿，张俊乾，汪 海，等．缝纫复合材料层合板面内性能的分析模型[J]．重庆大学学报，2002，25（ 12）：35-38.

[8]沈观林，胡更开.复合材料力学[M].北京：清华大学出版社，2006：115-222.

[9]陈建桥.复合材料力学概论[M].北京：科学出版社，2006：33-76.

[10]沈 真.复合材料结构设计手册[M].北京：航空工业出版社，2001：573－595.