论三元数及其性质

王俊龙

(上海师范大学中国传统思想研究所,中国 上海 200234)

实数域R上的可除代数只能是实数域、复数域或四元数除环(Frobenius 1878)[1]．尚未有发现三元数的文献报道或记载．已有三元数的研究有其名而无其实，比如，下列所谓的三元数[2]：M=aE+bJ+cK,其中J2=K，K2=J，JK=E．

显然，复数不是这种“三元数”的子数系．是否存在一种三元数，以复数为其子数系？答案是肯定的．三元数具有不同寻常的性质，因而难以发现．本文初步论述三元数及其性质，关于三元数的发现则与集合的性质有关，容另文发表．

1 三元数的存在

定理若S=a+bi+cφ为三元数，则i2=-1，φ2=-i，iφ=i+φ,其中a，b，c为实数．

证若S=a+bi+cφ构成三元数，则其遵循加法和乘法运算规则．设S=a+bi+cφ和S′=a′+b′i+c′φ是任意两个三元数，那么，适用加法和乘法规则：

加法：S+S′=a+b+(a′+b′)i+(c+c′)φ．

其中，a+b是常元1的系数，a′+b′是虚元i的系数，c+c′是玄元φ的系数．三元数加法是对应元系数相加．

乘法：S·S′=aa′-b′b+(ab′+a′b+c′b+b′c-c′c)i+(ac′+a′c+c′b+b′c)φ．

其中，aa′-b′b是常元1的系数，ab′+a′b+bc′+b′c-cc′是虚元i的系数，ac′+a′c+c′b+b′c是玄元φ的系数．

三元数关于上述加法和乘法是闭的．证毕．

2 三元数的性质

三元数既有通常的代数性质，又有不同寻常的数理性质．

2.1 交换律

三元数加法和乘法遵循交换律．S+S′=S′+S，SS′=S′S．

2.2 分配律

三元数遵循乘法对加法分配律．SS′=a′S+b′Si+c′Sφ，kS=ka+kbi+kcφ．其中k为实数．

2.3 扩展性

三元数a+bi+cφ是复数a+bi的扩展．当c=0，a+bi+cφ=a+bi．

2.4 三元数常用公式

三元数平方差公式：S2-S′2=(S+S′)(S-S′)

三元数平方公式：(a+bi+cφ)2=a2-b2+(2ab+2bc-c2)i+(2ac+2bc)φ．

2.5 关于消去律

设三元数：S1=-1+i+φ，S2=1-i+φ，S3=1+i+φ，S4=1+i-φ，不难得知上述4个三元数的平方值分别如下：

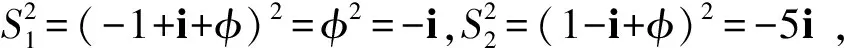
根据三元数平方差公式：S2-S′2=(S+S′)(S-S′)，不难得知

2.6 关于模法则

实数、复数和四元数遵守模法则，但是，三元数不遵守模法则．

2.7 关于方程

虚数i是方程x2+1=0的根，但是，虚元i和玄元φ不是一元二次方程的两个根．换言之，尽管iφ=i+φ，但是，韦达定理对于i和φ不成立．

上述性质6，7说明，三元数具有不同寻常的性质，也是三元数不易被发现的原因．

参考文献：

[1] 张广祥.抽象代数──理论、问题与方法[M].北京：科学出版社，2006．

[2] 王诗杰.三元数概要[J].扬州教育学院学报,2004,22(3)：10-13．