铁磁体半导体混杂纳米结构中的巨磁阻效应

刘 宇，张兰兰

(湖南第一师范学院数理系, 中国 长沙 410002)

在过去的几十年，人们一直在寻求大的磁阻效应，特别是巨磁阻效应(GMR)[1]，主要是由于其在磁信息存贮方面具有重要的实际应用，比如，超灵敏的磁传感器、磁头和随机存储器．通常，观察GMR的结构为被一薄非磁层分隔的两磁层系统．而且，在这样的异质系统中，其GMR效应是通过系统在外转换磁场下，由平行磁化构型变成反平行磁化构型时电阻的显著变化来表征的[2]，即磁阻比率MR．对于一个具体的GMR器件，从实际应用的观点出发，人们希望在相对低的转换磁场下其拥有高的磁阻比率．

为了得到大的磁阻比率MR，一条有效的途径是利用所谓的磁纳米结构，其为铁磁材料和半导体的混杂，其中磁性材料提供不均匀的磁场局域地影响半导体中电子的运动．Nogaret等证实[3]，在低温下这种纳米系统拥有GMR效应；Overend等观察到了在4 K下磁阻比率高达103%[4]．在周期磁场中，由于二维电子气(2DEG)内部Landau带结构引起的GMR振荡也可以观察到[5]．此外，人们普遍认为，平行和反平行构型的电导差异是由与自旋相关的电子散射产生．

但是，在磁调制2DEG纳米系统中与电子自旋无关的GMR效应最近被提出[6-8]．使用在2DEG上的单一函数磁垒，Zhai等[6]提出了一个GMR器件，他们发现：这种GMR效应不仅没有使用自旋自由度(其不同于常规的GMR器件)，而且虽然平均磁场为零但是这种纳米系统具有很高的磁阻比率(其高达106%)．Yang等[7]研究了在周期磁场调制下2DEG系统的GMR效应，并发现这样的周期调制纳米系统的磁阻比率与磁势的空隔及周期数密切相关．基于δ磁垒，另一个GMR器件由Papp等[8]提出，他们还考虑了该器件的磁阻比率与温度的关系．

在这篇文章中，我们研究在一般的铁磁体和半导体混杂纳米系统中的GMR效应，这里真实的磁场轮廓代替在文献[5]中的δ函数磁垒，并假设磁条的磁化方向相对于2DEG平面是任意的，而且在金属性磁条上施加了一直流电压．通过对真实的GaAs材料系统的数值计算，我们揭示了，这样的器件确实拥有一个相当的GMR效应，而且它的磁阻比率强烈地依赖于磁条上的应用电压.这样我们所考虑的纳米系统可以被用作一个GMR器件，其磁阻比率可通过改变磁条上的应用电压进行调节．

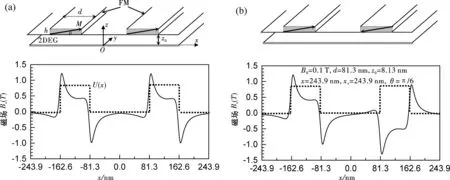
图1 GMR模型

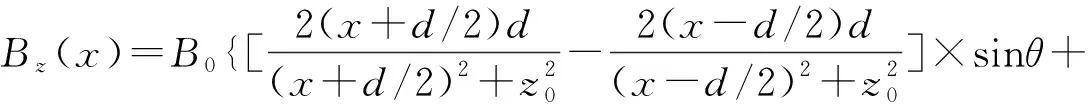
(1)

其中B0=Mh/d．当负电压加在金属磁条上时，在2DEG内就会诱发一个电垒(EB)U(x)，如图1中的点线所示，其可近似成方形电势垒[6]．在这样调制的2DEG系统中运动的电子可以通过单粒子Hamiltonian来描述：

(2)

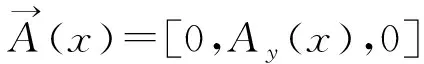
(3)

由于系统沿着方向平移协变，总的电子波函数可写为Φ(x,y)=exp(ikyy)ψ(x)，其中ky是电子y方向的波矢分量．因此，波函数ψ(x)满足下面的简化的一维Schrödinger方程：

(4)

我们引入有效势：

Ueff(x,ky)=[ħky+eAy(x)]2/(2m*)+m*g*σzBz(x)/(4m)-U(x).

显然，该系统的有效势不仅强烈地依赖于磁构型Bz(x)和纵向波矢ky，而且依赖于EB高度U(x)．有效势的波矢依赖性表明电子在系统中的运动本质上是一个二维过程，而从其对磁构型的依赖性可知：图1所示的器件从P构型转到AP构型时，有效势Ueff发生巨大变化，从而导致系统具有GMR效应．

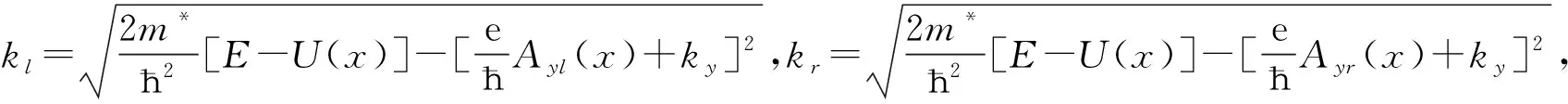
T(E,ky,U)=|τ|2.

(5)

从而，我们可以根据熟悉的Landauer-Buttiker公式[11]，计算零温时的弹道电导：

(6)

这里，φ是相对于x方向电子的入射角．电导以G0=2e2m*vFLy/h2为单位，其中vF是Fermi速度，Ly是系统的纵向长度．

对于一个GMR器件，它的磁阻比率通常有两种定义[5-7]，即MRR=(GP-GAP)/GAP或MRR=(GP-GAP)/GP和MMR=(GP-GAP)/(GP+GAP)，其中GP和GAP分别是P构型和AP构型的电导．显然，按照不同的定义计算的磁阻比率对某些情况而言是不同的．在这篇文章中，如同文献[6,7]我们采用定义MRR=(GP-GAP)/GAP研究GMR效应．注意到，虽然δ函数型磁场Bz(x)是局部无限的，但是极化项g*m*Bz(x)对GMR的影响趋向于整个空间．不过，Zeeman耦合项对GMR的影响依赖于量g*Bm*/4m，其值对于B=5和GaAs材料(m*=0.067m、g*=0.44)为0.036 9，与有效势Ueff中的其他项相比Zeeman项的绝对值很小，所以在决定属于特性时与自旋有关的项起到很小的作用[7]，因而对GaAs系统可以忽略[8]．

下面取GaAs作为2DEG的材料，并假定结构参数B0=0.1 T，d=81.3 nm，z0=8.13 nm，θ=π/6和x±=243.9 nm．图2给出P构型(虚线)和AP构型(点线)的透射系数与入射能量E的关系，其中电子波矢ky=8.6 μm-1，3个EB高度(a)U=0 meV，(b)U=0.34 meV和(c)U=0.68 meV．显然，电子通过P构型和AP构型的透射系数存在明显差异．对于P构型，我们可以清楚地看到在低能区有几个理想的共振峰，其原因是对于所考虑的波矢ky有效势Ueff具有对称的多垒结构[12]，其中电子的运动是共振地通过这些垒．但是，当系统从P构型转成AP构型时，我们可以看出电子的透射被镇压了，这是因为对于AP构型有效势Ueff为不对称的多垒或阱，使电子透射不完备．还可以看出，电垒U改变透射的起始位置和透射峰或谷的位置，即当增加电垒高度时透射曲线移向高能区并被改变．这样，P构型和AP构型电子透射系数的差异对电垒高度U的依赖性，起源于电垒高度变化U引起的有效势Ueff改变的结果．

上面显示的依赖于构型和电垒的透射特点，应该要反映在可测量电导G上来，其通过电子透射系数过入射角度的积分得到，如方程(6)所示．我们的计算结果证实了电导GP和GAP对构型和电垒的依赖性．在图3，我们作出了电导GP(虚线)和GAP(点线)随Fermi能EF变化的曲线，图中EB高度取为(a)U=0 meV，(b)U=0.34 meV，(c)U=0.68 meV，而结构参数与图2相同并且电导以G0为单位．由于与P构型透射系数TP对比AP构型的透射系数TAP大大地减少，电导GAP的巨大镇压明显可见．事实上，正是对AP构型电导的大的镇压，导致我们所考虑的器件具有明显的GMR效应[6]．此外，我们也可以看到，随着EB变高，P和AP构型的电导曲线都移向高Fermi能方向，而且它们之间的差异明显被改变．该系统的GMR效应对EB高度显示了一个明显的依赖性．

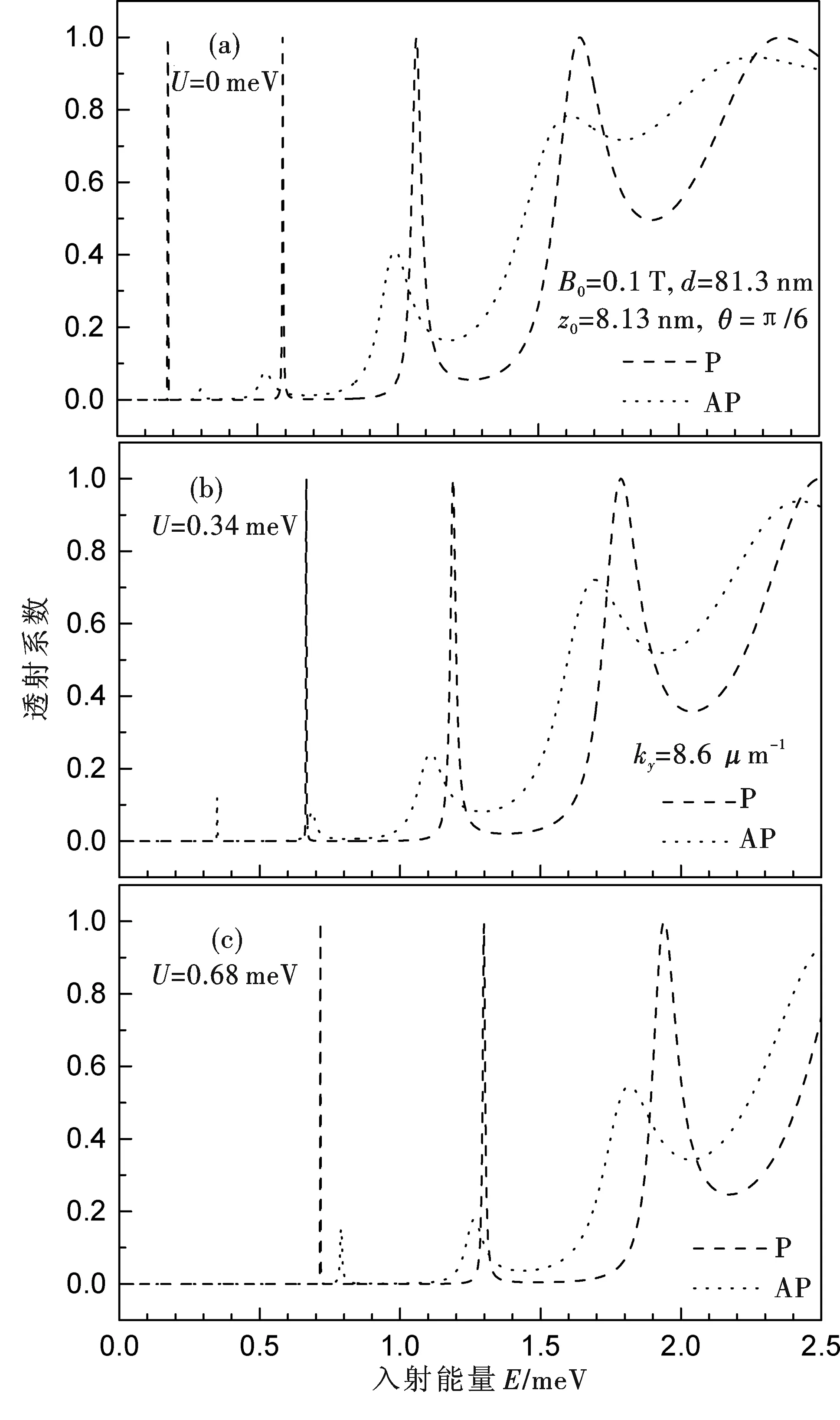
图2 电子通过P构型和AP构型的透射系数

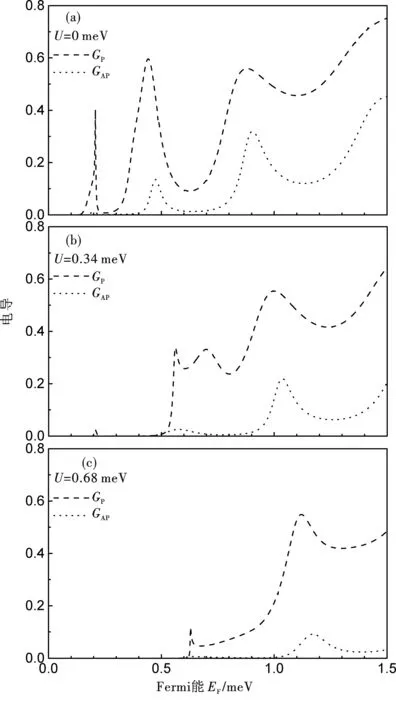
图3 P构型和AP构型的电导

为了有一个更好的观察，我们考虑系统的磁阻比率MRR(其定义为MRR=(GP-GAP)/GAP)随Fermi能EF变化的曲线，其结构参数与图3一样，电垒EB高度取为U=0，0.34，0.68 meV．一个相当明显的GMR效应清楚可见，特别是在低能区域磁阻比率MRR高达104%数量级．当Fermi能改变时，GMR效应随Fermi能展现了明显的振荡．我们也可明显看到，GMR效应强烈依赖于电垒高度．随着增加电垒高度，磁阻比率MRR移向高Fermi能区域，并且大大地被改变．

从实际应用的观点，对GMR器件其磁阻比率可控是人们所渴望的．现在，通过改变电路EB高度(即施加在系统中金属性磁条上的直流电压)，来研究所考虑系统的GMR效应的可调性．对于3个固定的Fermi能EF=0.51，1.02，1.53 meV，作为电垒EB高度U(x)我们计算了系统的磁阻比率MRR．结果发现磁阻比率MRR随着改变电垒EB高度大大地改变了．当电垒EB高度变高时，对某个固定的Fermi能磁阻比率的值大大被改变．另外，随着增加Fermi能EF，磁阻比率MRR曲线移向右方，而且它的大小明显改变，但是，其随U(x)变化的范围延伸了．这些特点起源于系统有效势Ueff对电垒EB高度U(x)的依赖性．因为EB高度由施加在系统中金属性磁条上的直流电压产生，所以人们可以通过改变这个应用电压来调控系统的磁阻比率，因而可导致一个电压可控的GMR器件．

总之，我们从理论上研究了一般的磁调节和电调节半导体纳米系统中的巨磁阻效应，实验上该系统可通过在常规半导体异质结(比如，GaAs/AlGaAs系统)表面上沉积2个平行的金属性磁条来实现，其中磁条上施加了直流电压．我们的计算显示，由于P构型和AP构型之间存在明显的隧穿差异，特别是AP构型透射的镇压，这样的纳米系统显示了一个明显的GMR效应．我们也揭示了，其磁阻比率受系统中磁条上施加的电压影响，从而可导致一个电压可调的GMR器件．

参考文献：

[1] BAIBICH M N, BROTO J M, FERT A,etal. Giant magnetoresistance of (001)Fe/(001)Cr magnetic superlattice[J]. Phys Rev Lett, 1988, 61(21):2 472-2 475.

[2] SCHEP K M, KELLY P J, BAUER G E W. Ballistic transport and electronic structure[J]. Phys Rev B, 1998, 57(15):8 907-8 926.

[3] NOGARET A, CARLTON S, GALLAGHER B L,etal. Observation of giant magnetoresistance due to open orbits in hybrid semiconductor/ferromagnet devices[J]. Phys Rev B, 1997, 55(24): 16 037-16 040.

[4] OVEREND N, NOGARET A, GALLAGHER B L,etal. Temperature dependence of large positive magnetoresistance in hybrid ferromagnetic/semiconductor devices[J]. Appl Phys Lett, 1998, 72(7):1 724-1 728.

[5] EDMONDS K W, GALLAGHER B L, MAIN P C,etal. Magnetoresistance oscillations due to internal Landau band structure of a two-dimensional electron system in a periodic magnetic field[J]. Phys Rev B, 2001, 64(4):041303.

[6] ZHAI F, GUO Y, GU B L. Giant magnetoresistance effect in a magnetic-electric barrier structure[J]. Phys Rev B, 2002, 66(12):0125305.

[7] YANG X D, WANG R Z, GUO Y,etal. Giant magnetoresistance effect of two-dimensional electron gas systems in a periodically modulated magnetic field[J]. Phys Rev B, 2004, 70(11):0115303.

[8] PAPP G, PEETERS F M. J Phys: Condens[J]. Matter, 2004, (16):8 275-8 279.

[9] VANCURA T, IHN T, BRODERICK S,etal. Electron transport in a two-dimensional electron gas with magnetic barriers[J]. Phys Rev B, 2000, 62(8):5 074-5 077.

[10] MATULIS A, PEETERS F M, VASILOPOULUS P. Wave-vector-dependent tunneling through magnetic barriers[J]. Phys Rev Lett, 1994, 72(6):1 518-1 526.

[11] BUTTIKER M. Four-teminal phase-coherent conductance[J]. Phys Rev Lett, 1986, 57(14):1 761-1 766.

[12] YOU J Q, ZHANG L D, GHOSH P K. Electronic transport in nanostructures consisting of magnetic barriers[J]. Phys Rev B,1995, 52(24):17 243-17 247.