随机环境下生产和运输成本问题的线性规划方法
2010-11-26阳彩霞
万 中,阳彩霞,江 卫
(中南大学数学科学与计算技术学院, 中国 长沙 410083)
一个复杂的决策系统通常具有多维性、多样性、多功能性和多准则性,并有时带有随机参数.含有随机参数的数学规划称为随机规划(SP).随机规划为解决带有随机参数的优化问题提供了有力的工具.对随机优化问题中所出现的随机参数,根据不同的管理目的和技术要求,所采用的处理方法也不尽相同[1-2].
目前处理随机规划问题最常用的重要方法有2种:第1种是期望值(EM)方法[3],该方法通过取随机变量的数学期望,把随机规划问题转化为确定性数学规划问题.第2种方法是机会约束规划方法(简称CCPM),该方法由Charnes和Cooper率先提出,它考虑到了在不利情况发生时所作出的决策可能不满足约束条件,因此采取一种原则:要求所作的决策在一定置信水平内满足约束条件[4].
CCPM方法自60年代提出以来,发展迅速.近年来的相关研究成果可参阅文献[5]~[11],以及其后所列的参考文献.他们利用CCPM成功地解决了来自不同领域(如工业过程和经济管理)中的许多问题,诸如水库管理,电力生产,主板生产,化学工程,电信及财经等方面的实际问题.
本文作者的目的是研究典型的生产和运输成本问题.针对该类问题,最近文献[12]在建立其优化模型的基础上,通过引进0-1整数变量,提出了分段线性逼近法求解产品成本为凹函数的大型产品运输问题.其不足在于所建立的模型视厂家的生产能力和商家的需求量为确定常数.在文献[11]中,万中等人利用机会约束规划方法研究了生产厂家的生产能力,商家的需求量和单位运输成本等因素都是随机变量情况下的多产品生产和运输问题.该论文中建立的模型和求解方法虽然具有一般性,但得到的原问题的确定型等价式却是非线性模型.针对此类问题求解的复杂性,万中等人在文献[10]中还进一步研究了线性逼近方法.
与已有工作不同,本文考虑生产厂家的生产能力和商家的需求量是随机变量情况下的多产品生产和运输问题.我们将证实与原问题对应的确定型等价式是一个含0-1变量的线性规划问题,不仅比文献[11]中建立的模型要容易求解,而且保证了文献[12]中的设计方法可以应用于随机环境.
1 问题描述和模型
典型的生产和运输成本问题可描述如下:假设某种物资由A、B、C……若干生产商或供应商生产或供应,该种物资需要运送给1、2、3……等销售地或需求点.我们的目标是在保证供需平衡的条件下如何确定最佳的生产和运输方案.用数学方式表述就是,设m是生产厂家个数,n是销售点个数,ai,i=1,2,…,m,是第i个厂家的生产能力,bj,j=1,2,…,n,是第j个商家的需求量,wi是第i个厂家需要生产的产量,gi(wi)为第i个厂家生产wi所需的生产成本,xij是厂家i给销售点j的送货量,cij为厂家i到销售点j的单位运输成本.以wi,xij为决策变量,确定最佳生产和运输方案问题可写成如下优化模型:

xij≥0,i=1,2,…,m,j=1,2, …,n,
(1)
其中运输成本由目标函数中的第1个和式(线性部分)确定,生产成本由目标函数中的第2个和式(可分离线性或非线性部分)确定.当且仅当厂家所能生产的产品量大于商家的需求量时,问题(1)的可行解存在.

一般地,当假设模型(1)中的所有参数为确定常数时,问题(1)是一个线性约束的非线性规划问题.通过引入0-1变量,文献[12]在假设生产成本函数为凹函数的条件下,利用分段线性逼近法将原问题归结为一系列的带0-1变量的线性规划问题求解.但实际中,ai和bj,i=1,2,…,m,j=1,2,…,n,常为随机变量.这时,问题(1)一般不再是线性约束的非线性规划问题.因此,文献[12]提出的线性化方法不再合适.不过,即使是在随机情况下,当采取独立机会约束方法处理原问题时,(1)仍是线性约束的非线性规划问题,从而保证[12]中的方法能够推广到求解随机情况下的生产和运输计划问题.
假设ai和bj均为服从正态分布的随机变量,
则约束条件
(2)
和
(3)
可分别松弛为
(4)
和
(5)
其中αi,βj∈[0,1]叫做约束满足的置信水平.
若αi=βj=1,则条件(4)即为条件(2),条件(5)即为条件(3).只是ai和bj为随机变量时,其解集的测度可能为零.
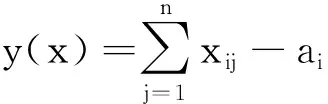
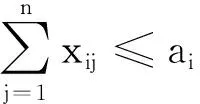
而
是服从标准正态分布N(0,1)的随机变量,其概率分布函数形式为
所以,机会约束(4)等价于
(6)
同理,机会约束(5)可写成
(7)
通常把(6)和(7)分别称为(4)和(5)的确定型等价类.显然,约束条件(6)和(7)仍是线性约束.
下面我们说明在假设gi为凹函数时,如何线性化目标函数.
将区间[0,ai],i=1,2,…,s,分割成k个相等的子区间,0≡zi0 (8) 其中 λil≥0,l=0,1,…,k, λi0≤yi0, λil≤yil-1+yil,l=1,2,…,k, yil∈{0,1},l=0,1,…,k. 这样,原问题就转化为如下含0-1变量的线性规划问题: xij≥0,i=1,2,…,m,j=1,2,…,n, λi0≤yi0,i=1,2,…,s, λil≤yil-1+yil,,i=1,2,…,s,l=1,2,…,k, λil≥0,i=1,2,…,s,l=1,2,…,k, yil∈{0,1},i=1,2,…,s,l=1,2,…,k. (9) 下面把本文建立的模型和求解方法应用于一个实际问题.假设有4个工厂:工厂1,工厂2,工厂3,工厂4;3个商场:商场A,商场B,商场C.把工厂与商场之间的物理距离看成单位运输成本,各个工厂与商场之间的物理距离由如下矩阵给定: minf(x,w)=(12x11+21x12+21x13)+(13x21+20x22+23x23)+(15x31+17x32+27x33)+ (17x41+19x42+31x43)+250[(x11+x12+x13)0.6+(x21+x22+x23)0.6+(x31+x32+x33)0.6+ (x41+x42+x43)0.6] s.t.x11+x12+x13≤200-Φ-1(0.95)×10, x21+x22+x23≤300-Φ-1(0.95)×10, x31+x32+x33≤400-Φ-1(0.95)×10, x41+x42+x43≤200-Φ-1(0.95)×10, x11+x21+x31+x41≥100+Φ-1(0.95)×10, x12+x22+x32+x42≥300+Φ-1(0.95)×10, x13+x23+x33+x43≥400+Φ-1(0.95)×10, xij≥0,i=1,2,…,4;j=1,2,…,3. (10) 该模型的约束条件都是线性的,目标函数是线性函数与幂函数的和.因此可以利用上一节提出的转化方法,把此类非线性优化问题直接转化为含0-1变量的线性规划问题.我们在Lingo 7.0 平台上得到原问题最优解是 w*=(0.000 0,25.325 0,158.225 0)T,f*=4 713.4. 从上述实例的求解过程可以看出,虽然本文建立的多产品生产和运输问题的数学模型不如文献[10]中的模型具有一般性,但利用本文提出的方法处理随机环境下多产品生产和运输问题,比[10]中的线性逼近方法效率更高. 本文利用机会约束规划方法,把随机环境下的产品生产和运输成本问题转化为含0-1变量的线性规划问题来求解.数值算例表明了本文所建立的模型和求解方法的有效性. 参考文献: [1]BIRGEJR,LOUVEAUXFV,Introductiontostochasticprogramming[M].NewYork:Springer, 1997. [2] 刘宝碇,赵瑞清.随机规划与模糊规划[M].北京:清华大学出版社,2001. [3]DANTZIGGB.Linerprogrammingunderuncertainty[J].ManagementScience, 2004, 50(12):1 764-1 769. [4]CHARNESA,COOPERWW.Chance-constrainedprogramming[J].ManagementScience, 1962,6(1):73-79. [5]FREDRICKS,HILLIERFS.Chance-constrainedprogrammingwith0-1orboundedcontinuousdecisionvariables[J].ManagementScience, 1967,11(1):34-57. [6]OLSONDL,SWENSETHSR.Alinearapproximationforchanceconstrainedprogramming[J].JournaloftheOperationalResearchSociety, 1987, 38(3):261-267. [7]PANNEVD,POPPW.Minimumcostcattlefeedunderprobabilisticproteinconstraints[J].ManagementScience, 1963,9(3):405-430. [8]SEPPALAY.Constructingsetsofuniformlytighterlinearapproximationsforachance-constraint[J].ManagementScience, 1971, 17(11):736-749. [9]YAHIAZM,AHMADD.Alinearapproximationmethodforsolvingaspecialclassofthechancecongstrainedprogrammingproblem[J].EuropeanJournalofOperationalResearch, 1995, 80(1):213-225. [10] 万 中,江 卫,阳彩霞,等.一类求解带随机成本的生产运输问题的线性逼近方法[J].工程数学学报,2010,27(3):381-388. [11] 万 中,阳彩霞,江 卫,等.生产运输成本问题的随机优化模型及新的求解途径[J].模糊系统与数学,2009,23(3):145-151. [12]HIROSHIK,TAKAAKIE.Computationalstudiesonlargescaleconcavecosttransportationproblems[J].PacificJournalofOptimization, 2006, 2(2):327-339 [13]WEINTRAUBA,VERAJ.Acuttingplaneapproachforchanceconstrainedlinearprograms[J].OperationResearch, 1991, 39(5):770-776.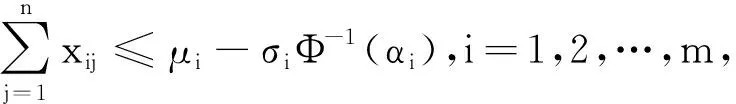
2 数值算例
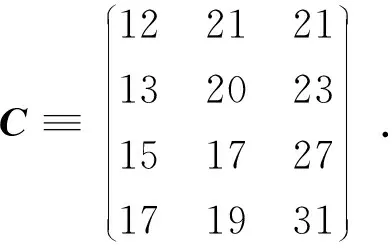
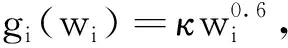
3 结论
