Nonlocal Kuramoto-Sivashinsky方程渐近吸引子的构造
2010-11-26罗宏
罗 宏
(四川师范大学数学与软件科学学院,中国 成都 610066)
本文作者研究了具有周期边界条件的Nonlocal Kuramoto-Sivashinsky方程:
(1)
uxj(x,t) =uxj(x+l,t),j=1,2,3,4,t∈R+,
(2)
u(x,0) =u0(x),u0(x) =u0(x+l),
(3)
其中, 0<γ<1,α>0,
(4)
它描述了混合气体燃烧过程中火焰是如何随时间演变的, 所以讨论方程(1)~(4)的解的性态具有重要意义. 文[1~2]研究了这类方程解的先验估计以及整体吸引子和惯性集的存在性, 文[3]讨论了该方程数值解法.
在无穷维动力系统研究中, 方程解的长时间性态是一个重要问题, 备受关注. 通常,方程解的长时间性态由具有有限维特征的全局吸引子所表现[4-5]. 然而, 对于一般情形, 研究全局吸引子是相当困难的. 因而, 人们想到借助其他的东西来代替全局吸引子. 1985年和1987年, G. Foias等[6-7]先后提出了惯性流形和近似惯性流形, 但是它们在研究中存在很大的局限性.文献[8]提出了有限维渐近吸引子的概念, 构造了Kuramoto-Sivashinsky方程的渐近吸引子,证明了所得的系统与原系统等价.
对一个发展系统
ut+Au=f(u)
(5)
来说, 记其相空间为H, 解算子半群为{S(t),t≥0}, 吸收集为. 假设对任意u0∈, 存在N维子空间中的近似解序列{uk(t)},k≥1,满足
‖uk(t)-S(t)u0‖H→0,k→+∞,t≥t*().
本文在文献[1~3, 8~10]的基础上讨论了Nonlocal Kuramoto-Sivashinsky方程周期边值问题(1)~(4)解的长时间性态,构造了方程的渐近吸引子.
为了方便讨论, 设v=ux, 则方程(1)~(4)可以化为下列形式
vt=-vxxxx-vxx-vvx+γJ(v)-αxvx-2αv,(x,t)∈R×R+,
(6)
vxj(x,t)=vxj(x+l,t),j=0,1,2,3,t∈R+,
(7)
v(x,0)=v0(x),v0(x)=v0(x+l),
(8)
其中
(9)
1 预备知识与解序列的构造

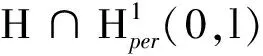


pt+pxxxx+pxx+PN(vvx)-γJ(p)+αxpx+2αp=0,
qt+qxxxx+qxx+QN(vvx)-γJ(q)+αxqx+2αq=0.
(10)
对任意初值v0(x)∈,按如下方式构造渐近解序列
(11)
(12)
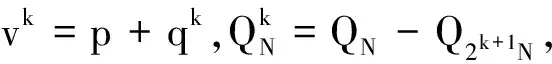
2 逼近性证明
下面将考虑渐近解序列vk(x,t)对真实解v(x,t)的逼近性.首先证明,对任意v0∈,上述所得的解序列不会远离吸收集.
定理1设v(t)是对应于初值v0∈的方程(6)~(9)的解,qk(k=0,1,2,…)按(11),(12)给出,则存在自然数N0和t1(),使得当N≥N0时,有
(13)
证由吸收集的正不变性,v0∈可以得出v(t)∈,t≥0,从而,‖p‖≤ρ0,‖px‖≤ρ1.为了证明(13)式,只须证明
(14)
即可.下面用数学归纳法证明(14)成立.
在(11)两边乘以q0,在[0,l]上积分,得
故

从而
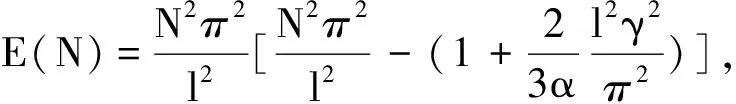
即
在(0,t)上积分,得

‖q0‖≤ρ0,t≥t11.
(15)

(16)
(15),(16)证明了(14)在k=0时成立.
现假设(14)对k-1成立,在(12)两边乘以qk,在[0,l]上积分,得
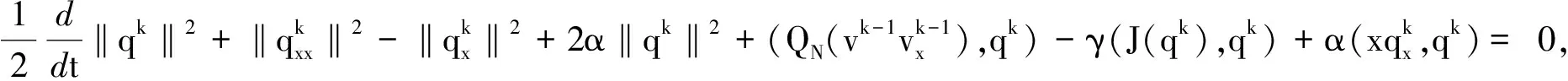
故,
从而
则有
即
在(0,t)上积分,得
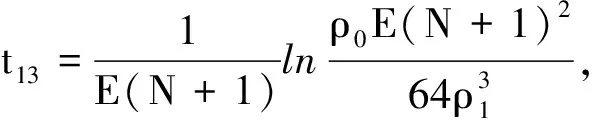
(17)
则
‖qk‖≤ρ0,t≥t13.
(18)
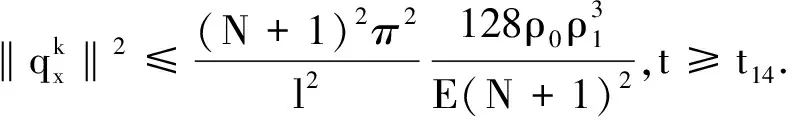
(19)
则
(20)
由(18)和(20)式可知(14)式对k成立.由数学归纳法原理知,当N0取满足(17),(19)的最小自然数,t1()=max{t11,t12,t13,t14},(14)式对一切自然数k成立,则该定理得证.
下面证明qk收敛于q.
定理2设v(t)是对应于初值v0∈的方程(6)~(9)的解,qk(k=0,1,2,…)按式(11),(12)给出,则存在自然数N1和t2(),使得当N≥N1时,有),其中,N1为满足
(21)
的最小自然数.
证记ωk=qk-q,k=1,2,…,由(10)和(12)得
所以
故

从而
所以
(22)
在(22)中,令k=1,则有t21>0,使得
(23)
在(22)中使用数学归纳法易得,存在t2k>0,k=1,2,…,使得
(24)
由(23),(24)可知,取N1为满足
的最小自然数.则该定理得证.
上述两定理证明了渐近解序列对真解的逼近性,而且渐近吸引子的维数,就是渐近解序列的维数,为满足(17),(19),(21)的最小自然数,即,
参考文献:
[1] HILHORST D, PELETIER L A, ROTARIU A I. Global attractor and inertial sets for a Nonlocal Kuramoto-Sivashinsky equation [J]. Disc Cont Dyna Sys, 2004, 10(1,2): 557-580.
[2] 童筱青, 向新民. 非局部Kuramoto-Sivashinsky方程整体吸引子的维数估计[J]. 应用数学学报, 2009, 32(5): 881-893.
[3] 童筱青, 周 婷, 向新民. 非局部Kuramoto-Sivashinsky方程谱逼近的大时间性态[J]. 高等学校计算数学学报, 2005, 27: 259-264.
[4] TEMAM R. Infinite-dimensional dynamical systems in mechanics and physics[M].2nd ed. Berlin:Springer-Verlag, 1997.
[5] 郭柏灵. 无穷维动力系统[M]. 北京: 国防工业出版社, 2000.
[6] FOIAS G, SELL G R, TEMAM R. Varites inertilles des equations differentielles dissipatives[J]. C R Acad Sci Paris Ser I Math, 1985, 301: 139-142.
[7] FOIAS G, MANLEY O, TEMAN R. Sur linteraction des petits et grands tourbillon’s dans les ecoulements turbulents[J]. C R Acad Sci Paris Ser I Math, 1987, 305: 497-500.
[8] 王冠香, 刘曾荣. Kuramoto-Sivashinsky方程的渐近吸引子[J]. 应用数学学报, 2000,23(3): 329-336.
[9] 罗 宏, 蒲志林, 马丽蓉. 耗散KDV型方程的渐近吸引子[J]. 四川大学学报:自然科学版,2009,46(6):1 709-1 713.
[10] 何素芳,朱朝生.推广的B-BBM方程的渐近吸引子[J]. 四川师范大学学报:自然科学版,2007,30(1):49-52.
