基于Richards变换与Kuroda规则的微带低通滤波器的设计仿真

王汉江,吴姣,杨维明,陈军,杨安胜

(湖北大学 物理学与电子技术学院,湖北 武汉 430062)

在无线通信系统中,高性能的低通滤波器起着非常重要的作用,它常被用来抑制系统的谐波输出.微带线低通滤波电路是一种结构简洁的电路,非常便于电路的设计和实现.当频率较低时,射频滤波器的设计可以采用分立元件来实现;频率增大意味着波长减小,当频率超过500 MHz时,工作波长与滤波器的物理尺寸相近,电阻、电容以及电感等元件的电响应将偏离它们的理想频率特性,产生损耗且电路性能也随之恶化,此时必须考虑分布参数效应.在设计微带线滤波器的时候应将集总参数元件变换成分布参数元件.本文中首先简要介绍Richards变换、单位元件概念以及Kuroda规则,然后以一个5阶契比雪夫低通滤波器为例,分析讨论基于Angilent ADS2005软件仿真平台的设计与优化方法.

1 Richards变换与Kuroda规则

1.1 Richards变换原理为了将集总参数元件变换成分布参数元件,Richards提出了一种独特的变换,该变换可将一段开路(短路)传输线等效于分布的电感(电容)元件.由传输线理论知,一段特性阻抗为Z0的终端短路传输线具有纯电抗性输入阻抗： Zin∶Zin=jZ0tan(βl)=jZ0tan(θ)

(1)

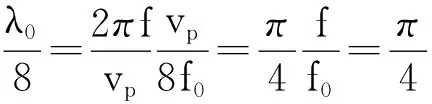
(2)

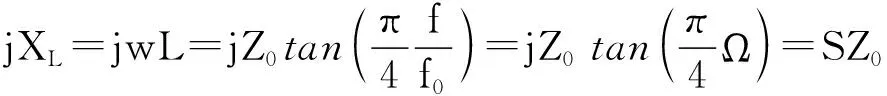
(3)

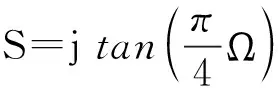
(4)

利用Richards变换可以用特性阻抗Z0=L的一段短路传输线替代集总参数电感,也可以用特性阻抗Z0=1/C的一段开路传输线替代集总参数电容.由于传输线的长度选为λ0/8(也可选为λ0/4),变换过程将集总参数元件在[0,∞)区间的频率响应映射到[0,4f0)区间,以及正切函数的周期性,使频率响应被限制在[0,2f0)区间.

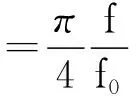
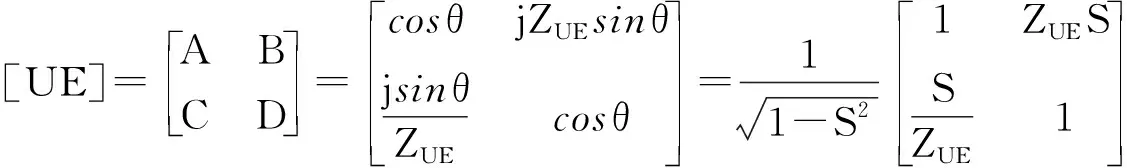
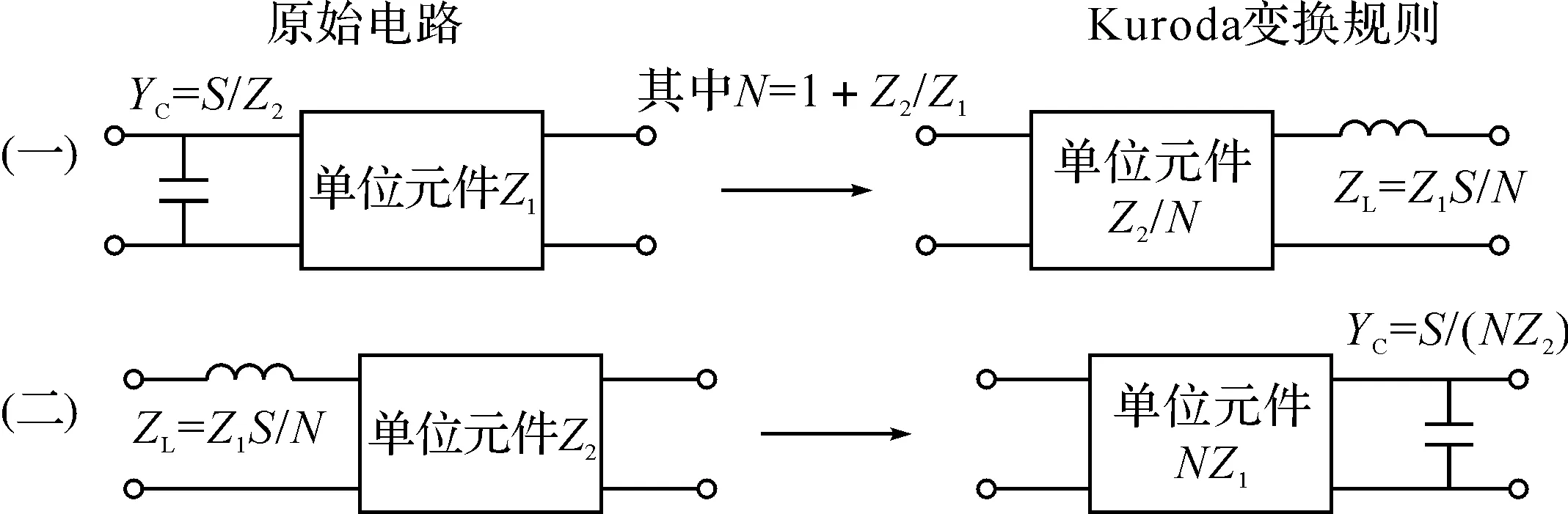
图1 Kuroda规则

1.2 Kuroda规则为了方便各种传输线结构之间的相互变换,使工程上难于实现的滤波器形式变换成容易实现的形式,Kuroda提出了四个电路变换规则,由于本文中只用了其中两个,故列出其中两个如图1.

现将第一栏中左右两式证明如下:

我们已经知道,整个电路的ABCD参量矩阵等于各个单元电路ABCD参量矩阵的乘积,对于左边原始电路而言,整个网络的ABCD参量矩阵为:

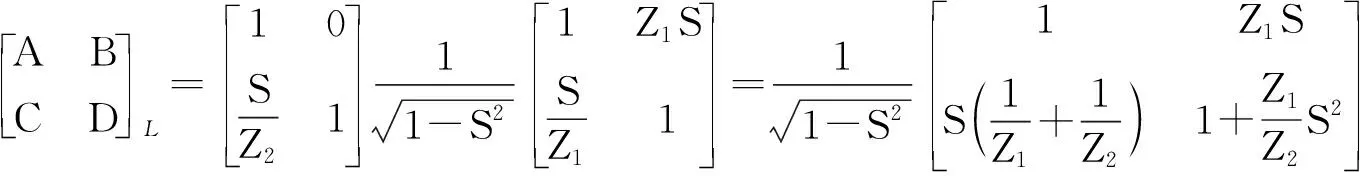
对于右边变换后的电路而言,整个网络的ABCD参量矩阵为:

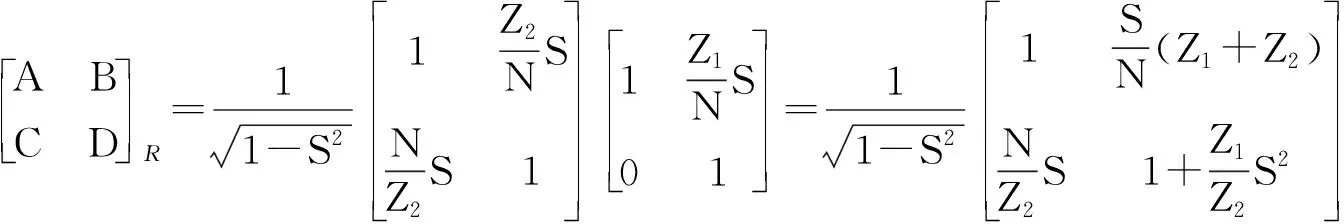
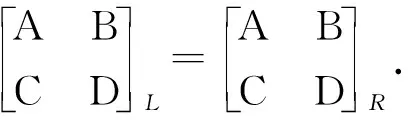
用同样的方法可以证明第二栏中左右两个电路的ABCD参量矩阵也是相等的[2].

2 微带线滤波器设计实例

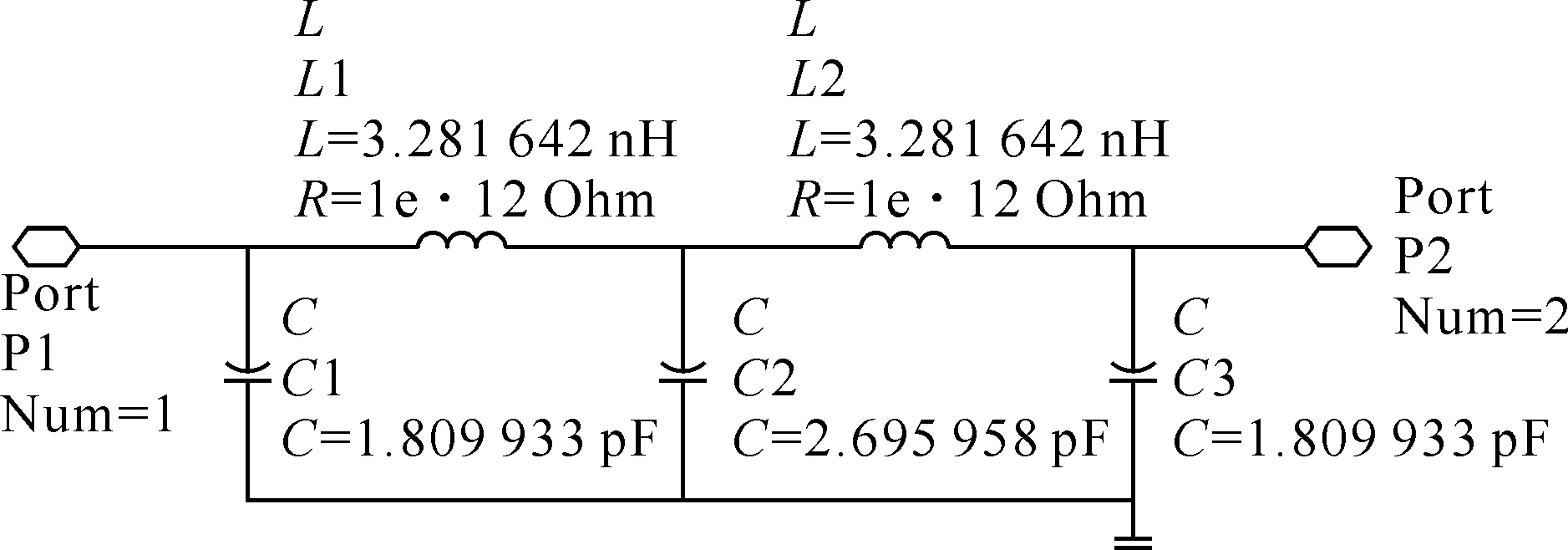
图2 低通滤波电路

截止频率为f0=3 GHz,通带内波纹为0.5 dB,在两倍截止频率处具有不小于40 dB的带外衰减,输入输出阻抗为50Ω.线路板厚度为H=1 mm,介质的相对介电常数为εr=2.7.首先设计集总参数的低通滤波电路.根据设计要求,选用0.5 dB等波纹契比雪夫滤波电路.由ADS软件模拟出5阶的滤波电路在截止频率Fs=6 GHz处,带外衰减大于40 dB.集总参数的电路结构如图2所示.

由前面讨论的Richards变换知,可以用特性阻抗z0=L的一段短路传输线替代集总参数电感,也可以用特性阻抗z0=1/C的一段开路传输线替代集总参数电容.该变换可以调用ADS软件中提供的宏函数实现,从而避免了冗长繁杂的计算过程,这也体现了仿真软件的高效便捷,变换后的电路如图3所示[3].

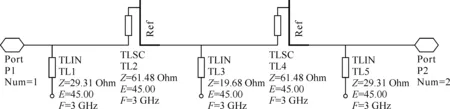
图3 经过Richards变换后的电

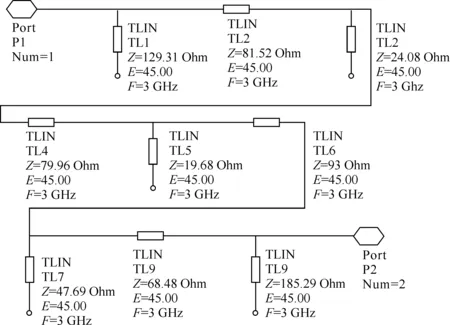
图4 经过Kuroda变换后的电路

在工程实际中,实现等效的串联感抗时,采用短路传输线段比采用并联开路传输线段更困难,所以此处利用Kuroda规则将串联的短路传输线段转换为并联的开路传输线段.为了匹配,转换前需插入单位元件(UE).转换后的电路图如图4所示.并联的5段开路传输线是该滤波器的5个单元,串联的4段传输线是插入的四个单位元件(UE)经过转化后的传输线段.

利用ADS软件将传输线段转换为厚度为H=1 mm,介质的相对介电常数为εr=2.7的微带线结构,为了减小各传输线接头处的不连续性而加入T形接头,使仿真达到指标.修改后电路如图5所示.

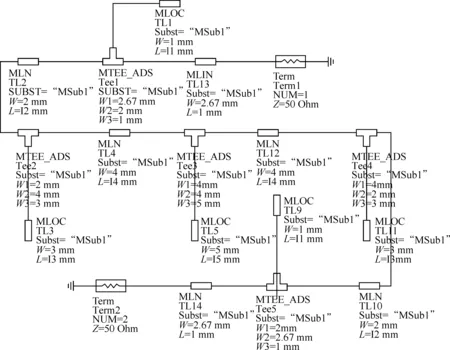
图5 转换为微带线结构的电

仿真结果如图6所示,由图可以看出该滤波器的截止频率大于3 GHz,通带内的反射损耗在-40 dB以下,在通带外的6 GHz处的衰减达到74 dB以上,达到了性能指标要求.该电路图的版图及其仿真结果如图7所示.

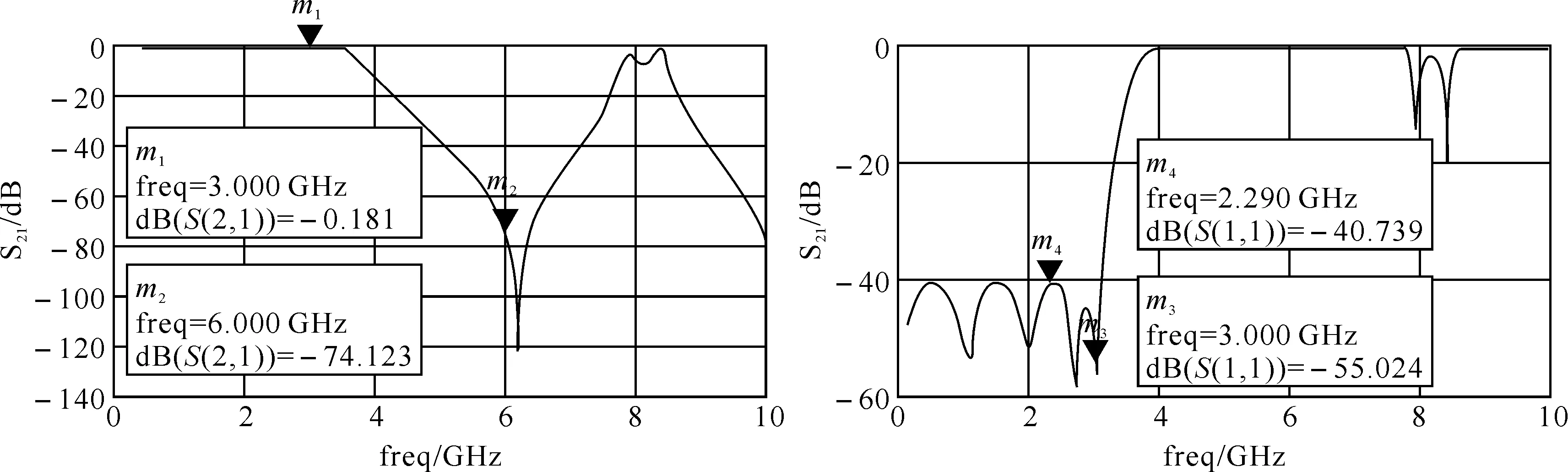
图6 电原理图仿真结果

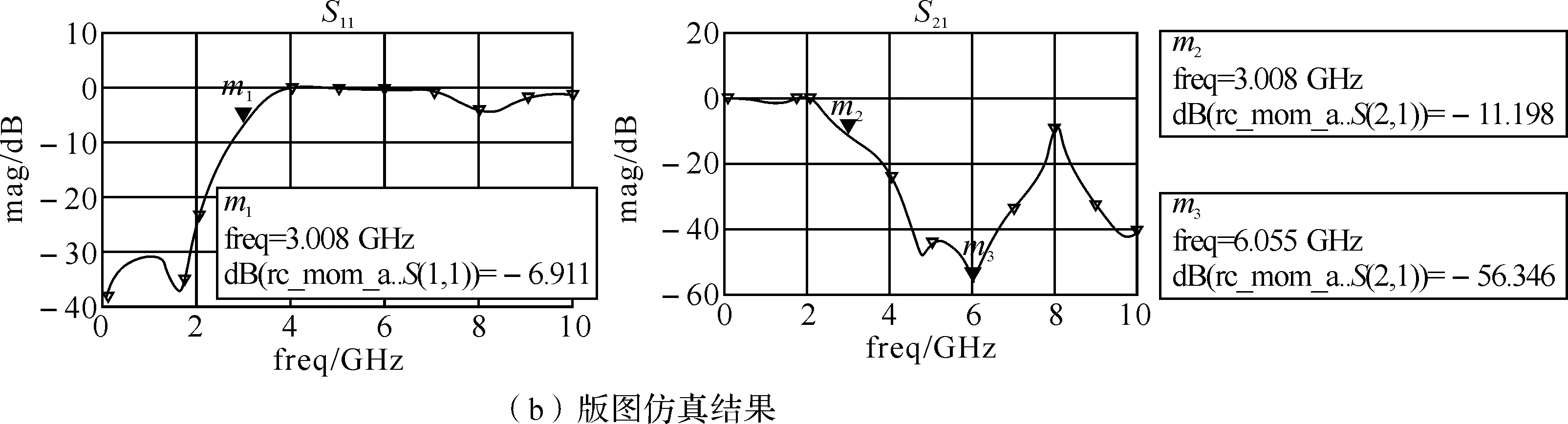
图7 低通滤波器版图及其仿真结果

从版图仿真结果可以看出通带内反射较大,能量没有得到有效传输.采用基于分形理论的滤波器设计技术[4],将版图做了多次尝试与修改,最终版图结构及其仿真结果如图8所示:

(a)优化后的低通滤波器版图

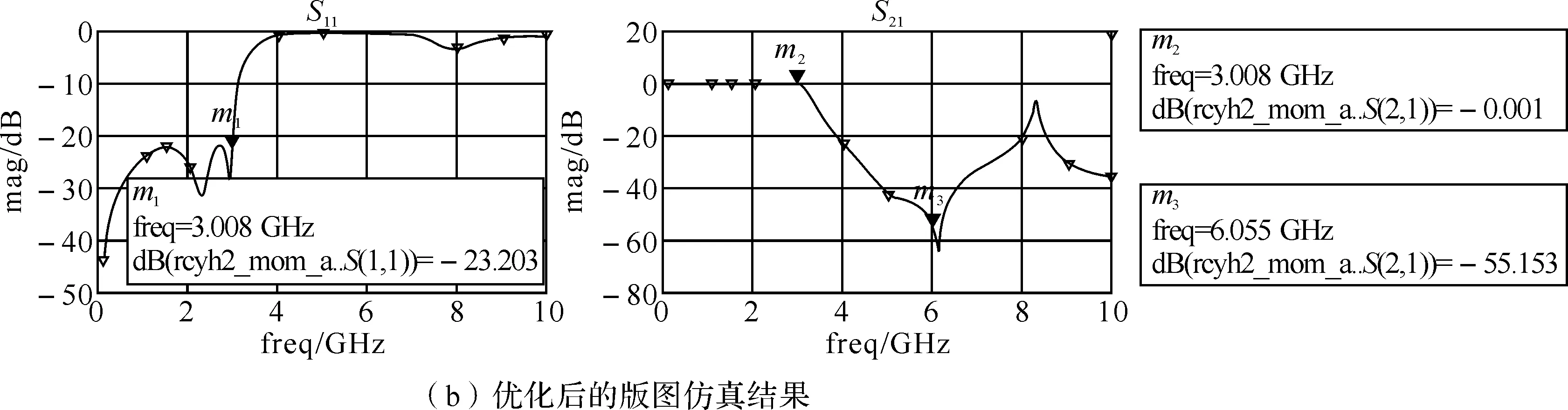
图8 优化后低通滤波器版图及其仿真结果

可以看出,通带内反射损耗明显改善,正向传输带宽也明显展宽,版图仿真结果也达到了性能指标.这种滤波电路具有结构紧凑、便于设计和尺寸小的优点.然而它要求传输线的长度远小于工作波长,随着输入射频信号频率的升高,如频率达到6 GHz,将不再满足设计的条件.

3 结束语

采用基于Richards变换与Kuroda规则的微带滤波器的结构和设计方法,基于Angilent ADS2005软件仿真平台设计了一个5阶契比雪夫低通滤波器并对其进行了优化仿真,使得电路仿真与版图仿真结果都达到了性能指标要求.本文中还介绍了Richards变换、单位元件概念以及Kuroda规则,在实际操作过程中均是利用ADS软件提供的宏函数来设计完成的,从而避免了冗长繁杂的计算过程,大大加快了滤波器设计周期,这也体现了仿真软件的高效便捷.

参考文献：

[1] Reinhold Ludwing,Pavel Bretchko.射频电路设计:理论与应用[M].王子宇,张肇仪,徐承和,等,译.北京:电子工业出版社,2002.

[2] 李征帆,毛军发.微波与高速电路理论[M].上海:上海交通大学出版社,2001,8:115-127.

[3] 杨金伟.基于Richards变换与Kuroda规则的射频滤波器设计[J],台州学院学报,2006,28(3):41-46.

[4] 陈文灵,王光明,齐谊娜,等.基于分形理论的高低阻抗线低通滤波器[J].电波科学学报,2008,23(3):506-509.