基于LS-DYNA的汽车前纵梁碰撞性能仿真研究
2010-11-22黎权波
高 伟,黎权波
(湖北汽车工业学院 汽车工程系,湖北 十堰442002)
汽车发生正面碰撞时,主要是由车身前部“压溃区”的塑性变形来吸收碰撞动能,并且主要是端部底架结构的大变形来缓和冲击和吸收冲击动能,因此端部底架结构上的前纵梁的吸能特性和变形模式,将决定着车体在撞击时的响应。前纵梁既是吸收汽车前部纵向碰撞能量的主要结构,又是控制碰撞能量在汽车中的分布情况的主要装置。据研究,设计良好的汽车前纵梁在正碰时吸收的能量能达到总吸收能量的50%以上,是最重要的吸能元件[1]。所以加强对前纵梁的变形和吸能特性的研究是建立整个车身变形和吸能特性与乘员保护之间的相关性模型的基础[2]。
在不改变汽车车身结构及造型的情况下,通过改进汽车前纵梁结构,使其具有较好的碰撞性能,是保证汽车具有良好正面碰撞性能的重要手段和方法[3]。本文通过对长安微型车前纵梁进行正面碰撞仿真分析,研究其碰撞变形吸能特性,对该前纵梁的结构进行了优化设计,从而使前纵梁的碰撞特性得到了加强。
1 前纵梁碰撞仿真分析
应用有限元法进行仿真分析,几何模型的建立是重要内容,也是求解的基础。然后对模型进行网格划分、设置约束、载荷和边界条件,最后进行求解得出结果。
1.1 前纵梁几何模型的建立
参考“长安之星”微型车前纵梁吸能段的结构,截面宽度为100 mm×80 mm,长度为350 mm的薄壁直梁。前纵梁的三维模型是利用CATIA软件中的创成式曲面设计进行绘制。
1.2 单元的选择
有限元空间域的离散可以有很多不同的方法,这些方法对应着不同的有限单元类型,常用的单元类型有:壳单元、实体单元和梁单元等。汽车中的大部分部件都是由金属薄板冲压而成,因此,本文在仿真模拟中采用壳单元描述前纵梁的变形特性。
1.3 材料特性
汽车吸能结构的设计是车辆设计的重要环节,良好的吸能结构应该使碰撞动能尽量转化为变形能。金属结构在受到撞击时,会发生塑性变形并产生一定的压溃距离来达到吸收碰撞动能的作用[4]。故在本文中,前纵梁材料按照普通低碳钢真实应力—应变材料特性设置为24号分段线性材料MATL24,见图1,并考虑材料应变率效应,选用Krupkswsky硬化模型和Cowper-Symonds应变率模型,选择经验值 C 为 40,p 为 5[5]。 属性为 1.2 mm厚度的Shell单元,算法采用默认算法,剪切因子SHRF为5/6,即0.83333,沿厚度方向积分点NIP为 5, 密度为 7.85×10-6kg·mm-3,E 为 210 kN·mm-2,NU 为 0.3,SIGY 为 0.17 GPa(170 MPa)。
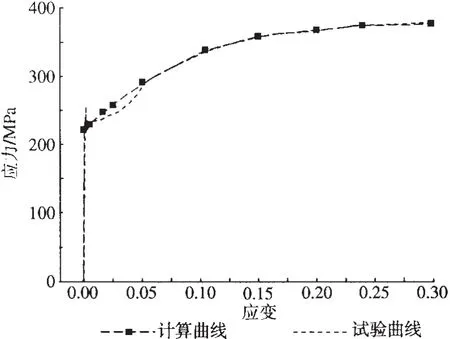
图1 模型采用的低碳钢材料特性
1.4 网格的划分
对于显式有限元,网格密度的选取是非常重要的,网格密度的不同对塌陷形式的描述的详略是不同的,计算时间的要求也不同。网格越密,计算时间越长,计算越精确,反之亦然。在单元网格密度控制上,尽管较小的单元尺寸对变形描述准确,但会大量增加计算时间,而较大的单元尺寸可能会引起较大的沙漏能,导致变形失真。双帽形截面薄壁梁的最佳单元尺寸可估计为
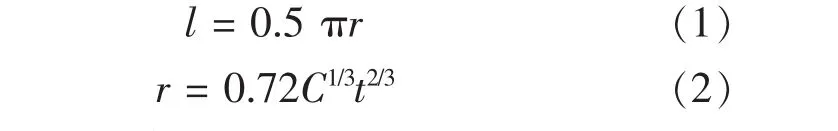
式中:C—— 截面宽;
t—— 板厚;
r—— 折叠半径。
综合考虑计算质量、时间后,本文前纵梁的单元尺寸取为5 mm。
2.4 焊点的布置
焊点质量、焊点分布方式影响着车身前纵梁各部件间的动力学关系,进而对前纵梁的变形模式、能量吸收及加速度变化等性能也将产生不可忽略的影响[6]。所以在前纵梁的设计时,必须考虑到这些有关焊点的参数。
根据文献[6]的分析研究结论,本文中焊点的位置如图2所示。第1个焊点距前端面10 mm,依次往后间隔50 mm布置1个,最后1个距后端面40 mm。

图2 焊点的位置布置图
在通常的车辆碰撞问题中只有少数焊点开裂,在此可不考虑脱焊,采用rigidbody模拟焊点[7]。划分好网格之后,使用rigidbody模拟焊点将两帽形构件进行连接。
1.5 仿真模型的建立
前纵梁的后端固定,即约束后端面节点的所有自由度。 以一质量为 30 kg、速度为 13.6 m·s-1的质量块撞向薄壁梁前端,并约束其除X方向自由度以外的所有自由度,即质量块在整个过程中只能沿纵梁轴向运动。
1.6 碰撞仿真分析
图3为前纵梁碰撞变形过程,时刻分别取0 ms、10 ms、20 ms、30 ms,可以看出,在碰撞初始时刻,整段纵梁都产生了较大的应力,特别是后部应力较大。前纵梁沿轴线并没有产生在对称面内的对称屈曲变形,而是产生了一定的扭曲。随着时间的延长,塌陷首先从碰撞的前端开始,前端受到冲击产生褶皱,褶皱继续被压缩,并同时在后部生成新的褶皱,后端基本无变形。
在碰撞模拟过程中,沙漏能与内能比在10%以内,沙漏能对变形计算结果影响不明显。本文的仿真计算,沙漏能与内能之比都小于10%,因此认为此网格密度是合适的,此仿真计算结果可信。在碰撞结束后,前纵梁吸能总量为2751.8 J。整个碰撞过程中,纵梁变形模式较差。折叠变形不理想,吸能效果不好。
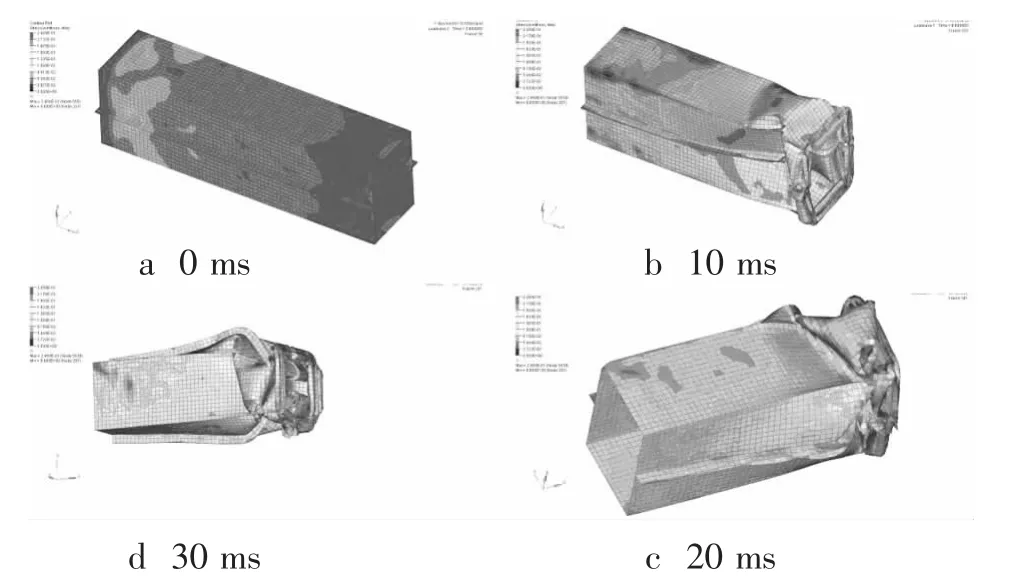
图3 不同时刻前纵梁碰撞变形情况
2 前纵梁的优化设计
为了改进前纵梁变形模式,更好的吸能,本文主要采用对前纵梁添加变形引导槽 (简称为诱导槽)。诱导槽位置不同,前纵梁在诱导槽前后的刚度比例也随之改变,从而影响了纵梁的变形模式和塌陷顺序[2]。并通过改变诱导槽的形状和诱导槽距纵梁前端面的距离来对前纵梁进行优化设计。
2.1 诱导槽的截面形状
本文建立了诱导槽的截面形状分别是弧形、V形、方形的纵梁的有限元模型。3种截面形状的诱导槽的深度相同,均为20 mm,宽度均为30 mm。
图4为质量块与不同截面形状诱导槽的纵梁接触时,纵梁的应力分布图。接触时的应力集中均出现在诱导槽附近,而后部基本没有影响。图5为不同截面形状诱导槽的纵梁的最终变形情况,可以看出三者没有太大差别。减速度—时间历程对比曲线如图6所示,3个方案的曲线形状、变化趋势基本接近,弧形和方形的初始碰撞的减速度峰值均为1.902 mm·ms-2左右,而 V 形则只有 1.5496 mm·ms-2。

图4 碰撞初始时刻应力分布

图5 最终变形

图6 3种截面形状方案的减速度—时间历程对比曲线
内能—时间历程对比曲线如图7所示,3个方案的曲线形状、变化趋势基本接近,吸能总量也均在2700 J左右。
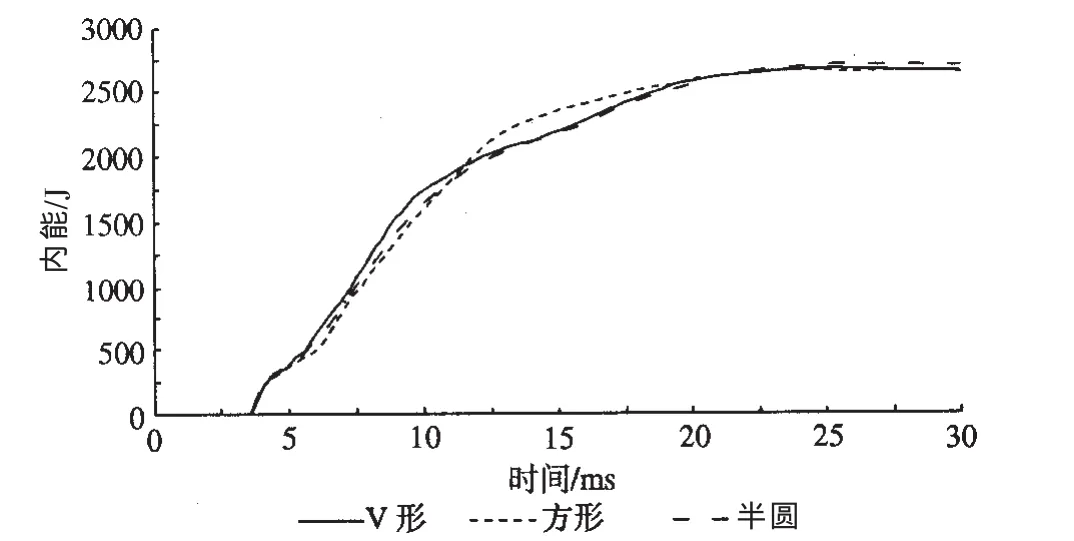
图7 3种截面形状方案内能—时间历程对比曲线
由于在诱导槽起作用的情况下,变形总是从诱导槽处开始,所以在上述对比分析中可以看出尺寸相同、但形状不同的诱导槽对纵梁耐撞性的影响没有多大的区别。最大区别在于V形槽的减速度相对于另外22个来说较小,有利于减小冲击和保护乘员安全。同时,V形槽的加工成本也较低,所以最终优化方案采用V形诱导槽。
2.2 诱导槽中线距前端面距离
改进后的模型是在原模型基础上开启了诱导槽,其余尺寸不变。在诱导槽形状(均为V形横截面)、尺寸一定的前提下,模拟诱导槽中线距纵梁前端面 30 mm、40 mm、50 mm、90 mm、170 mm、260 mm等6个不同距离时对前纵梁碰撞性能的影响。6个方案分别对应编号为 1、2、3、4、5、6。 纵梁最终的变形情况如图8所示。
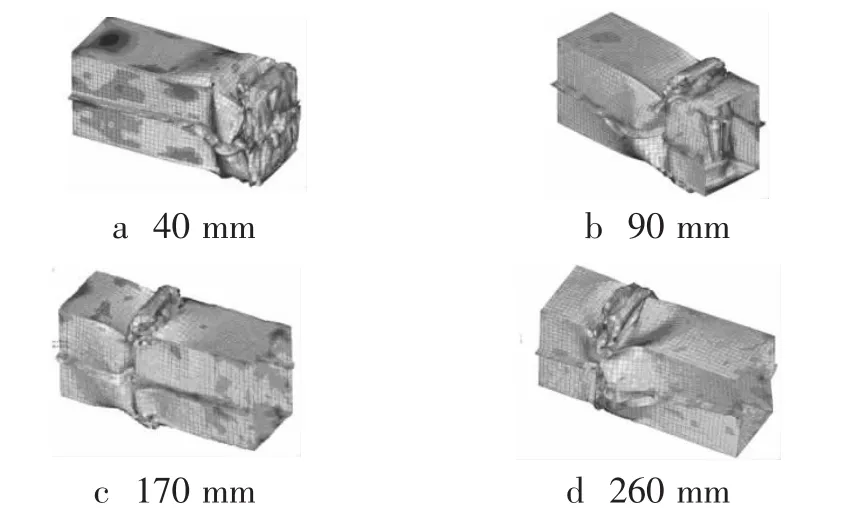
图8 纵梁最终变形情况
诱导槽中线距前端面距离为30 mm、40 mm、50 mm,这3个方案纵梁的变形相似,即变形首先从开有诱导槽的地方开始塌陷,整个变形过程保持从前向后逐渐塌陷的变形顺序,后端应力较小,故选诱导槽中线距前端面距离为40 mm的最终变形情况与后面的3种变形情况进行比较,当诱导槽位置比较靠前时(方案1~3),纵梁基本保持了由前向后的塌陷顺序,说明在压缩过程中,纵梁是以塑性铰叠缩的形式逐渐向后推行,在形成每一个叠缩的过程中,纵梁壁绕着最终形成叠缩凸点(内凸或外凸)为铰点转动并向后推行,未发生屈曲部分的纵梁壁的强度基本保持不变,使得每一个折曲的开始形成时都是一次弹性屈曲。同时,纵梁后端的应力较小,有利于降低对车身其余部件的冲击。当诱导槽靠近纵梁中后部位置时(方案4~6),纵梁的塌陷顺序发生变化,不再保持由前向后的塌陷顺序,而是从诱导槽处开始向前或向后逐渐推行,但仍然为塑性铰叠缩的变形形式。但后端的应力较大,与原始设计相比较则没有改进。
从能量吸收的角度来看,不同方案的内能—时间历程曲线的形状、变化趋势基本接近,但吸能总量有所区别。按内能由大到小排列如表1所示。前4个方案的最大减速度比原始设计的要小,而后2个则接近,方案1、2、4则相差不大。按最大减速度由小到大排列见表2。
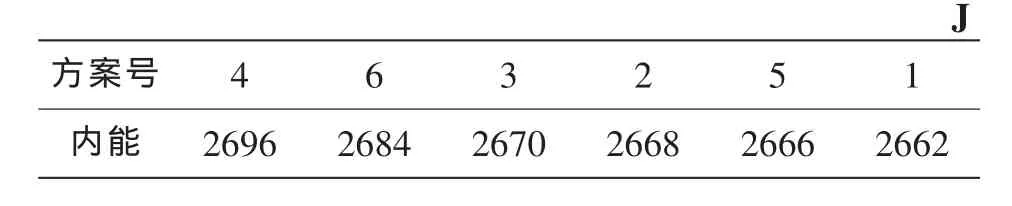
表1 不同方案的吸能总量

表2 不同方案的最大减速度
基于以上分析可以得出以下结论:
1)在诱导槽能起作用的条件下,前纵梁在碰撞中的变形总是从诱导槽处开始,若诱导槽靠近纵梁前端,则诱导槽能起到比较好的诱导作用,变形主要由纵梁前端逐渐向后部扩展;
2)从变形模式上来看,诱导槽距纵梁前端30~50 mm范围内的诱导效果较好;
3)若诱导槽位于纵梁的前端位置,则在诱导槽处先变形,接下来是诱导槽前面部分塌陷,待其变形完毕,才是诱导槽后面部分由前向后逐渐变形;
4)若诱导槽位于纵梁的中部位置,则在诱导槽处首先变形后,接下来是诱导槽后面的部分由前向后逐渐变形,待其变形完毕,才是诱导槽前面的部分由后向前逐渐变形;
5)若诱导槽位于纵梁的后端位置,诱导槽处首先变形,接下来,诱导槽后面的部分发生小变形,该部分刚性随即增加,导致诱导槽前面的部分由后向前持续变形;
根据以上分析,诱导槽中线距纵梁前端面的距离选为40 mm。
3 改进前后仿真对比分析
3.1 碰撞变形
优化前后纵梁的碰撞变形过程如图9所示(左为原始设计,右为优化方案),可以看出,优化后的前纵梁沿轴线产生在对称面内的对称屈曲变形,而原始设计的则不是,并产生扭曲。通过比较可以知道,优化后的纵梁塌陷从诱导槽开始,而原始设计则从前端面开始变形。优化后的纵梁变形比原始的要大且明显,从最终的变形形式来看,优化后的纵梁的变形模式较好。
3.2 初始碰撞时刻的应力
图10为优化前后碰撞时刻应力云图。对比分析可以知道,碰撞初始时刻,原始设计的纵梁后部应力集中明显,而优化后的则没有,这有利于减少撞击力向驾驶室的传递,有利于保护乘员安全。
3.3 碰撞界面力
从图11可以看出,原始设计和优化方案都在碰撞初始时刻(3.7 ms)左右出现界面力的第1个峰值,原始设计的峰值较大,达到102.68 kN;而优化方案的较小,只有49.539 kN。这是由于加了V形槽之后,纵梁的纵向刚度降低,减小了冲击力的峰值。在5~7 ms时间区间内,原始设计的曲线出现了比较频繁的波动,而且峰值都在40~50 kN范围;优化方案的二次峰值出现得较晚,于6 ms,为34 kN左右,虽然在8 ms左右又出现了第3个峰值,但仍为35 kN左右,整体起伏平缓。原始设计的平稳界面力保持在15 kN左右,但在13.4 ms又达到了21 kN;优化方案的界面力在平稳阶段最低达到了2.5 kN左右,整体平均为9 kN。优化方案的界面力持续时间要比原始设计缩短了0.6 ms左右。经过以上分析,结合两者的变形情况可以知道,优化方案的界面力峰值较小,起伏平缓,有利于减少对乘员的冲击伤害。
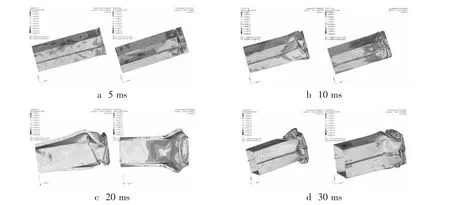
图9 优化前后的纵梁碰撞变形过程
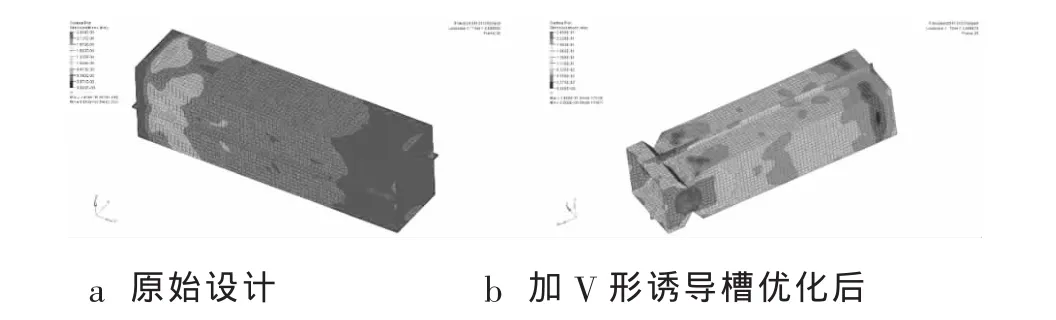
图10 优化前后碰撞时刻应力云图

图11 优化前后的界面力—时间历程对比曲线
3.4 碰撞减速度
优化前后两前纵梁(质量块)减速度—时间历程对比曲线如图12所示,可以看出,在碰撞初始时刻4.0 ms左右,两前纵梁几乎同时出现第1个减速度峰值(最大减速度峰值),原始设计的最大减速度峰值较大,大小为 3.6419 mm·ms-2,优化后最大减速度峰值相对较小,大小约为1.5496 mm·ms-2;原始设计的碰撞减速度整体变化幅度较大,在8 ms左右又出现了一个峰值,即前纵梁所承受的峰值载荷变化比较剧烈,而开V形槽后,前纵梁的碰撞减速度变化较均匀,波动相对平缓,前纵梁所承受的峰值载荷变化相对平稳,避免了反复波动对乘员造成震荡而带来二次伤害。
在高速碰撞中,碰撞过程中的平均加速度值是评价汽车碰撞性能好坏的重要指标。平均碰撞加速度反映了汽车在碰撞过程中的平均碰撞力大小,而平均加速度与碰撞时间有关,碰撞时间越长,平均加速度越低,车身平均载荷越小,碰撞安全性越好。另外,在高速碰撞过程中,总希望前纵梁的减速度具有较长的持续时间,较小的减速度峰值,以提高汽车在碰撞过程中的抗冲击性能[8]。
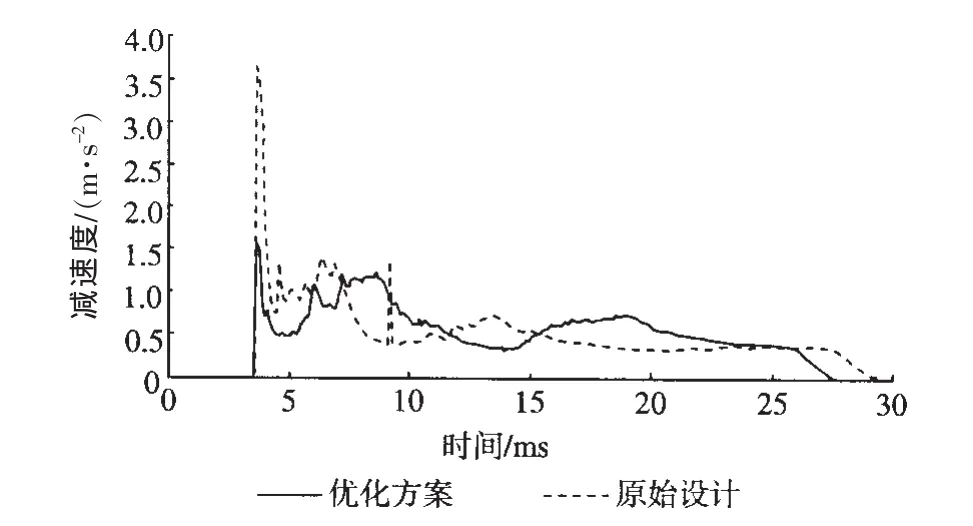
图12 优化前后的减速度—时间历程对比曲线
3.5 位 移
质量块的位移—时间历程对比曲线如图13所示,可以看出,和原始设计相比,开V形槽后,质量块在速度方向上的最大位移增大约为11 mm。由此说明,V形诱导槽对前纵梁的变形位移特性产生了很大影响,对碰撞起到了一定的缓冲作用。
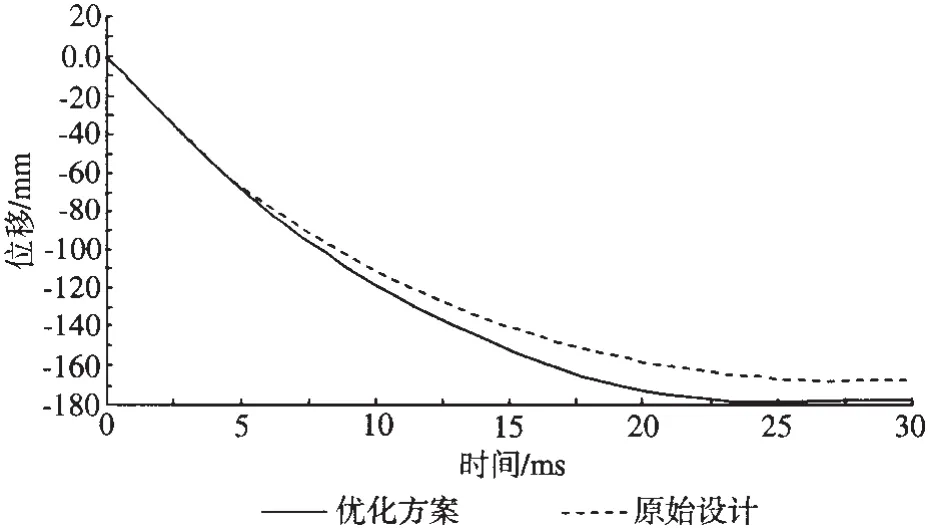
图13 优化前后的位移—时间历程对比曲线
3.6 内 能
碰撞中,质量块的动能除了摩擦消耗掉一部分,其余的全部转化为薄壁结构的内能。两前纵梁的内能—时间历程对比曲线如图14所示,可以看出,优化方案的吸能速度大于原前纵梁的吸能速度,但最后总体吸收的内能要小于原始设计。原始设计的吸能总量为2751.8 J,优化后的前纵梁吸能总量为2668.53 J。后者比前这少吸能83.27 J。吸能总量减少的最大原因是开诱导槽之后纵梁的整体刚度降低。总量虽然减少,但差值较小,仍在理想范围之内。
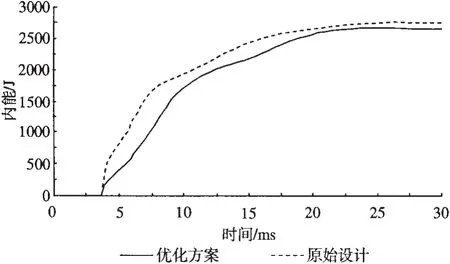
图14 优化前后的内能—时间历程对比曲线
4 结 论
利用HyperMesh和LS-DYNA软件,对长安微型车的前纵梁的正面碰撞进行了仿真模拟,其分析的结果可以用于前纵梁的安全性设计。从分析可以看出,带V形诱导槽的双帽形前纵梁在动态碰撞中:变形明显,变形模式较好;界面力峰值较小,曲线变化趋势平缓;减速度峰值较小,波动相对平稳,且持续时间较长;吸能速度较快,吸能总量与原始设计相近。上述特性可以很好地限制冲击载荷,使乘员免受高冲击力。
[1] McNay II Gene H.Numerical Modeling of Tube Crash with Experiment Comparision[J].SAE Paper:880898.
[2]刘中华.薄壁梁动态撞击的变形和吸能特性的仿真与分析[D].长春:吉林大学,2003.
[3]彭昌坤,王国业,吴阳年.汽车前纵梁碰撞特性仿真研究[J].机械研究与应用,2007(4):77-78.
[4] 柳艳杰,胡 焜,夏春艳,等.低速碰撞时汽车前纵梁的数值仿真与优化设计[J].哈尔滨商业大学学报:自然科学版,2008(24):347-351.
[5] N.Jones,T.Wierzbicki.Structure aspects of ship collisions[M].Structural Crashworthiness,1983:308-337.
[6] 解跃青,方瑞华,雷玉成.基于碰撞数值模拟的汽车纵梁焊点布置方法[J].焊接学报,2003,24(1):73-76.
[7] 郝 琪,马 迅.车辆薄壁结构碰撞性能的研究[J].机械设计与制造,2006(6):66-68.
[8] 邓召文,高 伟.基于虚拟试验的汽车40%偏置碰撞抗撞性分析[J].湖北汽车工业学院学报,2008,22(4):6-11.
