两个面积最小问题的推广

陈建华

（福建农林大学计算机与信息学院，福建福州 350002）

两个面积最小问题的推广

陈建华

（福建农林大学计算机与信息学院，福建福州 350002）

把两个有关平面图形的面积最小问题进行推广，得到较一般的情形，所求的点都是区间的中点.

曲线；面积；最小

1 第一个问题及其推广

有这样的一个面积最小问题［1］，它是1987年全国考研数四的试题：

求曲线y＝x2在［0，1］内的一个点t，使此曲线与直线y＝t2以及直线x＝0，x＝1所围成的图形面积最小.

若曲线y＝x2不变，把区间［0，1］推广到［a，b］（0≤a＜b），同样可求出相应的点t＝，它刚好也是区间［a，b］的中点.

那么，能否再把曲线作进一步的推广？

问题1 要求连续曲线y＝f（x）在［a，b］内的一个点t，使此曲线与直线y＝f（t）以及直线x＝a，x＝b所围成的图形面积最小.什么条件下，该问题相应的点t一定是区间［a，b］的中点？

定理1 设f（x）在［a，b］上连续，在（a，b）内可导且恒有f′（x）＞0（或f′（x）＜0），则问题1对应的点t为［a，b］的中点.

证只证f′（x）＞0的情形（f′（x）＜0的情形同理）.因为f（x）在［a，b］上连续，在（a，b）内f′（x）＞0，所以f（x）在［a，b］上单调增加，于是，所言的面积

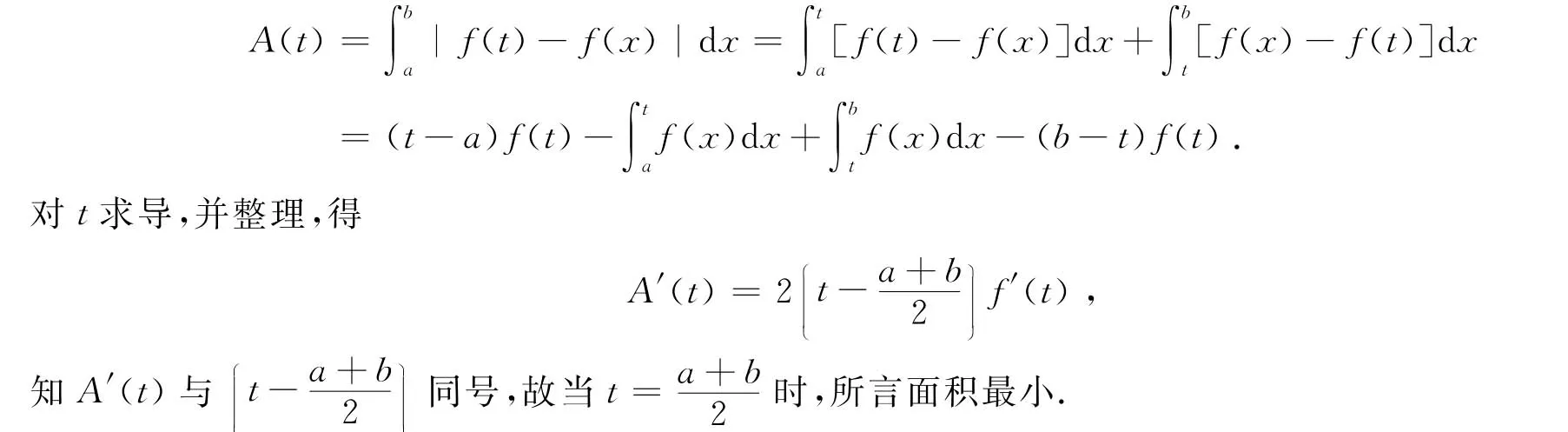
定理1表明，某区间上严格递增或递减的曲线，该面积最小问题对应的点一定是区间的中点.

对曲线y＝ex和区间［1，3］，则问题对应的点为t＝2；

2 第二个问题及其推广

下面的一个面积最小问题［1］，它是1992年全国考研数二的试题：

能否再把曲线作进一步的推广呢？

问题2 要求连续曲线y＝f（x）在［a，b］内的一个点t，使此曲线与曲线在点（t，f（t））的切线以及直线x＝a，x＝b所围成的图形面积最小.什么条件下，问题2对应的点t一定是区间［a，b］的中点？

定理2 设f（x）在［a，b］上连续，在（a，b）内二阶可导且恒有f″（x）＜0（或f″（x）＞0），则问题2对应的点t为［a，b］的中点.

证只证f″（x）＜0的情形（f″（x）＞0的情形同理）.因为f（x）在［a，b］上连续，在（a，b）内f″（x）＜0，所以f（x）在［a，b］上为凸的，曲线y＝f（x）位于切线y＝f′（t）x＋f（t）-tf′（t）的下方，于是所言的面积为

定理和推论表明，某区间上严格凹或凸的曲线，该面积最小问题对应的切点横坐标一定是区间的中点，切线函数是中点处的一阶泰勒多项式.

对曲线y＝ln x和区间［1，3］，则问题对应的点为t＝2，切点为（2，ln 2），切线为y＝x-1＋ln 2；

对曲线y＝sin x和区间［0，π］，则问题对应的点为t＝，切点为切线为y＝1.

［1］ 张友贵，杜祖缔，施光燕.掌握高等数学（理工，经济类）［M］.大连：大连理工大学出版社，2004：273-304.

O172.2

C

1672-1454（2010）增刊1-0073-02