度量空间上的位势空间容量与Hausdorff测度

陈 波,陶继成

(1.暨南大学数学系,广东广州510632;2.中国计量学院理学院,浙江杭州310018)

度量空间理论一直受到研究者的重视,众所周知,对度量空间的研究与分形的研究是紧密相关的,尤其对不确定度有重要研究[1,2].所谓度量空间就是一个非空集X相伴于一个度量或者拟度量d(x,y)满足条件:

1)d(x,y)=0当且仅当x=y,且d(x,y)≥0;

2)d(x,y)=d(y,x);

3)d(x,y)≤c(d(x,z)+d(z,y)),其中c=1,称d(x,y)为一度量,否则称为拟度量,c＞0且x,y,z∈X.

一般我们有(X,d)上的一Borel正则测度使得每个在X中的度量球的测度有限而且为正.有时称(X,d,μ)为度量测度空间,简称为度量空间,同时我们一般设测度μ满足双倍测度条件,即存在常数c＞0使得

其中B(x,r)为圆心为x、半径为r的球.称有双倍测度的度量空间为齐型空间.

我们知道关于齐型空间有个很重要的结果,R.A.Maci′as与C.Segovia在文献[3]中证明了d(x,y)等价于另外一个拟度量 δ(x,y),其中δ(x,y)具有Lipschitz连续性质.在欧氏空间中,满足Lipschitz性质的函数是几乎处处可导的,那么似乎在度量空间中也有类似性质.的确,在文献[4-6]等中,J.Heinonen与J.Cheeger等人共同建立起了度量空间中的Sobolev空间,并讨论了其相关性质.他们的讨论基本都是建立在度量空间中的某类Poincare不等式的基础上,然后建立了相应的Sobolev空间.在度量空间中,讨论空间的Hausdorff维数是一基本问题,容量的概念也是常用的,常用的是Hausdorff测度.与欧氏空间上的分析是有很大区别的,从某种角度而言,度量空间上的分析更与分形分析接近.本文建立度量空间上的位势空间,并讨论容量以及其与空间的Hausdorff测度及维数之间的联系,推广了J.Heinonen等人的结果(尤其是文献[3]中的第九章中的内容Page 68～78),度量空间上的分析及分形理论在不确定性、微分方程等方面中有重要的应用,较深入的工作有文献[6,7].

为了更好地突出论文主题思想,不妨设d(x,y)具有Lipschitz连续性质.本文结构如下:在第二部分给出度量空间上的位势空间;在第三部分给出度量空间上的位势空间的容量及其性质;在最后一部分讨论度量空间中容量与Hausdorff测度之间的联系.

1 位势空间的建立与性质

文献[8]中,P.Hajlasz和P.Koskela建立了Sobolev空间.这里可以用类似方法产生位势空间的定义.给定满足双倍条件的度量空间(X,d,μ),这里对于如果0＜α≤1且u∈Lp(X),存在0≤g∈Lp(X)

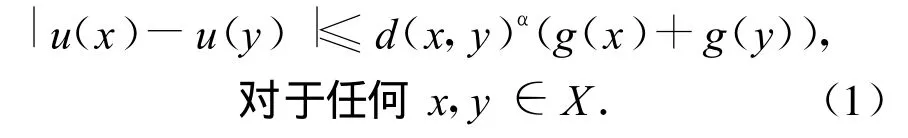
那么对于p≥1,定义位势空间Lp,α(X)空间的范数为

另外满足不等式(1)的函数 g称为函数u的Lipschitz上界.定义(X,d,μ)上的极大函数

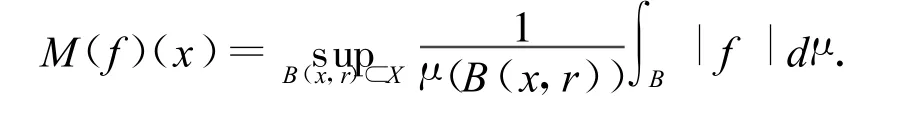
证明以下定理

定理1 给定满足双倍条件的度量空间(X,d,μ),如果1＜p＜∞,那么下列条件等价:

1)u ∈ Lp,α(X);

2)u∈Lp(X),存在c＞0,σ≥1,0≤g∈Lp(X),且 p＞κ≥1使得

其中uB表示函数u在半径为r、中心为x的球B上的平均.

定理1的证明 首先说明1⇒2,这可以从位势空间的定义及Holder不等式直接推出.所以我们只需要证明2⇒1,我们只需证明对于κ＜p使得

从极大函数的有界性质,可以得到1)只需要证明对于给定球体B=B(x,r0)(r0=d(x,y))

因为如果得到式(5),那么也可以类似得到

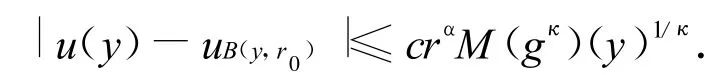
另外由测度的双倍性,也可以得到

所以,根据上面的证明可以得到式(4)(5)的证明是标准的,因为在齐型空间中,依然有对于u∈Lp,在几乎处处意义下,

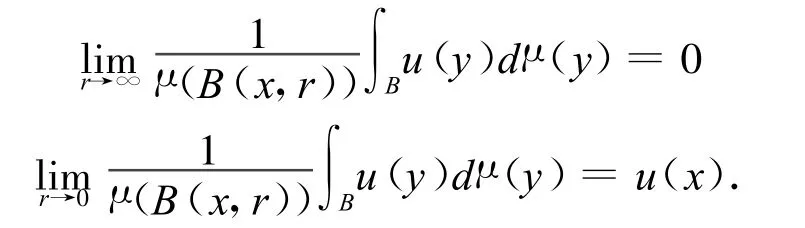
所以

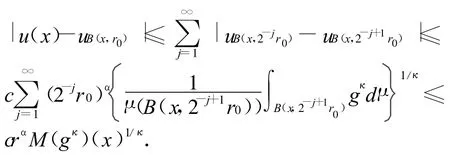
也就证明了式(5),定理证毕.

2 度量空间上的容量

设(X,d,μ)上的 Riesz位势算子,即分数次积分为我们用Riesz位势算子来定义度量空间上的容量.

定义1 设K是X上的子集,那么定义在X上的Riesz-p容量可以定义为

其中f是度量空间上的非负函数,M是K的一个邻域.

在讨论的过程中,一般设X是正则的,也就意味着X中的任意闭球都是紧的;另外我们一般假设 μ(X)=∞.证明下列结果.

命题1 设f∈Lp(X)(1＜p＜∞)为X上的非负函数,那么如果 μ(B(x,d(x,y)))关于x和d满足Lipschitz性质,即存在β＞0使得|μ(B(x,d(x,y)))-μ(B(z,d(z,y)))|≤

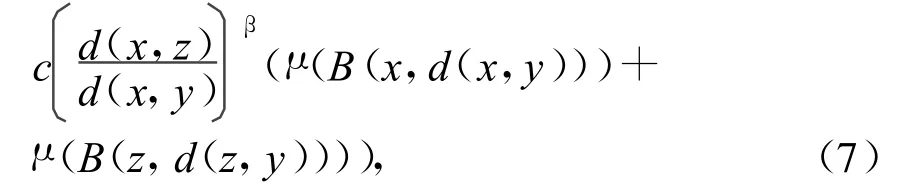
其中x,y,z∈X.即可得到存在某常数β′＞0且0＜α＜β′使得 Iα(f)∈ Lp,α(X).

命题1的证明 首先说明由于d(x,y)也具有Lipschitz连续性质,那么易得存在β′＞0使得

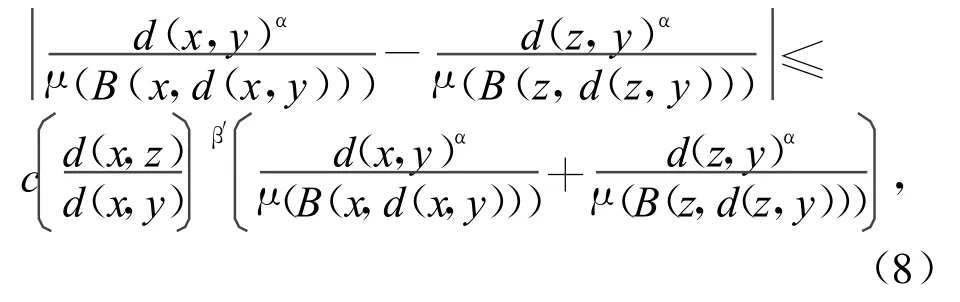
要证明 Iα(f)∈ Lp,α(X),只需验证 Iα(f)满足式(3),只需证明存在常数c,κ＞1使得,这里不妨设f≥0,

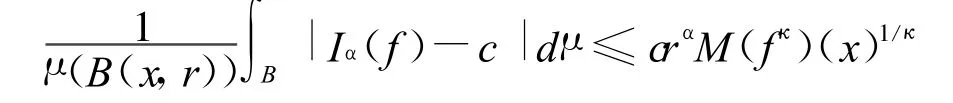
其中r是球B 的半径.让 f=fχ2B+f χ(2B)c=f1+f2,c=(Iα(f2))B,那么

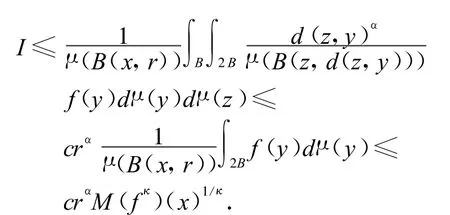
另外

那么

也就证明了命题.

注1 如果 μ(B(x,d(x,y)))=d(x,y)s(s＞1),那么式(8)由于d(x,y)具有Lipschitz连续性质也就成立,但这里仍然不能证明一般齐型空间上的测度是否满足式(8).另外知道传统方式来定义度量空间上的容量是:

定义2 设K是X上的子集,那么定义在X上的Riesz-p容量可以定义为

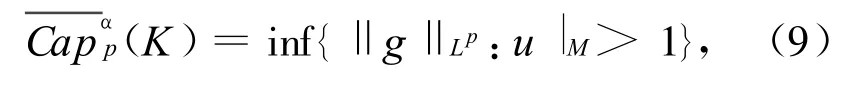
其中u∈Lp,α(X)是度量空间上的非负函数,而g为函数u的Lipschitz上界,M是K的一个邻域.

注意到正因为命题1,我们给出的定义1是合理的,但这里遗憾的是还不能说明如果u∈Lp,α(X),u是否是g的分数次积分,这也导致现在不能判断定义1与定义2是否等价.

根据命题1,所以可以另一类分数次函数空间.

另外定义K集上的一集类

其中M是K的一个邻域.

还可以得到下面关于Riesz-p容量的性质.

命题2 设1＜p＜∞,X上的Riesz-p容量是外测度.

那么测度的可数可加性即得.因为对应每个Ei,存在函数 ui=Iα(gi)∈ Α(Ei),且

证明完毕.

3 度量空间上的Hausdorff测度

度量空间上的 Haussdorff测度与其维数定义如下:

那么E的Haussdorff测度定义如下

E上的Haussdorff维数定义为

一般称测度μ是m-正则的,如果存在ν＞0,c≥1使得

其中x∈X.我们知道μ的维数就是ν,在此条件下,如果ν＞α,那么命题1自然成立.那么在此条件下有以下定理:

定理2 设1＜p＜ν且0＜α＜β′,E是度量空间X上的紧集,且测度μ满足式(10)且双倍条件为

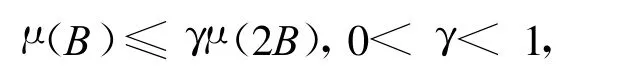
在证明定理2之前,需要以下引理

引理1 设条件如上定理所设,E是紧集,0＜ν-s＜pα,u∈ Α(E),那么对于 x∈ E有

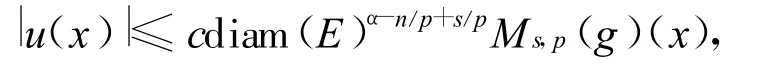
其中diam(E)表示E的直径,不等式在几乎处处意义下成立,另外

引理1的证明 对于u∈Α(E),不妨设E⊂B(x,R),这里 2R ～diam(E),那么对于 u∈Α(E),有

因为 μ(B)≤ γ μ(2B),所以也就得到

那么

证明完毕.

有了上面的引理,定理2的证明也就容易了,

定理2的证明 我们已经知道Ηs(E)=0当且仅当Ηδs(E)=0(0＜δ≤∞),所以只需要证明当s＞ν-pα,Η∞s(E)=0,那么定理得证.而要证明之,只需要证明对于t＞0有

这是因为引理1以及下面的结果

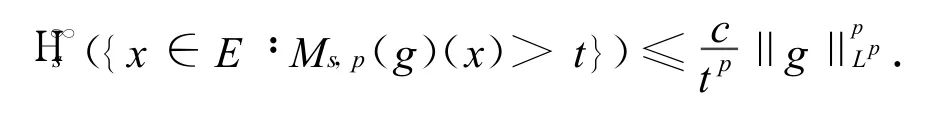
上面的结果可以由Hausdorff测度的定义以及Vitalli覆盖引理得到,读者可以参考文献[9]中引理2.29的证明.有了式(11),定理2也就得到了,证明完毕.

[1]王斗文,黄道臣,赵守成,等.AAS测量体系线性校正下的不确定度受控分析[J].中国计量学院学报,2004,15(2):108-112.

[2]刘智敏.扩展最大熵原理及其在不确定度中的应用[J].中国计量学院学报,2010,21(1):1-5.

[3]MACIAS R A,SEGOVIA C.Lipschitz functions on spaces of homogeneous type[J].Adv in Math,1979,33(3):257-27.

[4]HEINONEN J.Quasiconformal maps in metric spaces with controlled geometry[J].Acta Math,1998,181(1):1-61.

[5]HEINONEN J.Lectures on analy sis on metric spaces[M].New York:Universitext Springer-Verlag,2001.

[6]CHEEGER J.Differentiability of Lipschitz functions on metric measure spaces[J].Geom Funct Anal,1999,9(3):428-517.

[7]赵 琼,韩亚州.Heisenberg群上次拉普拉斯不等方程弱解的不存在性[J].中国计量学院学报,2010,21(1):78-81.

[8]HAJLASZ P,KOSKELA P.Sobolev met poincare[M].M em Amer Math Soc,2000,145(688):1-70.

[9]HEINONEN J,KIPEAINEN T,MARTIO O.Nonlinear potential theory of degenerate elliptic equations[M].New York:Oxford Science Publications,1993:10-40.