具有类反斜线回滞系统的自适应控制

祝建伟,陈彭年

(中国计量学院机电工程学院,浙江杭州310018)

迟滞现象(Hysteresis)又称回滞现象或滞后现象,是指一个系统的系统状态不仅与当下系统的输入有关,而且会因其过去输入过程路径不同而有不同的结果.换而言之,一个系统经过某一输入路径运作之后,即使换回到最初状态值时的同样的输入值,系统也不能回到其初始状态.迟滞现象无论在物理实验中还是在现实工程中都是广泛存在的,例如在伺服系统[1]、电子电路等机械电子设备、超导材料、压电陶瓷、智能材料等具有记忆功能的材料以及电磁场中[2,3]均存在.

由于具有不可微的非线性,回滞现象的存在会严重限制系统的性能,引起系统震荡,造成系统不稳定.而削弱乃至消除具有不可微的非线性的环节又是比较困难的,因此如何控制具有回滞环节的系统便成了一个长期以来难以解决的课题.

针对这类问题,通常的一种控制方法是构造一个与系统级联的回滞环的逆模型进行前馈控制,直接抵消或者削弱回滞环带来的影响[4-6].这类方法的一个问题是由于需要在回滞环上行和下行曲线上分别进行控制,构造出的逆模型也是个回滞环.回滞环解一般都极其复杂,大部分控制方法还不能进行稳定性分析[3].另外,在采用自适用逆法对回滞进行控制时,还有一个特殊的问题就是其逆通常并不是唯一的,选择不同的参数往往会取得执行结果上很大的差异,而且在跳转过程中会造成系统的抖动.

本文将研究一类具有类反斜线回滞的非线性不确定系统的自适应跟踪问题.虽然文献[7]研究过类似的问题,但其方法不能保证跟踪误差任意地小.本文的方法可保证跟踪误差小于任意给定的正数.

此外,还将介绍两种比较简单实用的基于神经网络的自适应控制方案.在本文的第二部分首先对问题进行了说明.第三部分基于反步法提出了控制方案并进行了稳定性分析.第四部分的仿真说明了所提出的方案的有效性.第五部分对这篇文章进行了小结.

1 问题描述

考虑下面一类不确定非线性系统:

其中,x=(x1,x2,…xn)T∈Rn为代表系统状态的一个n维向量,y∈R为系统输出,ω(u)为执行器输出,f(x)和g(x)是Rn上的未知连续函数,代表系统的不确定性.执行器 ω(u)是控制输入u通过一个类反斜线回滞滞后环节形成的,其数学表达式为

其中α,c,B1都是常数,c＞0为直线部分的斜率且满足c＞B1.则系统(2)的解可以表示为

其中

对于系统的不确定性g(x)作如下假设:

假设1 存在正常数g1,g2,使得g2≥cg(x)≥g1＞0.

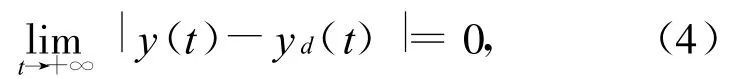
或

其中,ε＞0是任意给定的常数.

2 自适应控制器的设计

为设计控制器,首先导出跟踪误差方程.设

则跟踪误差方程为

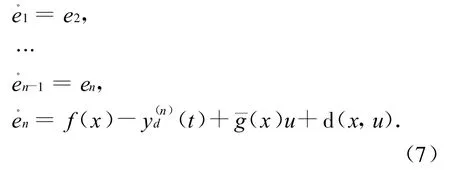
其中¯g(x)=cg(x),d(x,u)=g(x)d(u).对于系统的不确定性d(x,u)依文[1]我们作如下假设:

假设2 存在正常数dmax,使得d(x,u)≤dmax

为方便设计,将系统(7)改写成向量形式.设e=(e1,e2,…,en)T,则系统(7)可以改写为

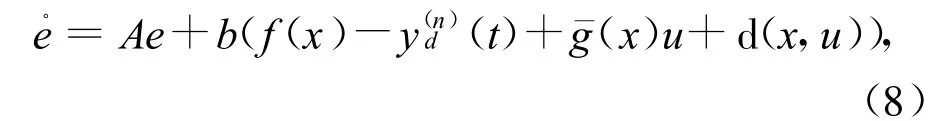
其中

因为f(x)是非参数化的未知函数,因此通常需要用权系数未知的神经网络对其进行逼近.设ρ＞0和

本文采用径向基函数神经网络,该网络具有良好的非线性映射能力[8,9],表示形式简单、隐层到输出层为线性关系、收敛速度快等优点.因为f(x)¯g-1(x)是Rn上的连续函数,根据神经网络对连续函数的万有逼近性质,对任意给定的ε＞0,存在神经网络 wTξ(x)使得

其中ξ(x)∈Rl是网络的基函数向量,w∈Rl是网络的权向量.

介绍二类自适应控制器的设计方法:一类是变结构自适应控制器设计,另一类是连续自适应控制器设计.

2.1 变结构自适应控制器的设计

变结构控制器具有较强的鲁棒性,即使对象结构参数有一定变化控制系统仍然具有较好的控制特性[10],因此,首先考虑一种变结构控制器.

设k∈Rn使得Ak=A-bkT为Hurwitz矩阵.设取定n×n正定对称阵Q,则存在对称正定阵P＞0,使得

设θ1=g2‖w ‖,θ2=dmax,其中dmax和 w分别由假设2和式(10)给出.设和分别是θ1和θ2的估计.

对系统(1)设计如下的变结构自适应控制器:

现在考虑系统的闭环稳定性.

定理1 考虑由式(8)和式(12)组成的闭环系统.设假设1和2分别成立,设x(t)⊂Ωρ,t≥0.则闭环系统的所有信号有界,且

证明 系统(8)可以改写为作李亚普诺夫函数

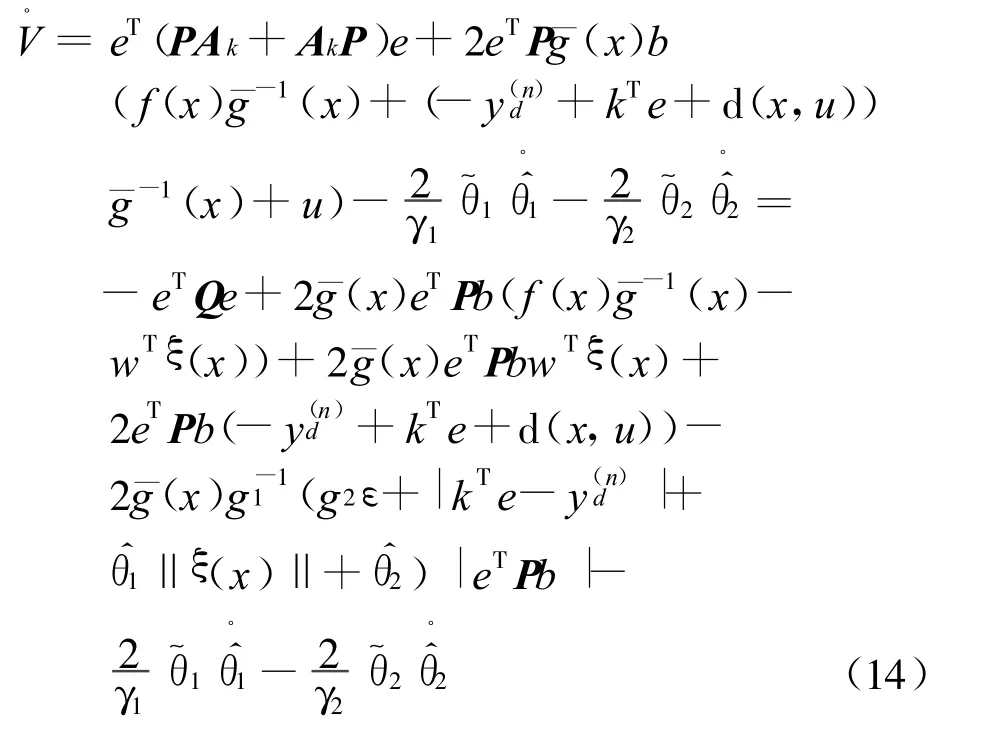
容易看到

另外

由式(14),(15)和式(16)得

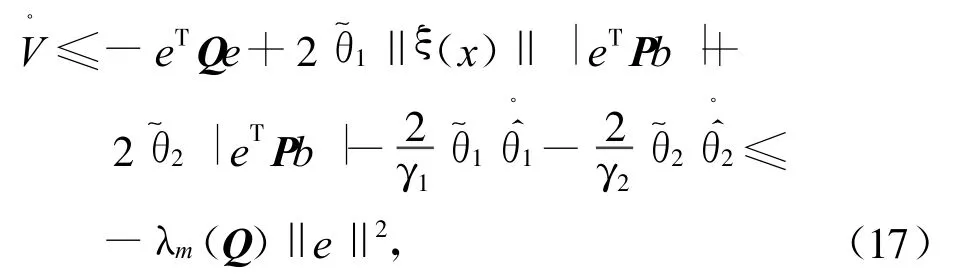
其中λm(Q)＞0为Q的最小特征值.从式(17)可知,闭环系统的所有信号都有界,而且

2.2 连续自适应控制器的设计

尽管有良好的鲁棒性,但是由于控制律中存在开关项sgn(eTPb),它产生的时滞以及惯性可能引起抖动现象.在自适应跟踪频率比较高的信号时,为了避免这种现象,这一小节再考虑一种连续型的控制器的设计.需要下面的引理.

引理1([3])设η＞0.则有

其中σ≐0.278 5.

设控制器为

定理2 考虑由式(8)和式(19)组成的闭环系统.设假设1和假设2分别成立,设x(t)⊂Ωρ,t≥0.则闭环系统的所有信号有界,且

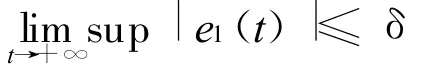
其中

证明 作李亚普诺夫函数

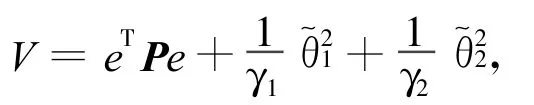
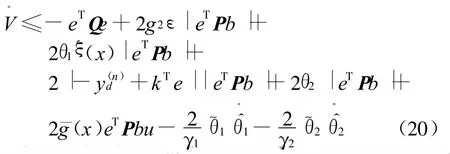
把式(21)代入式(20)可得

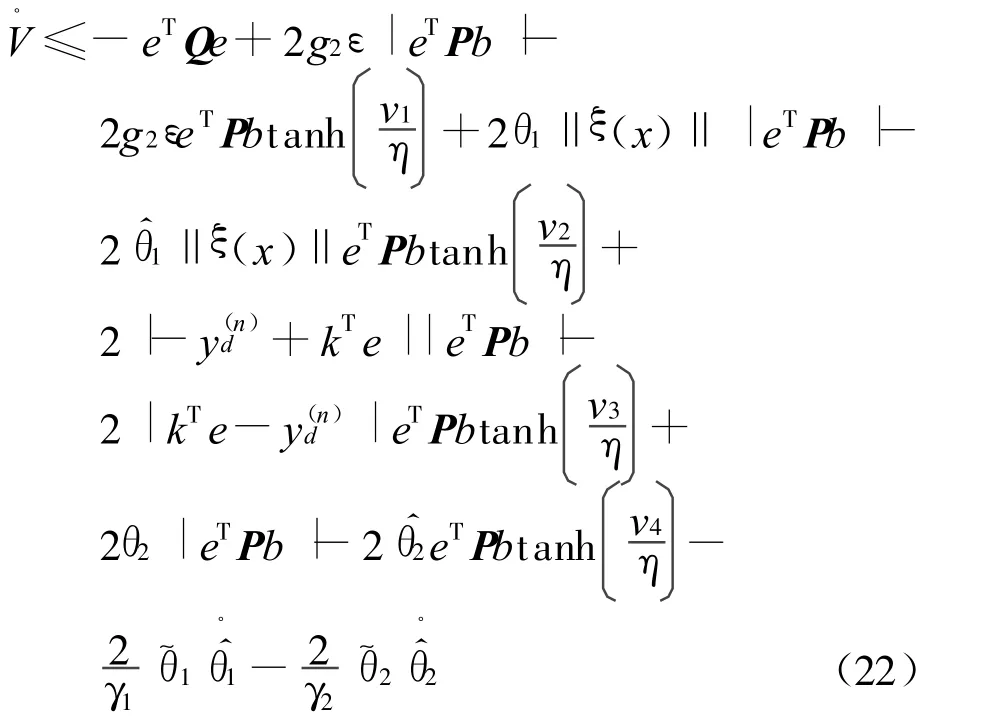
根据引理1,

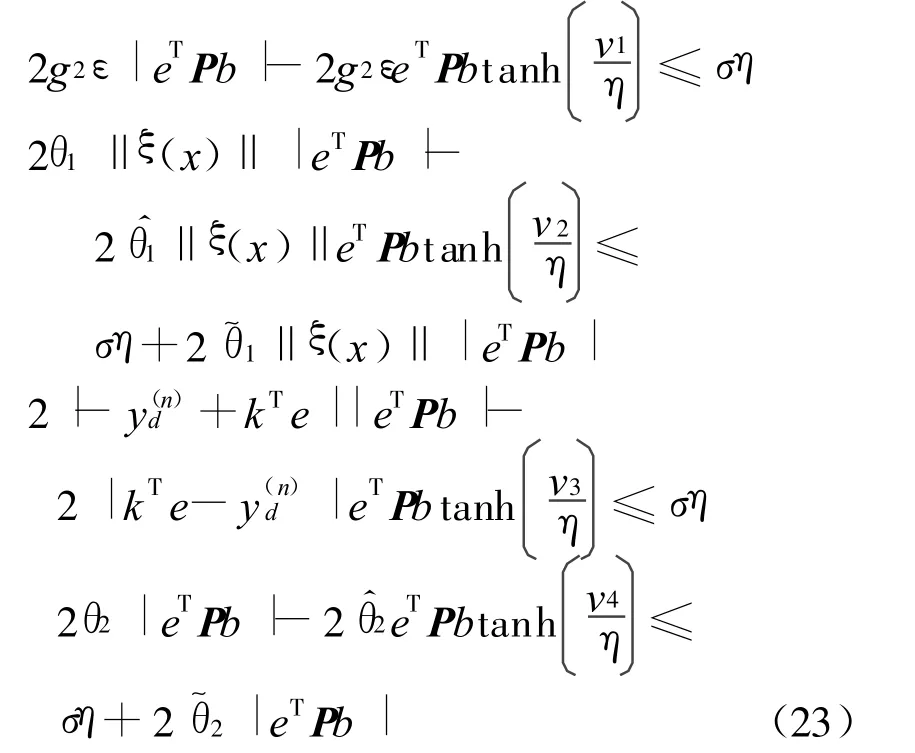
由式(19),(22)和式(23)得

陪伴洛丽塔十年的雨果死了，对于海洋馆来说，只不过是少了一头表演的虎鲸，可是对于洛丽塔而言，它不仅少了“老公”，也少了一个玩伴，它整天郁郁寡欢，拒绝进食，也拒绝表演，工作人员只好清理了水池，给洛丽塔放了几天假。

容易看到

其中λM(P)是P的最大特征值.由式(24)和式(25)立即得到

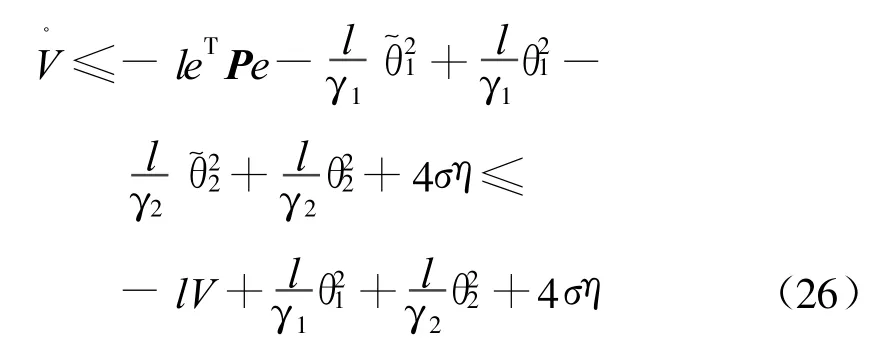
解不等式(26)可得:闭环系统的所有信号都有界 ,且

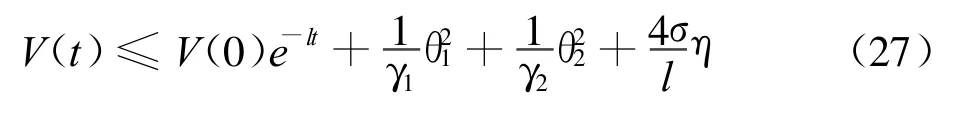
设λm(P)是P的最小特征值,立即得到

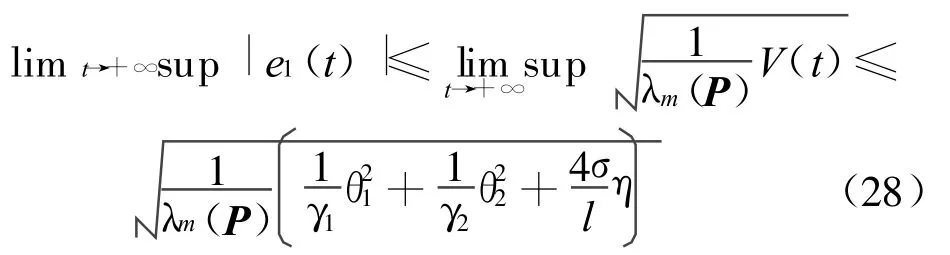
定理2证毕.

注1 由定理2知,只要适当增大γ1和γ2,减小η,则可使最后的跟踪误差小于任意给定的正数.而文献[7]公式(29)说明文献[7]的方法只能使跟踪误差小于一个给定的范围.

3 仿真研究

为了验证所提出控制方法的有效性,考虑如下非线性系统

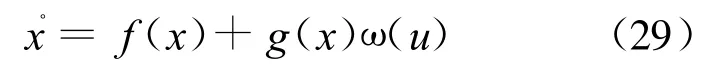
其中 x∈R,ω(x)由(2)定义.在仿真中不妨选取 g(x)=4+sinx,α=1,c=3.18,B1=0.35,控制目标是使系统状态 x(t)跟踪参考轨迹yd(t)=8sin(2t).

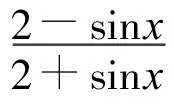
于是(29)所给系统的控制律可取为

取 η=0.02,γ1=4,γ2=10

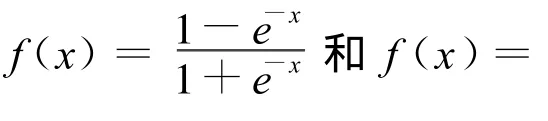
图1 f(x)=时控制输入,系统状态以及跟踪误差随时间变化曲线Figure 1 Control signal,systems status and tracking error when f(x)=

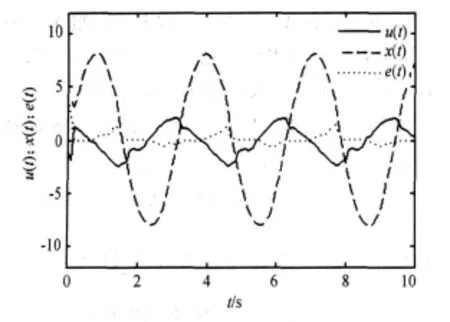
图2 f(x)=时控制输入,系统状态以及跟踪误差随时间变化曲线Figure 2 Controlsignal, systems status and tracking error when f(x)=

4 结 语

与执行器回滞相级联的非线性系统的控制是控制理论与工程上的一个难题,文中针对具有类反斜线回滞的单输入单输出非线性系统,基于神经网络的万有逼近思想,提出了两种比较简单实用的控制方案.不同于自适应逆方法,该两种方案并不需要构造一个通常很复杂的逆来抵消回滞环对系统的影响;而且在第二种方案中,证明了只要适当的调节某些参数,就可以使误差小于任何给定的正数.另外,仿真实验表明,该控制方案对于系统非线性部分的不确定性具有很好的鲁棒性.

由于类反斜线回滞在机械系统特别是齿轮系统以及压电陶瓷等中的普遍存在,该两种方法具有一定的实际应用价值.

[1]SU C Y,ST EPANENKO Y,SVOBODA J,LEUNG T P.Robust adaptive control of a class of nonlinear systems with unknown backlash-like hy steresis[J].IEEE Trans Automat Control,2000,45(12):2427-2432.

[2]ZHOU J,WEN C Y,ZHANG Y.Adaptive backstepping control of a class of uncertain nonlinear systems with unknown backlash-like hy steresis[J].IEEE T rans Automat Control,2004,49(10):1751-1757.

[3]张达科,胡跃明,郭华芳.基于Ackermann's formula的类反斜线回滞系统滑模控制[J].机械工程学报,2005,41(1):11-15.

[4]AHAM AD N J,KHO RAMI E.Adaptive control of systems with backlash hysteresis at the input[C]∥Proc Amer Control Conf.USA:IEEE,1999:3018-3022.

[5]SUN X,ZHANG W,JIN Y.Stable adaptive control of backlash nonlinear sy stems with bounded disturbance[C]∥Proc 31st Conf Decision Control.USA:IEEE cattrol syslea society,1992:274-275.

[6]TAO G,KOKO TOVIC P V.Adaptive control of plants with unknown hysteresis[J].IEEE T rans Automat Contr,1995,40:200-212.

[7]CAO H,DU H B,WANG H Z.Stable adaptive NN control for nonlinear systems preceded by un-known backlashlike hysteresis via modified VSC approach[C]∥Proceeding s of the 8th World Congress on Intelligent Control and Automation.China:IEEE,2010:554-5658.

[8]王兰州,李 峤,李东升.菊花微弱信号的神经网络预测[J].中国计量学院学报:2007,18(1):44-48.

[9]王兰州,李 峤.燕子掌微弱电信号的计量研究[J].中国计量学院学报:2009,20(3):195-200.

[10]黄振海,钟绍俊,谢 敏,等.神经网络变结构在液压伺服系统控制中的应用[J].中国计量学院学报:2005,16(3):199-202,211.