每层3个节点的神经网络对连续函数的逼近

张国平,谢庭藩

(中国计量学院理学院,浙江杭州310018)

熟知,人们常用单隐层前馈人工神经网络来逼近连续函数.其实质是当激活函数满足一定条件时,对于给定的连续函数随着网络中节点(神经元)个数的增加,该网络可以逼近此函数到任何预先给定的程度.

1989年G.CYBENKO在文献[1]中提出以S型函数为激活函数的神经网络可以逼近连续函数.1992年CHEN D B在文献[2]中用构造的方法计算以S型函数为激活函数的神经网络对单变数连续函数的逼近度.2008年CAO F L,XIE T F,XU Z B构造了一种单隐层神经网络并估计它对连续函数的逼近误差[3].当然,也有一些工作是用两个隐层而使节点个数趋向于无穷的网络来达到逼近连续函数的目的,参见文献[4-6].

本文在第二部分介绍了一些要用到的记号和定义.在第三部分给出一维情况下多层神经网络的构造方法.在第四部分给出一个应用实例.在第五部分给出多维情况下网络的构造方法,并在本文的最后部分给出附录.

1 记号和定义

本文中要用到的一些记号和定义:

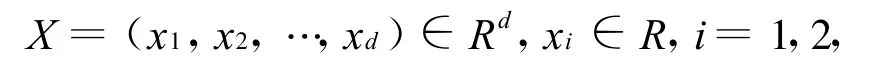
[11]中MLP网络的定义,我们定义如下的MLP*网络:

定义 函数σ∶R →R,假定d,d′和k≥1.称函数 f∈ MLP*(d,d′,σ,k,L)当且仅当f∶Rd→Rd′,存在权值矩阵V1 ∈ Rk×d,Vj ∈ Rk×k,1 ＜j＜L,VL∈ Rd′×k以及阈值向量 τj,τ′j∈ Rk×1,1 ≤j ＜L 和τL,τ′L ∈ Rd′×1.对任意的 X ∈ Rd,当向量aj和bj有如下的定义时:

有f(X)=bL.

由以上定义不难看出该M LP*网络每层的节点个数最多为k个.正如G.GRINPENBE-RG所言,只需考虑d′=1的情形就能得到该网络的逼近性质.

2 主要工作

因为d′(d′≥1)维输出的前馈人工神经网络可以看作d′个相同结构的、只是系数不一样的、一维输出的前馈人工神经网络的组合,由于其各自的独立性,只需要考虑d′=1的情况就能得到多维输出的情况.

现在给出本文的主要结论:

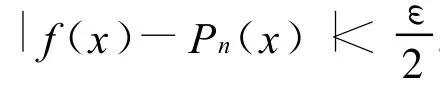
如何构造这个前馈人工神经网络 N(x).为简单不妨假设[a,b]为[-T,T].又从σ″(x)在τ*点的领域内连续且σ″(τ*)≠0,(由附录部分的引理 2)不妨取 τ* 使得 σ(τ*)≠0,σ′(τ*)≠0,σ″(τ*)≠0都成立.具体的构造过程如下.首先,给出一个构造n次代数多项式Pn(x)=cnxn+cn-1xn-1+…+c0的过程:

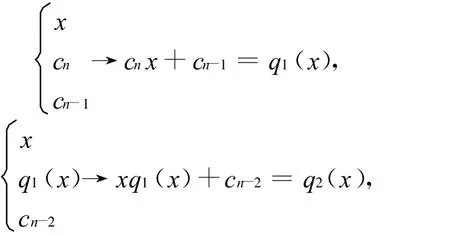
一般是输入为x,qk(x),cn-k-1,输出为xqk(x)+cn-k-1=qk+1(x),即

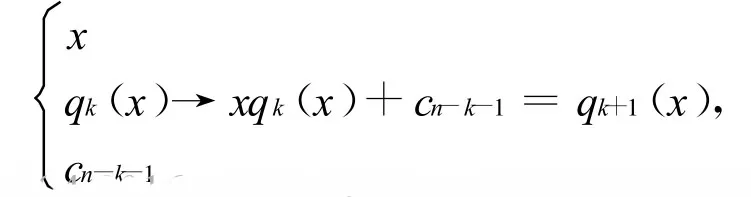
现在用n层每层3个节点的以σ为激活函数的前向人工神经网络来实现上述过程.根据定义构造一个每层2个输入3个节点2个输出的多层前馈人工神经网络MLP*的结构如下.记第j层的输入为xj,Nj(x),三个节点(神经元)为 σ(η xj+τ*),σ(η Nj(x)+τ*),σ(η(xj+Nj(x))+τ*),输出为 xj+1,Nj+1(x),其中

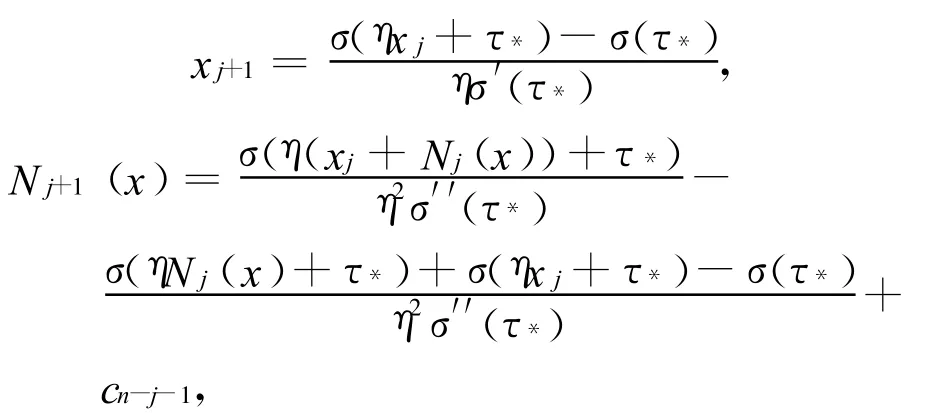
网络结构示意如下:

这里cn-j-1为多项式Pn(x)的第n-j-1项系数,初始值x0=0,N0(x)=cn.

由附录部分的引理3,对任意的 μ∈(0,1),若对任一多项式qj(x),使得在|x|≤T时第j层的输入xj,Nj(x)满足

则存在 η＞0,使得第 j层的输出 xj+1,Nj+1(x)满足如下的不等式

将上述这种2个输入3个节点2个输出的网络记作Φ.由输入x0=0,N0(x)=cn和常数cn-1通过网络Φ即得到输出x1,N1(x),且满足如下不等式

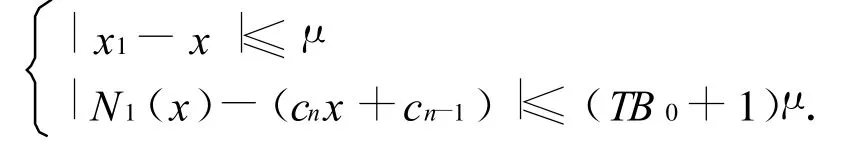
然后以x1,N1(x)为输入再次进过网络 Φ得到x2,N2(x).如此通过n层网络Φ得到的输出Nn(x)就是多项式Pn(x)的一个逼近工具.事实上,按上述过程,我们有与μ及x有关的正数Bn使得

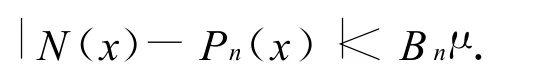
如此,若取μ＞0适当小即有

定理1证毕.

注记1:若令初始状态为L=0,q0(x)=cn,B0=0,由引理3直接得到

其中

qi(x)=cnxi+…+cn-i+1x+cn-i,i=0,1,…,n.于是不难得到

其中

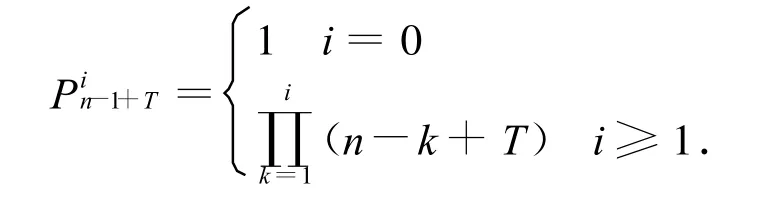
3 一个例子

我们用数据计算来模拟在一维情况下用第三部分的网络对连续函数的逼近情况.首先,把目标连续函数展开为最高次数为n的Bernstein多项式,然后用第三部分得到的网络来逼近此多项式,以此达到逼近目标连续函数的目的.所有的计算都是在MATLAB中实现的,相关程序省略.

设定目标连续函数为 f(x)=sin(πx),x∈[0,1].记Bn(f,x)为关于函数 f(x)的最高次数为n的Bernstein多项式,有

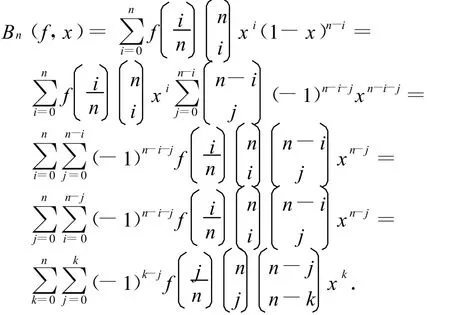
由上式不难得到

则有Bn(f,x)=c0+c1x+…+cnxn.

图1 n=10,μ=0.003 125Figure 1 n=10,μ=0.003 125

4 一般情况

为了区别,记这里所提及之网络为M LP**.在一般情况,我们有如下的

由第六部分的引理1将总次数为n的d元代数多项式Pn(x)写作

这里X∈Rd,Wj∈Rd,C0,Cl,j∈R.

构造的网络对给定多项式的逼近过程如下

下面介绍此MLP**网络的逼近过程:

第一步,利用MLP*网络逼近多项式P*n(X1)得到输出Z1(Z1≈P*n(X1)).由于 X1与 X2的相互独立性,可以把此时网络的输出Z1作为下一个多项式Pn(X2)的常数项形成一个新的多项式

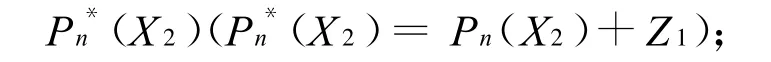
第二步,再次用MLP*网络来逼近多项式Pn*(X2)得到输出Z2(Z2≈Pn*(X2)).再把Z2作为下一个多项式Pn(X3)的常数项形成一个新的多项式

显然如此达到用MLP**网络逼近多项式Pn(X)的目的,使得此MIP**网络逼近给定的连续函数.定理2证毕.

如前所述,d′维输出的前馈人工神经网络对多项式的逼近只是d′个相互独立的一维输出的前馈人工神经网络对多项式的各自逼近,由此得到

5 附 录

本文第三、五两个部分中用的一些结论的数学证明.为此,我们需要如下的三个引理.

这是文献[12]中得到的结果.

引理2 函数σ∈C(R;R)在一点的邻域上有不恒为零的二阶连续导数,则在此邻域中有一点τ*使得 σ(τ*)≠0,σ′(τ*)≠0,σ″(τ*)≠0.

证明 显然,在引理假设下有一个开区间Δ⊂R,在Δ中σ″(t)≠0.从而Δ中必有一个子区间 Δ1⊂Δ使得在 Δ1中 σ′(t)≠0.同理 Δ1必有子区间 Δ2使得在 Δ2中σ(t)≠0.因此,对任τ* ∈ Δ2 都有 σ(τ*)≠ 0,σ′(τ*)≠0,σ″(τ*)≠0.

引理3 设σ(t)在开区间Δ中二次连续可微,而且有 τ* ∈ Δ使得 σ′(τ*)≠0,σ″(τ*)≠0.又记

其中c是个常数.如果当|x|≤T时有

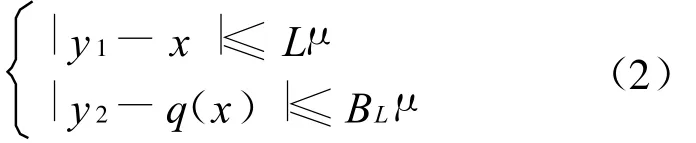
其中 μ＞0,η＞0,q(x)是关于 x的连续函数,那么只要η充分小就有

证明 本文第三部分所构造网络第j+1层的权值矩阵和阈值向量分别为:

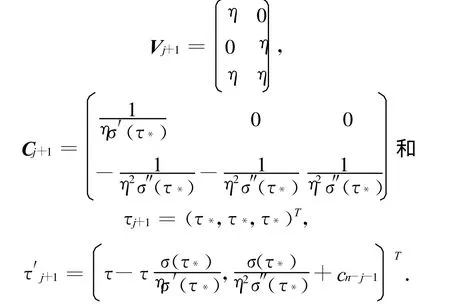
网络在第j+1层的输出为:

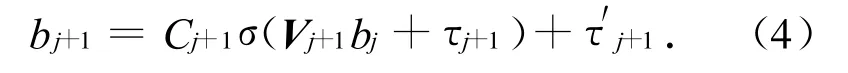
由(4)式即可得(1)式.

下面来证明(3)式.当 η＞0充分小时,由中值定理容易知道下面两式

和

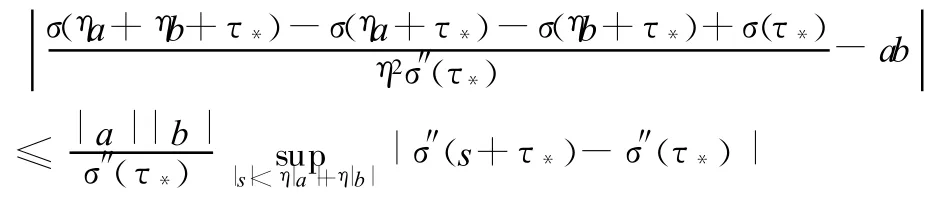
是显然成立的.

在(2)式中,

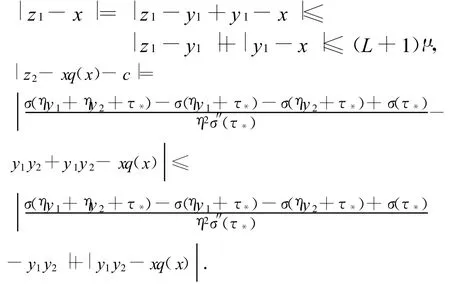
且

考虑到μ∈(0,1)且η充分小时,由上面三式及(2)式容易知道(3)式是成立的.

【参 考 文 献】

[1]CYBENKO G.Approximation by superpositions of sig-moidal function[J].Math Control Signals Syst,1989(2):303-314.

[2]CHEN D B.Degree of approximation by superpositions of a sigmoidal function[J].Approximation Theory and its Application,1993,9(3):17-28.

[3]CAO F L,XIE T F,XU Z B.The estimate for approximation error of neural networks:A constructive approach[J].Neurocomputing,2008,71:626-630.

[4]M AIOROV V,PINKUS A.Lower bounds for approximation by MLP neural networks[J].Neurocomputing,1999,25(1-3):81-91.

[5]M HASKAR H N.Approximation properties of a multilayed feedforward arT IF;%95%94icial neural network[J].Advances in Computational Mathematics,1993(1):61-80.[6]HORNIK K.Approximation capabilities of multilayer feed forward networks[J].Neural Networks,1991(4):251-257.

[7]夏哲雷,刘大键,钱 勤.人工神经网络在电积锌工艺中的应用[J].中国计量学院学报,1999,2(19):87-89.

[8]黄镇海,钟绍俊,谢 敏,等.神经网络变结构在液压伺服系统控制中的应用[J].中国计量学院学报,2005,16(3):199-211.

[9]冯会真,夏哲雷,林志一.基于神经网络的图像边缘检测方法[J].中国计量学院学报,2006,17(4):289-291.

[10]G RIPENBERG G.Approximation byneural networks with a bounded number of nods at each level[J].Journal of Approximation Theory,2003,122:260-266.

[11]CHUI C K,LI X.Approximation by ridge functions and neural networks with one hidden layers[J].J Approximaton Theory,1992,70(2):131-141.

[12]XIE T F.The ridge representation of polynomials and an application to neural netwo rks[J].Acta Mathematica Sinica,2010,26(7):1-9.