基于Beta样条曲线的等高线绘制研究

盛庆红

(南京航空航天大学 航天学院,江苏 南京 210016)

基于Beta样条曲线的等高线绘制研究

盛庆红

(南京航空航天大学 航天学院,江苏 南京 210016)

等高线须以相似的光滑曲线逼近实际地貌形态,并综合地形在一定限度内的地势起伏,其智能化控制对地貌表达具有重要的实用价值。绘图员绘制曲线时能凭经验捕捉到数据点所包含的几何形状信息,而张力样条函数和三次B样条曲线在节点插值时,严格要求二阶参数连续,不符合人的经验直觉,是节点对参数曲线连接光滑度的过分限制。根据人工绘制等高线的规则,提出将三次Beta样条曲线作为基于人工绘制约束的等高线插值的数学模型,通过引入形状控制参数放松对曲线的光滑性的要求,增加了控制等高线形状的自由度,把 C2连续的三次B样条松弛成为 G2连续的Beta样条,实验结果表明插值的等高线符合地形综合度要求。

数字摄影测量;等高线;Beta样条曲线

等高线是一种不可或缺的图形表达方式,研究其智能化的控制过程具有极其重要的实用价值。绘制等高线是对大量离散的、又具有一定规律的几何量值或物理量值,用数学的方法插值变换成图的过程。用摄影测量方法自动采集的DEM数据[1],影像的相关误差、定向误差等对DEM数据以及从DEM插值的等高线的质量造成影响,而且自动制图中没有考虑人工绘制等高线时的“肉眼的分析和观察”规则,导致地形过度综合造成地形特征缺失,且相邻等高线形态不协调。在实际生产中,等高线的平滑、地形综合和突变点线的判断及处理等必须进行人工判断和干预,使得生成效率大大降低,因此在等高线绘制过程中引入人工绘制等高线规则,对提高等高线的质量和实际生产效率具有重要意义。

1 人工绘制等高线规则

一般等高线插值方法需要满足以下要求:①曲线应通过已知的等高线点(常称为节点);②曲线在节点处光滑,具有连续的一阶(或二阶)导数;③曲线无论挠度多大都不应自身相交;④相邻两点之间的曲线段无多余的摆动;⑤逼近实际地形的效果好,即地形综合度适宜。常用的一些插值方法都能严格满足上述的条件①和②,张力样条函数[2]插值方法,解决了曲线的多余摆动(针对条件④)。三次B样条曲线插补法是满足二阶参数连续(C2)的插值曲线[3],其每个曲线段都是以参数为变量的三次B样条函数,并非是小挠度的,而等高线曲线往往是大挠度多弯曲的曲线,因此,三次B样条曲线仅仅适合于数据点分布均匀和地形平坦地区,对条件⑤无法满足。对于条件⑤,常见的插值方法大多不能满足,这是因为等高线的绘制必须以相似的光滑曲线逼近实际地貌形态,并综合地形在一定限度内的地势起伏,使其尽可能显现出立体感,特别是大比例尺的等高线图的自动绘制,平坦地区的地形综合度明显不够,地形起伏大的地区表达也不够准确。

而绘图员以人工方式绘制的等高线总是比自动的曲线插值算法生成的曲线更合理。这是由于绘图员能凭经验捕捉到数据点所包含的几何形状信息,从而绘制出合乎要求的等高线。人从经验直觉中发现,两曲线段在连接点处有相同的切线,就认为是光滑的。按照参数连续性度量光滑度时,光滑条件必须有相同的切矢模长。而实际上,曲线具有切向连续并非必需具有连续的对一般参数的切矢,曲线具有曲率连续也不一定具有连续的对一般参数的切矢与二阶导矢。可见,参数连续是对参数曲线连接光滑度的过分限制,是人为强加的限制。

1.1 二阶几何连续

实质上,等高线的曲线形状的客观内在几何特征是不依赖于参数曲线的参数选取及具体参数化方式。基于视觉连续的几何连续性,着眼于形状内在几何特征的描述,摆脱对参数选择的依赖,为形状定义提供了额外的自由度,获得对形状控制的更大的灵活性。曲率连续但不必C2的曲线几何上连续的,称为二阶几何连续(G2)[4]。设 p(u)是 C1的曲线,p(u)关于一般参数 u的一阶导矢为 ˙p(u),且 ˙p(u)≠0,u为整数参数。Nielson[4]给出了 p(u)为 G2的条件:在 u处具有一致的关于弧长参数s的左右二阶导矢,即 p″-(s)=p″+(s),且左右二阶导矢差平行于切矢,则该 C1曲线就是 G2的曲线。设弧长参数s与一般参数u之间存在变换关系u=u(s),则其中。式(1)的几何意义如图1所示。

图1 G2的几何意义

1.2 基于人工绘制过程的等高线插值规则

为使等高线插值效果符合人类视觉,地形综合度适宜的要求,本文总结出了满足人工绘制等高线条件的插值规则:①不存在多余拐点;②曲率变化均匀;③二阶几何连续。其中,规则①和②的要求是显而易见的。规则③中的 G2连续不同于 C2连续,C2连续并不一定能保证切线方向与曲率连续,反过来,切线方向与曲率连续也不一定必须是C2连续。

2 基于人工绘制约束的等高线绘制

Beta样条具有B样条的若干性质,由于其引入了新的参量来改变曲线的形状,把C2连续的三次均匀B样条曲线松弛成为G2曲线[5],其表达式为

其中:di为控制顶点,Ni,3(u)为基函数,是由参数 u决定的三次多项式,β1和β2为形状控制参数,β1为偏移参量,β2为张力参量。对于给定的控制顶点序列{di}0n-1,Beta样条曲线的形状仅取决于基函数,形状参数β1和β2决定基函数,因此,给定一个控制多边形,Beta样条曲线的局部可通过它含有两个形状控制参数进行修改。而三次B样条曲线是一条确定的曲线,若想保持样条曲线的“次数”不变,修改该曲线的局部信息,必须移动某个顶点或插入新的控制顶点,这样必然降低曲线的可靠性。Beta样条曲线比B样条曲线更灵活、更广泛[6]。Beta样条曲线通过合适的形状控制参数实现曲线形状“细调”。绘图员在等高线绘制过程中,分析了地形的变化情况,捕捉了曲线所应包含的几何形状信息,进行了地形的综合,从而绘制出合理的等高线。那么控制曲线上各节点处形状的β1和β2参数显然不应该相同,才能够满足等高线插补条件⑤,实现绘图员人工绘制等高线的过程。因此,基于形状控制参数β1和β2约束的曲线的插值即为基于人工绘制约束的等高线插值。

2.1 沿曲线变化的形状控制参数对曲线的影响

在各节点处应当取不同的β1和β2,即形状控制参数可沿曲线变化。在某些节点处设置不同的β2和β1来修改曲线局部的信息。图2和图3为对应中间某一控制顶点的节点处,取不同的β2和β1时,该点邻近的曲线的局部变化情况。其中,图2中参数取值为β2≡0,β1分别为1、0.1和 5。图 3中参数取值为β1≡1,β2分别为0、5和10。从图中看出,某一节点处β1和β2值对曲线的影响是局部的,且β1和β2分别起着局部偏移和局部张力的作用。

2.2 满足等高线插值条件⑤的β1、β2的取值

为了使三次Beta样条曲线适应不同地形,β1和β2的取值至关重要。平坦地区的等高线上节点的曲率小,地形起伏大的区域其等高线的弯曲大,挠度大。β1的变换会引起连接点处曲线段的整体偏移,对等高线产生主导影响。β2是曲线的张力参数,表达地形综合的程度,因此对于平坦区域,节点β2值应小,相反,曲率大的节点应当紧贴控制多边形,β2尽量大。可见,β2的取值与地形变化密切相关,即与曲线的曲率变化相关。第i个节点的形状控制参数β1,i,β2,i取值为

3 实验与分析

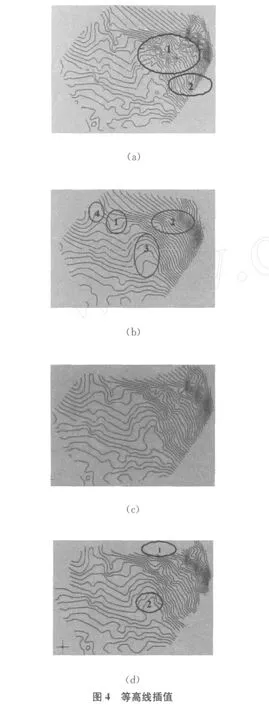
对华中地区某林地实地获取序列影像,利用多基线摄影测量系统自动生成密集三维点云,内插得到数字高程模型[7],分别利用不同的方法插补等高线。图4为各种方法插补的等高线(图4(a)、(b)和图4(c))与人工绘制的等高线(图4(d))的比较结果(等高线步距为1)。图4(a)为张力样条函数插补的等高线,其整条曲线的张力系数相同,为了表达大起伏地形,造成平坦地区2处的曲线段过于弯曲。对于如图4中1处的地形稍复杂且面积大的区域,曲线明显存在整体上弯曲大的问题,其原因是不能在每个节点处给予不同的张力系数以便适应不同地形表达的需要,一条曲线上处处相同的张力系数使得曲线段连接点处是严格的参数连续的,无法满足实现曲线内在几何形状特征表达要求的几何连续条件。张力系数为5。图4(b)为三次B样条插补的等高线,大部分曲线段,特别是1、2、3区域过于平滑,完全没有表达出地形特征,为实现其参数二阶连续,甚至在曲线段4处形成了尖角,三次B样条曲线只适合十分平坦,没有起伏变化的地形。本文的基于三次Beta样条曲线插补的等高线图4(c),由于深入分析了绘图员在实际绘图时所考虑的几何形状信息,曲线段间的连接点处根据实际地形自动调节形状控制参数,将 C2连续的三次B样条松弛成为 G2连续的Beta样条,使得同时顾及大起伏和平坦的不同地形,获得的等高线准确的表达了地形起伏变化,符合地形综合的要求,满足成图需要。图4(d)为人工绘制等高线,与三次Beta样条曲线插补的等高线曲线形态几乎完全相同。

综上所述,三次Beta样条曲线相比三次B样条和张力样条函数插补的等高线曲线更能适应起伏不同的地形的表达,这是由于Beta样条插值曲线具有β1和β2形状控制参数,而实际地形大多具有起伏变化。三次B样条插补适用于数据点分布均匀和十分平坦地形,张力样条函数插补可用于地形起伏的小面积地区,但由于每条样条上相同的张力系数,不适合实际地形的变化,不利于起伏不同的地形的表达。

4 结束语

在实际生产中,等高线的平滑、地形综合和突变点线的判断及处理等必须进行人工判断和干预,使得生成效率大大降低,而且存在一定的盲目性。本文重点分析了绘图员绘制曲线的过程,发现其能够凭经验捕捉到数据点所包含的几何形状信息,从而绘制出光滑等高线,而张力样条函数和三次B样条曲线在节点插值时,严格要求二阶参数连续,不符合人的经验直觉,是节点对参数曲线连接光滑度的过分限制。在总结了人工绘制等高线的三条规则的基础上,提出将三次Beta样条曲线作为基于人工绘制约束的等高线插值的数学模型。论述了三次Beta样条曲线的二阶几何连续性,通过引入的形状控制参数(偏移和张力形状参数)放松了对曲线的光滑性的要求,增加了控制等高线形状的自由度,从而降低了三次B样条曲线苛刻的约束要求,把 C2连续的三次B样条松弛成为G2连续的Beta样条。结果表明插值的等高线符合地形综合度要求,特别适用于起伏不同的复杂地形的表达。

[1]张祖勋,张剑清.数字摄影测量学[M].武汉:武汉大学出版社,2002.

[2]RASH ID IN IA J,MOHAMMAD IR.Tension spline app roach fo r the numerical solution of nonlinear Klein-Go rdon equation[J].Computer Physiscs Communications.2010,181(1):78-91.

[3]YANO K,HARADA K.Reconstruction of B-sp line skinning surface from generalized cylinder mesh[J].Visual Computer.2010,26(1):31-40.

[4]N IELSON G.M.Some Piecew ise Polynomial Alternatives to Splines under Tension[M].New Yo rk:Academic Press.1974.

[5]BARSKY B.A.The Beta-sp line:a local rep resentation based on shape parameters and fundamental geometric measures[D].U tah:University of U tah.1981.

[6]刘旭敏,黄厚宽,王刘强,等.带形状参数样条曲线的研究[J].计算机研究与发展,2007,44(3):487-496

[7]SHENGQ H,XIAO H.Research on Filtering of DEM Data Based on the Fisher Functions[A].2nd International Conference on Computer Engineering and Technology[C].Chengdu:IEEE.2010.

Research on contours interpolation based on Beta spline

SHENG Qing-hong
(College of Astronautics,Nanjing University of Aeronautics&Astronautics,Nanjing 210016,China)

Contour m ust be similar to the smoo th curves of app roaching the actual landscape patterns,integrated the topographic relief and dow nsof the terrain,to the extent possible to show stereo sense.Draftsmen use their experience to cap ture the geometry information contained in data to map out reasonable contour;sum up hand-draw n contours’rules;make use of cubic Beta sp line curve interpolation contours;introduce migration and tension shape Parameters to release the requirement to the smooth curves,reducing cubic B spline harsh requirements,making the consecutive cubic B sp line to flab G2 consecutive Beta sp line,to p roduce the reasonable requirements of the Comp rehensive contour map,and eventually realize the measurement hillside woodland of images from the ground.

digital photogrammetry;contours;Beta sp line

TP317.4

A

1006-7949(2010)06-0024-04

2010-09-11

盛庆红(1978-),女,讲师,博士.

[责任编辑张德福]