基于相位差分的 GPS/GLONASS组合定位算法研究

孙洪瑞,沈云中,周泽波,虞祖培

(1.中交第三航务工程勘察设计院有限公司,上海 200032;2.同济大学 测量与国土信息工程系,上海 200092;3.电子科技大学空天技术研究院,四川 成都 610054)

基于相位差分的 GPS/GLONASS组合定位算法研究

孙洪瑞1,沈云中2,周泽波3,虞祖培1

(1.中交第三航务工程勘察设计院有限公司,上海 200032;2.同济大学 测量与国土信息工程系,上海 200092;3.电子科技大学空天技术研究院,四川 成都 610054)

针对短基线详细研究 GPS/GLONASS组合定位函数模型,引入一种简单易行的模糊度求解方法以正确固定 GLONASS模糊度,最后笔者自编软件实现基于相位差分的 GPS/GLONASS高精度组合定位,并采用实际数据验证其正确性和有效性。结果表明:GPS/GLONASS组合系统优于单系统,采用相位观测值可获得高精度定位结果。

GPS;GLONASS;相位差分;组合定位

全球导航卫星系统(GLO bal’naya NA vigatsionnaya S putnikovaya S istema or GLO bal NA vigation S atellite S ystem,简称 GLONASS)是前苏联(现俄罗斯)于1976年开始建立的第二个全球卫星定位系统。由于受俄罗斯经济衰退的影响,GLONASS卫星缺乏有效的维护和更新,以至于到2001年时只有7颗卫星可用,于2001年8月启动 GLONASS的恢复和更新计划。目前 GLONASS可用卫星已达17颗(见图1),预计于2010年完成星座的24颗布设。此外,俄罗斯已经决定将星座的卫星数目增至30颗,并增加CDMA信号,以便与 GPS、GAL ILEO进行组合定位。与 GPS不同,GLONASS采用频分多址(Frequency Division M ultip le Address,FDMA)的方式识别卫星信号。GLONASS卫星也是利用两个L波段频率发射载波无线电信号,即L 1和L 2载波,相应的频率分别为 fL1=(2 828+K)×0.562 5 M Hz和 fL2=(282 8+K)×0.437 5 M Hz,K=-7～6。同一颗卫星的两个频率之间满足fL1/fL2=9/7的关系(GPS的两个频率满足 fL1/fL2=77/60)。GLONASS卫星上的载波也调制了两种伪随机噪声码:S码(即 GPS的C/A码)和 P码。此外,俄罗斯对 GLONASS系统采用了军民合用、不加密的开放政策,即普通用户均可同时使用 P1、P2和L1、L 2民用信号。GLONASS与 GPS系统的差异具体可参见文献[1-2]。

采用GPS/GLONASS组合定位主要有以下优点:①能选择几何配置更好的卫星定位,提高定位精度;②减少卫星信号被遮挡而引起的卫星不足的影响,特别是多山或城市地区;③使用多颗卫星,多余的观测增加了定位的可靠性(见图2);④使用多卫星导航系统,就会削弱对单一系统的依赖性;⑤可及时识别和停用故障卫星;此外,可有效地减弱美国限制性政策的影响(如实施 SA、AS政策),提高卫星导航定位的可用性、可靠性、精确性及系统的自主完备性监测(RA IM)能力。

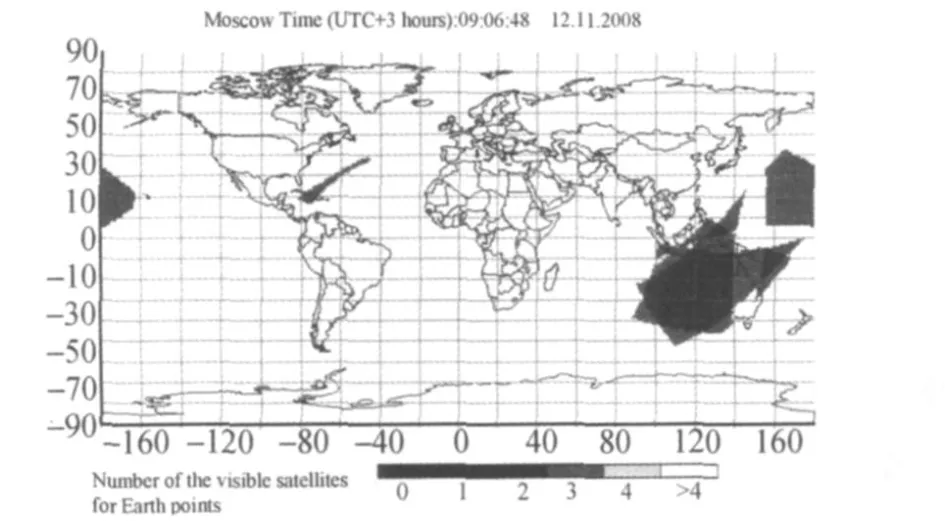
图1 GLONASS星座当前的卫星可见数目

图2 某IGS站 GPS/GLONASS卫星分布图

组合定位是卫星定位未来的重要发展方向。国外已经开发出相应的软、硬件产品,而且已经有一定的研究成果,但并不公开其具体的、实际性的技术细节,只是给出结果及必要的介绍[3]。为此,本文针对短基线首先详细研究了 GPS/GLONASS组合定位函数模型,并引入了一种简单易行的模糊度求解方法以正确固定 GLONASS模糊度。最后笔者采用自编软件实现了基于相位差分的 GPS/GLONASS高精度组合定位算法,并采用实际算例验证了本文算法的正确性和有效性。

1 GLONASS函数模型

GLONASS的观测方程模型与 GPS类似,但在系统的参考时间、卫星发射频率与识别方式等方面有所差异,则其伪距与相位的非差观测方程为[4]

式中 :Pik,φik分别表示测站k至卫星i的伪距和相位(单位:周)观测值,ρik表示卫地真实的几何距离,c表示光速,d ti为卫星钟差,d Tk表示接收机钟差,ηik表示与卫星和接收机相关的硬件延迟,doirb、dtirop、diiono、dmiult分别表示卫星轨道误差,对流层延迟、电离层延迟、多路径效应,εP与εφ分别为码和相位噪声。相应地,站间单差的观测方程可写为

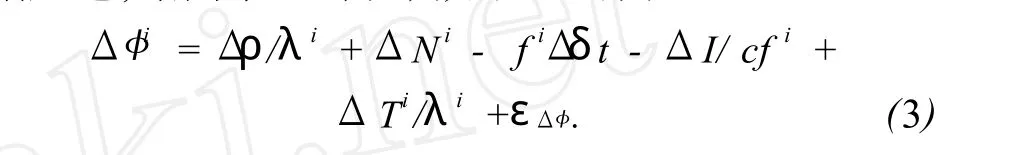
在此基础上继续一次星间差分,GLONASS双差观测方程可表示为

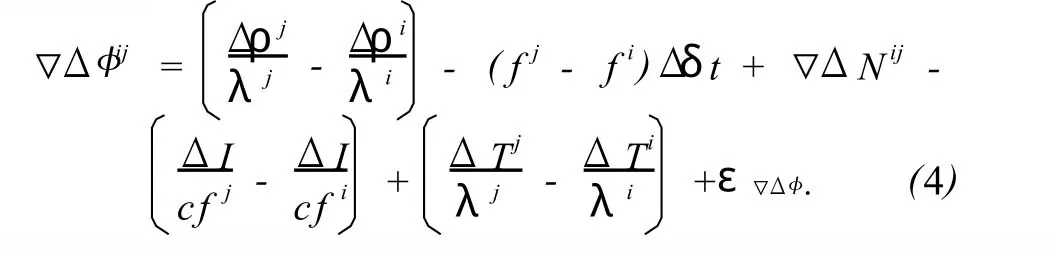
由于差分不仅消除了卫星钟差与接收机钟差的影响,还大大削弱了电离层延迟与对流层延迟的影响。下文主要研究采用差分模式进行 GPS/GLONASS组合差分定位解算。

2 GPS/GLONASS整周模糊度解算

由于GLONASS卫星采用频分多址的方式识别,不同卫星间的载波相位频率不同,其双差模糊度参数不具有整周特性,必须采取一定的变换才可以求解双差模糊度的整周解,故 GLONASS模糊度的处理方法较 GPS更为复杂。目前国内外关于GLONASS模糊度分解的算法也有不少[5-8]。模糊度的正确求解是获得高精度 GPS/GLONASS基线向量解的先决条件和关键问题。模糊度的正确求解取决于观测值的质量和卫星的数量与分布。载波相位信息是时间的函数,与卫星的运动直接相关,即使在良好的观测条件下,时间也是模糊度求解成功与否的关键因素。模糊度搜索方法有很多,比如:最小二乘搜索法、快速模糊度分解法、模糊度函数法,LAMBDA方法以及ARCE算法等[9],其中以去相关技术为核心的LAMBDA方法最为经典。本文主要参考韩绍伟博士于1999年提出的算法进行短基线的 GLONASS模糊度解算方法[8],结合LAMBDA以正确固定GPS整周模糊度。

1)采用 GPS/GLONASS伪距观测方程(5)、(6)计算接收机钟差参数。

其中,GPS采用伪距观测双差观测方程,GLONASS采用伪距单差观测方程,它们主要用来解算接收机钟差单差Δδt。值得注意的是,接收机钟差参数必须每个历元解算一个。

2)利用 GLONASS单差相位观测方程探测GLONASS基准星周跳。需要指出,GLONASS单差相位观测方程基准星i周跳无需对其修复。

3)GPS/GLONASS双差相位观测方程用来求解模糊度并解算测站近似坐标。

综合式(5)、(6)与式(10)解算 GLONASS双差模糊度,但是不能用其解算测站精确坐标,否则误差较大[8]。因为采用上式求解模糊度过程中,一部分会被位置参数所吸收,从而导致此时位置参数精度偏低[3]。

4)采用式(11)(单位:m)以精确解算测站位置参数。

对上式求解时,需将基准星 i的单差模糊度ΔNi视为待估参数。

特别地,对于短基线而言,忽略电离层和对流层延迟的影响以后,式(10)、(11)可简化为式(12)、(13),模型变得更加简单而准确。

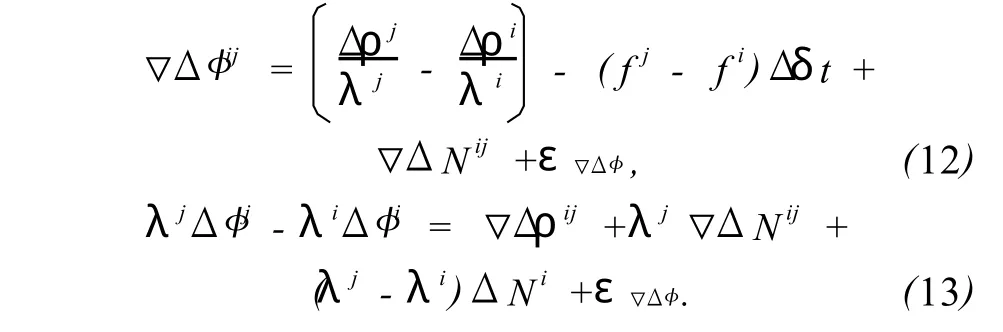
3 GPS/GLONASS整周模糊度解算流程

可将 GPS/GLONASS模糊度解算归纳为以下3个步骤,流程如图3所示。

1)利用 GPS/GLONASS伪距观测方程式(5)和(6)得到两个接收机钟差之差Δδt和测站的近似坐标;

2)将Δδt代入式(10)或式 (12),用 LAMBDA方法解算双差模糊度▽ΔN;

3)当 GLONASS基准星无周跳或者已经探测修复之后,将▽ΔN代入式(11)或式(13)解算 GLONASS参考星的单差模糊度ΔNi和测站精确坐标。

图3 GLONASS模糊度解算流程

4 算例分析

为了验证本文提出方法的正确性和有效性,笔者根据上述理论自编软件对实测数据进行了高精度精密定位解算。实验数据来源于2008-03-20在同济大学校园内静态观测的一条超短基线数据,基线相关信息如表1所示。

表1 实验所用基线的相关信息

将整个观测数据分成9个时段(每时段历元数为100)。其间保持同步锁定4颗 GLONASS卫星和8颗 GPS卫星,共计12颗可用卫星。相位解算结果如图4所示。

图4 GPS、GLONASS以及 GPS/GLONASS相位差分定位结果比较

由图4可知,GPS相位差分定位精度均在1 cm以内,可达到毫米级的高精度定位;GLONASS相位差分定位的精度在4 cm以内,有些时段的精度可达毫米级,较 GPS定位精度低,影响 GLONASS定位精度的主要因素是 GLONASS卫星之间的硬件延迟项无法消除,此外也跟 GLONASS卫星个数较少、图形强度较弱有关。而 GPS/GLONASS组合定位的结果与 GPS单系统定位结果基本相当,但其稳定性和可靠性较 GPS均有所提高[10-12]。图5为本文GPS/GLONASS相位差分定位的程序设计模块示意图。

图5 GPS/GLONASS相位差分定位程序设计

5 结束语

本文针对短基线详细研究了 GPS/GLONASS组合定位函数模型,引入了一种简单易行的模糊度求解方法以正确固定 GLONASS模糊度,最后笔者自编软件实现了基于相位差分的 GPS/GLONASS高精度组合定位,并采用实际数据验证了其正确性和有效性。结果表明:①GLONASS相位差分定位的精度低于 GPS,其原因可能是受硬件延迟项的影响,具体尚待更进一步的研究;②GPS/GLONASS组合系统优于单系统,采用相位观测值可获得高精度定位结果。

[1]孙洪瑞,沈云中,周泽波.GPS/GLONASS组合点定位模型及其精度分析[J].测绘工程,2009,18(1):8-10.

[2]高星伟,葛茂荣.GPS/GLONASS单点定位的数据处理[J].测绘通报,1999(4):8-9.

[3]高星伟.GPS/GLONASS数据处理方法研究及软件编制[D].北京:中国测绘科学研究院,1999.

[4]ROSSBACH U.Positioning and navigation using the Russian satellite system GLONASS:[Ph.D Dissertation].Germany:University of M unich,2000.

[5]ALFRED LEICK.Aspects of GLONASS carrier-phase differencing.GPS Solution,1998,2(1):36-41.

[6]JWANG.An app roach to GLONASS ambiguity resolution[J].Journal of Geodesy,2000(74):421-430.

[7]JWANG,C RIZOS,M P STEWART,et al.GPS and GLONASS Integration:Modeling and Ambiguity Resolution Issues[J].GPS Solution,2001(5):55-64.

[8]S HAN,L W DA I,CHRIS RIZOS.A new data p rocessing strategy for combined GPS/GLONASS carrier phase-based positioning[J].12th Int.Tech.Meeting of the Satellite Division of the U.S.Inst.of Navigation,Nashville,Tennessee,1999:1619-1627

[9]李博峰,沈云中.附有约束条件的 GPS模糊度快速解算[J].武汉大学学报:信息科学版,2009,34(1):117-120.

[10]高星伟,李毓麟,葛茂荣.GPS/GLONASS相位差分的数据处理方法[J].测绘科学,2004,29(2):22-24.

[11]CARINEBRU YN INX.Comparing GPS-only w ith GPS+GLONASS positioning in a regional permanent GNSS network[J].GPS Solution,2007,11:97-106.

[12]CEFALO RAFFAELA,GA TTIMARCO.Dual frequency GPS+GLONASSmeasurement in the static relative position[J].2000,59:391-403.

Research on GPS/GLONASS integrated positioning algorithm based on different carrier-phase

SUN Hong-rui1,SHEN Yun-zhong2,ZHOU Ze-bo3,YU Zu-pei1
(1.CCCC.Third Harbo r Consultants Co.,L td,Shanghai200032,China;2.Dep t.of Survey and State Land Information Engineering,Tongji University,Shanghai 200092,China;3.Institute of Astronautics&Aeronautics,UESTC,Chengdu 610054,China)

The paper detailedly investigated the functional model of GPS/GLONASS for short baselines.Then a simp le and p racticed method for GLONASS ambiguity resolution was introduced.Finally,the GPS/GLONASS integration positioning p rogram was realized w ith MA TLAB language and its efficiency was validated w ith real data.The result show s that GPS/GLONASS integration system is superior to single system and can achieve the high accuracy of positioning w ith carrier-phase measurement.

GPS;GLONASS;differenced carrier-phase;integrated positioning

P228.4

A

1006-7949(2010)06-0020-04

2009-12-30

孙洪瑞(1984-),男,助理工程师,硕士.

[责任编辑刘文霞]