三维卷曲结构真丝新材料的拉伸性能建模研究

王 琦，林 红，陈宇岳，田立勇

(苏州大学 纺织与服装工程学院，江苏 苏州 215021)

三维卷曲结构真丝新材料的拉伸性能建模研究

王 琦，林 红，陈宇岳，田立勇

(苏州大学 纺织与服装工程学院，江苏 苏州 215021)

提出由Maxwell元件、线性弹簧和非线性弹簧组成的四元件非线性黏弹模型，对具有三维卷曲结构真丝新材料的拉伸性能进行测试和分析，结果表明，理论预期与试验结果相符。

弹力真丝；三维卷曲；非线性黏弹模型；断裂强力

具有三维卷曲结构的真丝新材料是通过物理和化学作用处理后得到的全真丝弹力真丝，三维卷曲结构真丝新材料是利用桑蚕丝分子经膨化药液处理改变蚕丝纤维的超分子结构，使其形成显著的卷曲特征，其代表性的产品有膨体弹力真丝和柞桑弹力真丝。三维卷曲结构真丝新材料的特点是丝身具有明显的膨松性、弹性与良好的复原性[1]。在松弛状态下，丝身有空间螺旋圈，呈三维状，具有很强的毛型感；在拉伸作用消失后，丝身会自然恢复到原来的形状，具有良好的形状记忆功能。与普通桑蚕丝的明显区别在于弹性和膨松性显著增加，丝身更加柔软[2-3]。

力学模型能直观、形象地描述纺织材料的宏观力学行为,并可对其力学性质进行定量分析[4-5]。本研究对具有三维卷曲结构真丝新材料的力学性能变化规律进行系统分析，建立三维卷曲真丝新材料的拉伸力学模型，并根据四元件模型对其应力-应变曲线进行拟合，将理论值与实测结果相比较，验证模型的正确性，为三维卷曲真丝新材料的后加工提供相关的理论数据与指导。

1 三维卷曲结构真丝新材料力学模型的建立

采用Hearle法[6]确定三维卷曲真丝新材料有代表性的拉伸应力-应变曲线图(图1)，可知纤维拉伸曲线呈现反S形，并且在起始阶段呈线性关系，但在断裂过程中，由于产生较大的变形，从最初的弹性变形到塑性变形再到破坏性变形，材料具有明显的非线性。

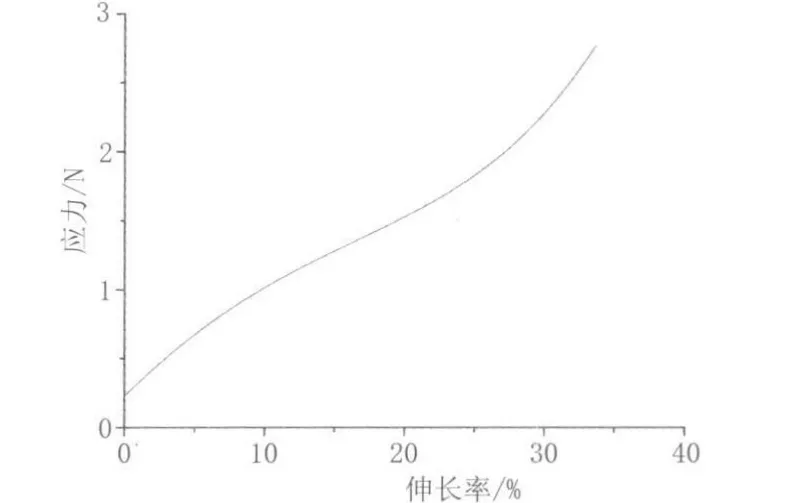
图1 三维卷曲结构真丝拉伸曲线Fig.1 Three-dimensional Crimp Silk Tensile Curve

对三维卷曲真丝新材料的代表性拉伸曲线分析表

明：由于预加张力的存在，伸长等于零时曲线与强力轴相交，交点的纵坐标等于预加张力，曲线的初始部分斜率较大，随着纱线伸长的增大，强力缓慢增加，在接近断裂时，强力随伸长的增大而快速增大，模型方程中有常数项、线性成分和非线性成分。因此力学模型中应该含有能反映线性力学性质的虎克弹簧，以及反映非线性部分的非线性元件等。确定采用的力学模型如图2所示。

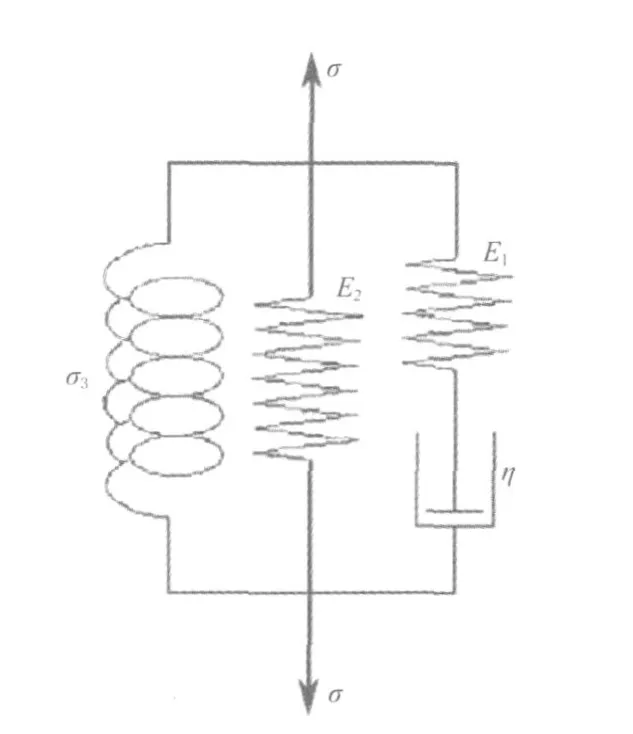
图2 三维卷曲结构真丝力学模型Fig.2 Mechanical Model of Three-dimensional Crimp Silk

该模型是由Maxwell单元并联一个线性弹簧再并联一个非线性弹簧构成。Maxwell元件中弹簧的弹性模量设为E1，线性弹簧的弹性模量为E2，牛顿黏壶的阻尼系数为η，假定Maxwell元件、线性弹簧和非线性弹簧受到的应力为σ1、σ2、σ3。产生的应变为ε1、ε2、ε3，且σ＝σ1＋σ2＋σ3，ε1＝ε2＝ε3。在模型中的Maxwell元件[7]：

线性弹簧应力-应变关系符合胡克定律，即：

对于非线性弹簧产生的应力-应变的关系为：

认为纱线的拉伸为等速拉伸，则有ε＝kt，k为常数。

联立式(1)(2)(3)推导出模型应力-应变曲线方程为：

在试验中施加了一定的预张力，在本次试验中预加张力σ0＝30 cN，故将式(4)修正为：

为了计算方便，假设E2＝A，b＝B，kη＝C，E1/kη＝D，则：

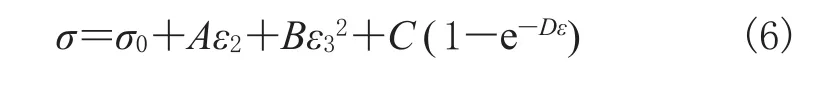
将式(7)代入式(6)可得[8]：

进一步整理得：

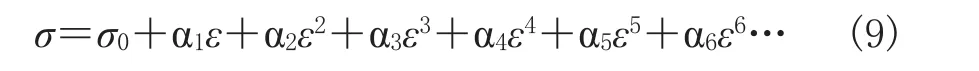
2 试验材料与方法

选取三维卷曲结构真丝新材料和普通真丝为试验用材料。两者平衡24 h后，在INSTRON 3365万能材料试验机上进行拉伸试验，试样纤度30 tex，试样长度250 mm，拉伸速度250 mm/min，预加张力0.1 cN/dtex，试验次数100次，试验温度20 ℃，相对湿度65 %。

3 结果与讨论

3.1 三维卷曲结构真丝与普通真丝力学性能比较

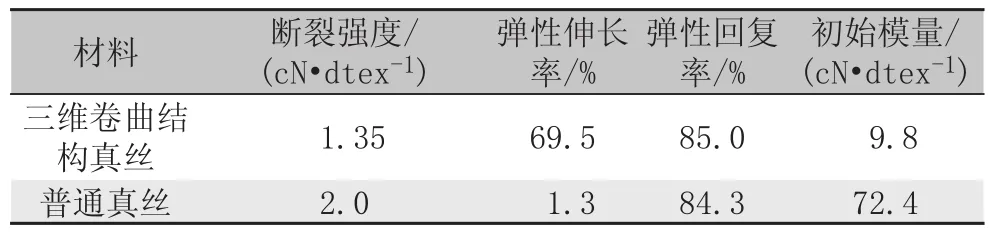
表1 三维卷曲结构真丝与普通真丝的力学性能Tab.1 Three-dimensional Crimp Silk and Common Silk Mechanical Properties

3.2 三维卷曲结构真丝拉伸曲线拟合

选取断裂强力、断裂伸长率、初始模量最接近平均值的拉伸曲线作为三维卷曲真丝的代表性拉伸曲线，利用Matlab数学软件[9-11]，采用最小二乘法，根据式(9)拟合出具有三维卷曲结构真丝新材料的拉伸曲线方程并计算理论曲线。任取6组试验数据代入式(9)即可求出拟合参数(表2)。

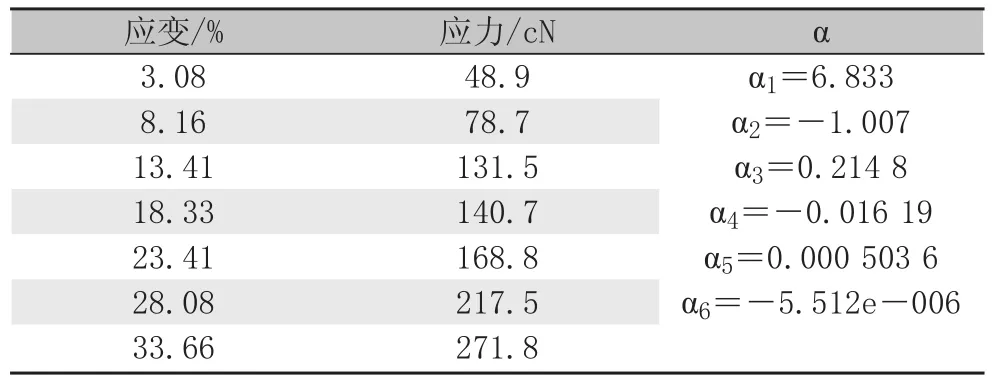
表2 拟合参数Tab.2 Fitting Parameters

模型中相关系数R2＝0.997 3。

由拟合参数得到的拟合拉伸曲线如图3所示，实线为拟合曲线，“·”为实测数据。

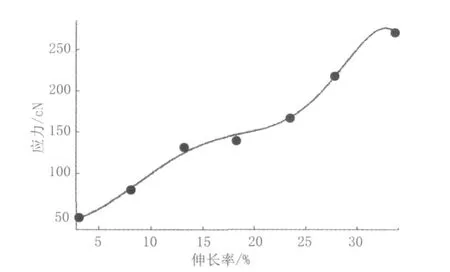
图3 三维卷曲结构真丝新材料拟合拉伸曲线与实测数据Fig.3 Three-dimensional Crimp Silk Fitting Tensile Curve and Measured Data

由拟合拉伸曲线可以看出，该曲线成反S形，可分为线性区、屈服区、强化区。在线性区三维卷曲真丝新材料变形的大小正比于外力的大小，服从虎克定律，当外力除去后，材料的变形将回复到原来的位置，是完全弹性回复属于急弹性形变。当外力增大时材料进入屈服区，材料伸长变得容易，而应力上升很缓慢，此时应力-应变曲线的斜率较小。当外力继续增大时，即进入强化区，分子链充分伸直，进一步拉伸分子链较困难，应力应变曲线斜率增大，直至材料拉伸到断裂。通过模型计算的数据与实测数据基本相符，实测数据点基本上都在理论拉伸曲线上，由此可以说明本研究建立的理论模型可以预测真丝新材料的拉伸性能。

4 结 语

由Maxwell、牛顿黏壶等组成的四元件模型能很好地模拟具有三维卷曲结构真丝新材料的拉伸力学性能，可以根据模型预测该材料的拉伸特性，为以后三维卷曲真丝新材料的后加工提供相关的理论数据与指导。

[1]林红.柞桑弹力真丝的性能研究[J].丝绸，1999(7)：15-17.

[2]陈宇岳.柞蚕丝与桑蚕丝的形态差别化特性研究[J].苏州丝绸工学院学报，2000(4)：21-27.

[3]陈宇岳，盛家镛，谢佳，等.膨体弹力真丝的形态结构研究[J].纺织学报，1999(6)：6-8.

[4]崔世忠，石风俊.大豆蛋白质纱拉伸性质建模的研究[J].纺织学报，2003，24(4)：44-46.

[5]杨英贤，石风俊. 牛奶丝纤维拉伸性能建模的研究[J].合成纤维，2005，34(7)：24-26.

[6]于伟东，储才元.纺织物理[M].上海：东华大学出版社，2009.

[7]张洪弟，骆呈军.三元件模型理论及其在纺织上的应用[J].北京纺织，2004，25(2)：57-59.

[8]刘元鹏，杨庆斌，谭震，等.牛奶纤维的力学性能及模拟分析[J].青岛大学学报：工程技术版，2008，23(1)：13-17.

[9]许波，刘征.MATLAB工程数学应用[M].北京：清华大学出版社，2000.

[10]何仁斌. MATLAB工程计算及应用[M]. 重庆：重庆大学出版社，2001.

[11]许国根，许萍萍.化学化工中的数学方法及MATLAB实现[M].北京：化学工业出版社，2008.

Research on Model for Mechanical Properties of New Silk Material with Three-Dimensional Crimp Structure

WANG Qi, LIN Hong, CHEN Yu-yue, TIAN Li-Yong

(College of Textile and Clothing Engineering, Soochow University, Suzhou 215021, China)

A four parameter non-linear viscoelastic model is put forward, which is consisted of the Maxwell element, linear spring and nonlinear spring. The tensile properties of three-dimensional crimp silk are tested and analyzed. The result shows that: theoretical expectations and experimental results can be consistent.

Elasticity silk; Three-dimensional crimp; Nonlinear viscoelastic model; Breaking strength

TS101.2；TS102.33

A

1001-7003(2010)12-0019-03

2010-09-13；

2010-10-29

国家教育部博士点基金项目(200602850004)；江苏省高校重大基础研究项目(08KJA540001)

王琦(1986－ )，男，硕士研究生，研究方向为纤维材料的研究和开发。通讯作者：陈宇岳，教授，博导，chenyy@suda.edu.cn。