横向受载空心桩动力性能研究
2010-11-14张永谋
张永谋,杨 敏
(1.兰州交通大学土木工程学院,甘肃兰州730070;2.同济大学地下建筑与工程系,上海200092)
0 引言
我国采用的计算推力桩的现行方法,如张有龄法、m法、c法等,都是单一参数法[1~4],即在幂函数土抗力模数K=mxq中,q预先确定,只有一个待定参数m值的方法。用单一参数法计算推力桩,有一个共同的缺点,即桩在地面处的挠度、转角、桩身最大弯矩及其所在的位置等,不能同时很好地符合实测值,只能凑合到较为接近的程度。其原因是待定参数的数目不够,或选择得不恰当所致。但是,对桩基础的设计至关重要,是值得十分重视的问题。解决问题的途径之一是增加参数,并且要求参数选择得恰当。综合刚度原理和双参数法,用于推力桩的非线性分析和动响应分析,能取得比较满意的效果。
1 无量纲差分方程式的推导
将桩身划分为n个单元,则共有n+1个划分点。要这n+1个点上都能建立差分方程式,则在桩轴两端延伸线上分别设两个点[5,8]。因此,最后得到桩身划分点的编号如图1所示。
现在,桩身的划分点为n+1个,再加上桩顶以上和桩底以下各两个虚拟点,则共有n+5个未知侧移需要求解,但只有n+1个方程,所以需要根据桩底和桩顶处的边界条件得出另外四个附加方程,连同上述n+1个方程,刚好联立求解这n+5个点侧移值。
根据有限差分法,得到桩身各节点位移函数:
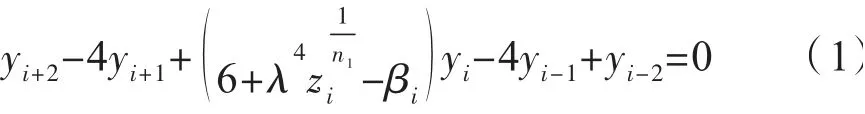


式(2)即为桩身位移的递推公式,它可用于桩身第i=3,4,…,n+3等点,得到n+1个方程,再加上4个边界条件,共计n+5个方程,解这组n+5元联立方程,就可以得出包括虚拟点在内的n+5个节点的位移yi,进而可以通过各阶中心差分式求出各个节点的转角和内力。
2 试验桩实例计算
一桩基水平激振试验如图2所示,实验在砂坑中进行,桩为150 cm长的钢管,土砾砂,承台为钢筋混凝土,桩、土、承台的基本资料见表1所列。
共振时频率f=9.4 Hz,
地面处水平位移的模为|y0|=0.068 08 cm,
转角的模为|φ0|=0.002 36 rad,
弯矩的模为|M0|=5.88 kN·cm,


表1 桩、土、承台基本资料汇总表
剪力的模为|Q0|=0.347 kN。
用前述方法,取1/n=0.75,α=0.043 63 cm-1,综合刚度EI=2.0202×108N·cm2时,
令Ωy=0,则从式(84)就得到车轮不旋转时环向指数为m的固有频率和振型。车轮旋转时,有离心效应(由离心矩阵Mc描述)和陀螺效应(由陀螺矩阵G描述),它们(尤其是陀螺矩阵G)的存在使得不旋转车轮的一个固有频率变成旋转车轮的2个特征频率。

2.1 系数计算
代入已知参数可求得各方程的系数。
2.2 列方程计算挠度
用递推公式:
yi+2-4yi+1+ (6+ Ai)yi-4yi-1+yi-2=0可写出16个方程。
用地面处桩头边界条件可写出两个方程,即:

用桩底边界条件可写出两个方程,即:

联立解线性方程组。
方程形式如:
AY=B


其中:用克拉默法则解此线性方程组,可解得挠度yi,用于后续计算。
2.3 转角计算

2.4 弯矩计算

2.5 剪力计算

2.6 土抗力集度计算

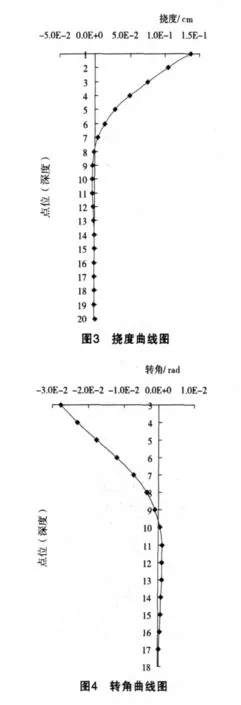
2.7 计算结果(见图3~7)
3 实心桩与空心桩的对比
地质条件:0~14 m,中砂、中密、饱和;14~17 m,粗砂、中密、饱和;17~21 m,砂质粘土、密实、半坚硬。
荷载及比值:桩在地面处所受的动力矩幅值M0和横向动力幅值Q0之比e=M0/Q0=0.25 m,其中Q0=60×104N。

表2 桩身弯矩与挠度的实测值和计算值汇总表

计算条件:1/n=0.5,m1=4.347 726 6 N·cm-3.5。
桩的物理几何特征:
桩1:钻孔灌注混凝土实心桩,桩径D=1.62 m,桩的入土长度h=18.8 m,混凝土密度ρ=2.4×10-3kg/cm3,混凝土弹性模量Ep=3.0×106N/cm2,有钢筋骨架。
桩2:钻孔灌注混凝土空心桩,桩外径D=1.62 m,桩内径d=1.02 m,桩的入土长度h=18.8 m,混凝土密度ρ=2.4×10-3kg/cm3,混凝土弹性模量Ep=3.0×106N/cm2,有钢筋骨架。

桩3:钻孔灌注混凝土空心桩,桩外径D=2.22 m,桩内径d=1.52 m,桩的入土长度h=18.8 m,混凝土密度ρ=2.4×10-3kg/cm3,混凝土弹性模量Ep=3.0×106N/cm2,有钢筋骨架。即,桩1桩身截面面积与桩3桩身截面面积相等,桩1实心桩面积为:2.060 15 m2,桩3空心桩面积为:2.055 13 m2。如图8所示,桩1和桩3阴影部分面积相等。

计算参数见表3所列。

表3 计算参数表
图9~13列出了桩1、桩2和桩3的挠度、转角、弯矩、剪力和土抗力的对比曲线。
4 结论

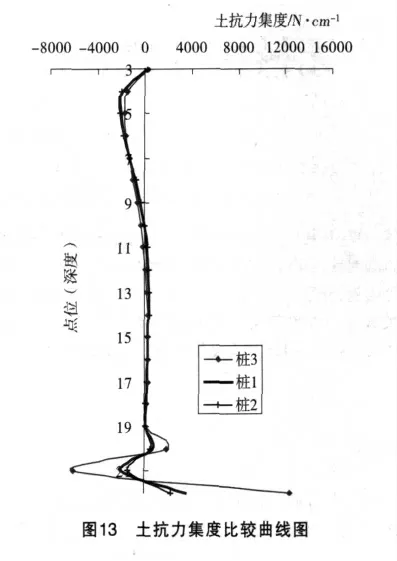
该设计使用了等效悬臂法估算推力桩的固有频率,之后,采用吴恒立提出的综合刚度原理和双参数法,计算共振时桩在地面处的挠度和转角幅值,以及桩身最大弯矩的幅值及其发生的位置。选择恰当的参数,分别计算了实心桩和相等外径的空心桩及与实心桩有相同等效截面积的空心桩在横向动荷载作用下桩在任意截面的挠度、转角、弯矩、剪力和土抗力集度。并对计算结果进行了对比分析(挠度曲线、转角曲线、弯矩曲线、剪力曲线、土抗力集度曲线),得出以下结论:
(1)外径相同的实心桩与空心桩相比,实心桩各截面的挠度和转角较空心桩的小。
(2)外径相同的实心桩与空心桩相比,实心桩各截面所受弯矩和剪力较空心桩的大。
(3)有效截面积相等的实心桩和空心桩相比,实心桩地面处的挠度和转角几乎是空心桩的2倍。
(4)有效截面积相等的实心桩和空心桩相比,实心桩各截面所受弯矩和剪力比空心桩的大且随桩在土中的深度衰减较慢。
[1]胡人礼. 桥梁桩基础分析和设计[M]. 北京:铁道出版社,1987.
[2]赵明化. 桥梁地基与基础[M]. 北京:人民交通出版社,2004.
[3]横山幸满. 桩结构物的计算方法和计算实例[M]. 北京:中国交通出版社,1984.
[4]卢世深,林亚超. 桩基础的计算和分析[M]. 北京:人民交通出版社,1987.
[5]吴恒立. 计算推力桩的综合刚度原理和双参数法(第二版)[M].北京:人民交通出版社,2000.
[6]陈仲颐,周景星,王洪瑾. 土力学[M]. 北京:清华大学出版社,1994.
[7]戴自航,沈蒲生. 推力桩计算的综合刚度双参数法半数值解[J].福州大学学报,2004,32(6):741-746.
[8]蔡婧,吴恒立. 推力桩动力响应的计算[J]. 工程力学,1999,3(a03):741-746.
