Budaiwi模型的修正及实验验证

郭兴国,陈友明,邓永强,张 乐

(湖南大学a.土木工程学院;b.教育部建筑安全与节能重点实验室,长沙 410082）

在中国南方地区,墙体的热湿迁移对围护结构的热工性能、建筑能耗和室内环境有着十分重要的影响[1]。墙体湿传递过程直接影响着室内湿度水平和潜热负荷。同时,湿传递还有可能引起墙体内部湿积累,导致保温材料保温性能下降,增加墙体的传热系数,进而增加建筑能耗。湿积累还会导致建筑物在使用几年后便出现墙表面剥蚀、渗漏、发霉甚至结构出现损坏的现象,这严重影响了墙体的使用寿命和美观。因此,为了提高建筑能源利用率和结构工程的耐久性、改善人居环境,深入研究建筑构件内热湿耦合迁移情况是十分重要的。

国外从20世纪70年代后期开始重视对热湿环境下墙体内湿迁移过程的理论及应用研究,发展了许多围护结构热湿传递的数值模型。其中被广泛采用的是Philip和DeVries模型[2],该模型参数的物理意义比较直观明了,但是对于多层墙体而言,由于所采用的湿驱动势在层与层之间的交界面处不连续,需要重复计算。为了解决此不连续问题,一些学者对该模型进行了一些改进[3-5]。另外一个被广泛采用的是Luikov模型[6],该模型比较全面的描述了墙体内的热湿迁移情况,但是解法非常复杂,而且一些参数很难确定。Qin在该模型的基础上建立了一个多层材料内的热湿耦合传递方程[7-9]。

在实际建筑应用中,一些学者通过各种假设建立了一些简化模型[10-13]。较为系统的研究了复合墙体传热传湿特性的是Budaiwi等人,他们建立了评价复合墙体瞬态热湿的动力学模型[14]。各种湿工况下的湿过程和墙体各层的含湿量都能被较为准确的估算。但是该模型在传质控制方程中有遗漏之处,边界条件较为简单,忽略了太阳辐射的影响,这将导致计算误差增大,而且该模型没有用在实际气候条件下墙体的实测数据进行验证。

鉴于此,该文在Budaiwi模型的基础之上,以墙体内的空气含湿率和温度为驱动势,将空气含湿率看做是材料含湿量和温度的函数,对该模型进行了修正。为了验证模型的准确性,建立多层墙体热湿耦合传递试验测试装置,进行了试验研究。

1 模型的修正

根据文献[14]的研究,墙体内的湿传递过程为:

根据下列表达式即可求出方程中各偏导:

将各偏导数代入方程(1)即可得质传递方程为:

相关边界条件为:

将此质传递方程与文献[14]的质传递方程进行比较可见,Budaiwi模型在质传递方程中漏掉了,这将导致较大的误差特别是忽略了ρm。

热传递过程方程为[15]:

相关边界条件为:

式中,K为导热系数,W/m·K;hc为表面换热系数,W/m2·K;hfg为蒸发潜热,J/kg;cvm为材料比热,J/kg·K;ρm为材料密度,kg/m3;Qrad为太阳辐射得热。

在墙体的内表面处,Qrad=0,外表面处的太阳辐射得热可根据文献[16]计算得出。将此能量守恒方程与Budaiwi模型中的能量守恒方程进行比较可见,在由于相变引起的能量变化项中Budaiwi忽略了比例系数。同时,Budaiwi还忽略了边界处太阳辐射的影响,实际上太阳辐射的影响要比相变热的影响大的多,特别是在外表面。

采用有限差分法来解此控制方程,为了确保数值稳定性,采用隐式格式。离散方程用Gauss-Jordan消元法求解。为了评估墙体内部冷凝情况,在每一个时间步长,每个节点的空气含湿率都跟对应该节点温度的饱和空气含湿率进行对比,如计算值大于饱和空气含湿率,则表示该处有冷凝发生,将该点的空气含湿率设为饱和空气含湿率。

2 实验测试方法

为了验证模型的正确性,在湖南大学暖通试验楼顶楼进行了试验测试,并将测试结果与试验测试结果进行对比。实验墙体(500 mm×500 mm)构造方式及传感器安装如图1所示,墙体共3层:外墙为20 mm水泥砂浆层,中间为240 mm厚红砖墙,内层为20 mm水泥抹灰层。墙体四周用300 mm厚XPS挤塑式聚苯乙烯隔热保温板进行绝热隔湿。在墙体内部的分界面处安装温度传感器(Pt100)和相对湿度传感器(HIH-4000)来测试该处的温度和相对湿度,靠近墙体表面的环境温湿度用温湿度传感器测试,所有传感器都安装在试验墙体的中心位置。所有传感器都事先进行了标定,在埋入墙体之前,分别用冰水混合物和饱和氯化钠溶液对温度传感器和相对湿度传感器进行了校正。温度传感器的测量误差为:±(0.15+0.002|T|),相对湿度传感器的测量误差为±3.5%。所有传感器都在砌墙体时埋入。太阳辐射仪放置在离墙较远的空旷处测量总辐射得热量。试验数据用型号为EN880的数据采集仪每隔半小时采集一次。图2为试验装置照片。实验测试时间为1个月。

图1 墙体结构及传感器安装示意图

图2 试验图片

3 模型的解与实验验证

计算时假设墙体内各点的初始温湿度都相同,其值由试验条件决定。温度为23℃,相对湿度为60%。材料的物性参数(如表1所示)来源于文献[17-18]。墙体内外表面的热交换系数分别取8.72 W/m2·℃和23.26 W/m2·℃,质交换系数可根据热交换系数值由Lewis关系式求得(Lewis数等于1)。外表面的太阳辐射得热取为垂直壁面的太阳直接辐射得热量,其值可根据测试得到的水平总辐射得热利用Lam和Li在文献[19]中给出的分解公式计算得出。为了便于与实测数据比较,计算时间步长取为30 min。室内外温湿度和水平太阳总辐射得热均为实测数据,如图3-图5所示。

表1 墙体各层材料的物性参数

图3 室内外各时刻温度

图4 室内外各时刻相对湿度

图5 水平太阳总辐射得热

图6为水泥砂浆与砖层分界面处的空气相对湿度的实测值与模拟值比较。从此图可以看出,模拟值跟实测值吻合非常好,模型预测的最大偏差为11.86%,平均偏差为4.44%。砖层与水泥抹灰层的分界面处的空气含湿率模拟值与实测值比较如图7所示,该处模型预测的最大误差为12.91%,平均误差为6.3%。误差的主要原因可能是由于实验测试精度造成的。此外,物性参数不够精确以及求解计算精度问题也是引起误差的一个原因。由于文中提出的计算饱和空气含湿量的计算式计算出的值偏小,因而计算出的相对湿度值偏大。

图6 室外侧分界面处的相对湿度变化

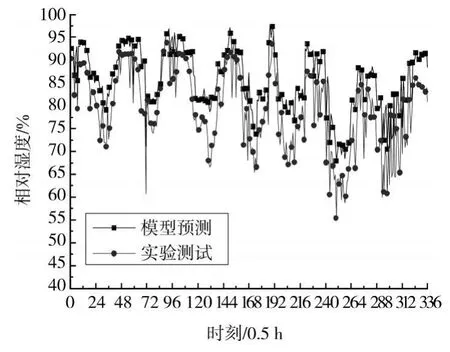
图7 室内侧分界面处的相对湿度变化

图8为室内侧分界面处的温度模拟值跟实测值的比较所示,该处的最大偏差为2.17 K,平均偏差为1.26 K。图9表示室外侧分界面处的温度模拟值跟实测值的比较,在该处模型预测的最大偏差为2 K,平均偏差为1.31 K。偏差的主要原因可能是由于忽略材料的蓄热所引起的。此外,在计算墙体的辐射得热时,只考虑了太阳直接辐射得热而忽略了散射辐射得热,这也是导致偏差的原因之一。

图8 室内侧分界面处温度变化

图9 室外侧分界面处温度变化

4 结论

在Budaiwi模型的基础上,以多孔介质传热传质学中的Fourier定律和Fick定律为基础,以墙体中的空气含湿率和温度为驱动势,根据质量守恒和能量守恒定律对该模型进行了修正;将模型预测结果与实验测试数据进行对比,空气相对湿度最大偏差在15%以内,室外侧分界面处的空气相对湿度平均误差为4.44%,平均温度偏差为1.31 K,室内侧分界面处的空气相对湿度平均偏差为6.3%,平均温度偏差为1.26 K。

[1]QIN M H.Study ofthe hygrothermaltransfer phenomenon in building envelopes[D].La Rochelle:University of La Rochelle,2007.

[2]PHILIP J R,DEVRIES D A.Moisture movement in porous materials undertemperature gradients[J].Transactions of the American Geophysical Union,1957,38(2):222-232.

[3]PEDERSEN C R.Prediction of moisture transfer in building constructions[J].Building and Environment,1992,3:387-397.

[4]KUNZEL H M.Simultaneous heat and moisture transportin building components:one-and two imensional calculation using simple parameters[M].Stuttgart:IRB Verlag,1995.

[5]M ENDES N,PHILIPPI P C.A method for predicting heat and moisture transfer through multilayered walls based on temperature and moisture content gradients[J].International Journal of Heat and Mass Transfer,2005,48(1):37-51.

[6]LUIKOV A W.Heat and mass transfer in capillaryporous bodies[M].Oxford:Pergamon,1966.

[7]QIN M H,BELARBI R,AIT-MOKHTAR A,et al.Coupled heatand moisture transferin multilayer building materials[J].Construction and Materials,2009,23(2):967-975.

[8]QIN M H,BELARBI R,AIT-MOKHTAR A,et al.Simultaneous heat and moisture transport in porous building materials:evaluation of nonisothermal moisture transport properties[J].Journal of Materials Science,2008,43(10):3655-3663.

[9]BELARBI R,QIN M H,AIT-MOKHTAR A,et al.Experimental and theoretical investigation of nonisothermal transfer in hygroscopic building materials[J].Building and Environment,2008,43:2154-2162.

[10]CHEN Y M,WANG S W.Transfer function model and frequency domain validation of moisture sorption in air-conditioned buildings [J]. Building and Environment,2001,36(5):579-588.

[11]闫增峰.生土建筑室内热湿环境研究[D].西安:西安建筑科技大学建筑学院,2003.

[12]QIN M H,BELARBI R.Development of an analytical method for simultaneous heat and moisture transfer in building materials utilizing transfer function method[J].Journal of Materials in Civil Engineering,2005,17(5):492-497.

[13]KAROGLOU M,MOROPOULOU A,K ROKIDA M K,et al.A powerful simulator for moisture transfer in buildings[J].Building and Environment,2007,42(2):902-912.

[14]BUDAIWI I,EI-DIAST Y R,ABDOU A.Modelling of moisture and thermal transient behavior of multilayer non-cavity walls[J].Building and Environment,1999,34(5):537-551.

[15]ANDESSON A C.Verification of calculation methods for moisture transport in porous buildingmaterials[M].Swedish Council for Building Research,1985.

[16]ASHRAE.ASHRAE Handbook 2005 Fundamentals[M].Atlanta:American Society of Heating,Refrigerating and Air-Conditioning Engineers Inc.2005.

[17]KUMARAN M K.Final Report,IEA-Annex 24,Task 3:M aterial Properties[R].Canada:IRC/NRC:1996.

[18]李魁山,张旭,韩星,等.建筑材料等温吸放湿曲线性能实验研究.建筑材料学报,2009,12(1):81-84.LI KUI-SHAN,ZHANG XU,HAN XING,et al.Experimental research of isothermal sorption curve of building materials[J].Journal of Building Materials,2009,12(1):81-84.

[19]LAM J C,LI D H W.Correlation between global solar radiation and its direct and diffusion components[J].Building and Environment,1996,31(6):527-535.