钢管混凝土高墩非线性稳定承载能力可靠度分析

徐腾飞,赵人达,向天宇,杨 成

(西南交通大学桥梁工程系,成都 610031）

西部地区,由于其特殊的地形、地理条件决定了桥梁向高墩、大跨方向发展,在这种形势下,超高墩大跨预应力混凝土连续刚构桥具有很强的竞争优势。钢管混凝土结构具有一系列优越的性能,劲性骨架钢管混凝土桥墩具有广阔的应用前景[1]。利用可靠度研究方法,可以考虑构件抗力的随机性,更加真实的反应钢管混凝土构件的承载能力。传统钢管混凝土可靠度分析方法多依赖于现有钢管混凝土极限承载能力公式,显式的写出极限状态方程,利用一次可靠度法(FORM法或JC法)或者蒙特卡洛方法分析钢管混凝土柱的可靠度[2-4]。而大跨混凝土连续刚构桥中多采用柔性桥墩,尤其是具有明显几何非线性特征的高墩,需考虑结构的几何非线性与混凝土材料非线性的影响,难以得到钢管混凝土结构极限承载能力的显式表达,这限制了可靠度分析的工程应用。为了较准确的模拟钢管混凝土超高墩的结构行为,可利用非线性有限元对整体结构进行非线性承载能力分析。非线性有限元分析可以较准确的反映结构的力学行为,但同时也需消耗大量的机时。直接采用蒙特卡洛方法或者一次可靠度法,计算非线性承载能力可靠度指标,需在进行大量的非线性有限元计算,计算规模过大。

响应面法在验算点附近,用一个显式函数拟合一个曲面来模拟真实的失效曲面,建立结构输入与结构响应的关系,然后进行可靠性分析[5]。其优点是通过有限次数的非线性有限元计算得到显式的承载能力近似表达式,大大简化可靠度指标计算工作量,有利于可靠度分析方法在工程推广。

该文采用响应面方法与钢管混凝土非线性有限元程序拟合钢管混凝土结构的非线性承载能力的显式方程,然后利用一次可靠度法求得钢管混凝土结构可靠度指标。同时考虑到超高墩的施工误差,本文利用一致缺陷模态法考虑桥墩的初始几何缺陷对可靠度指标的影响。结合四川雅泸高速公路中,全线最高达182.78 m的桥墩(腊八斤特大桥),展开参数分析,探讨长细比,偏心距,径厚比,几何非线性与初始几何缺陷对可靠度指标的影响。

1 基本原理

常用的响应面法为以求得验算点为目的的迭代的二次多项式序列响应面法,即对n个随机变量X1,X2,…,Xn的情况,将近似函数取为不含交叉项的二次多项式形式:

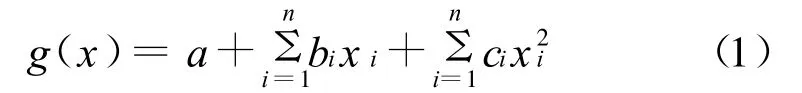
其中:a、bi、ci(i=1,2,…,n)为响应面的待定系数,可以由中心复合设计(2n+1次试验)回归得到[6]。

钢管混凝土结构承载能力非线性可靠度分析主要流程为:

预计算,按照加载工况,对钢管混凝土桥墩进行非线性有限元分析,获取一阶屈曲模态。

第1步,以第k步验算点Xk={xi,i=1…n}为中心,样本点选择为(xi-λ σx)与(xi+λ σx),建议 λ的取值为1～5。根据经验,当可靠度指标较大时,选择较大的λ有利于迭代收敛。

第2步,对2n+1个采样点中的标准正态空间随机变量转换为基本变量。

第3步,进行对2n+1个基本机变量代入非线性有限元模型,进行非线性有限元计算,以确定待定系数,生成与标准正态随机变量相关的响应面。

第4步,利用一次可靠度法,计算响应面函数的验算点Xk+1。

第5步,计算收敛条件|Xk-Xk+1|＜ε,如果满足,计算可靠度指标β,否则转回第一步,继续迭代。

2 非线性有限元统计模型

表1给出了钢管混凝土工程实践中,常用材料的性能指标统计,钢材与混凝土强度均服从正态分布[7]。在非线性分析中,钢材应力应变关系采用理想弹塑性模型;混凝土受压区采用韩林海[1]建议的应力应变关系,混凝土受拉区采用弹脆性模型。

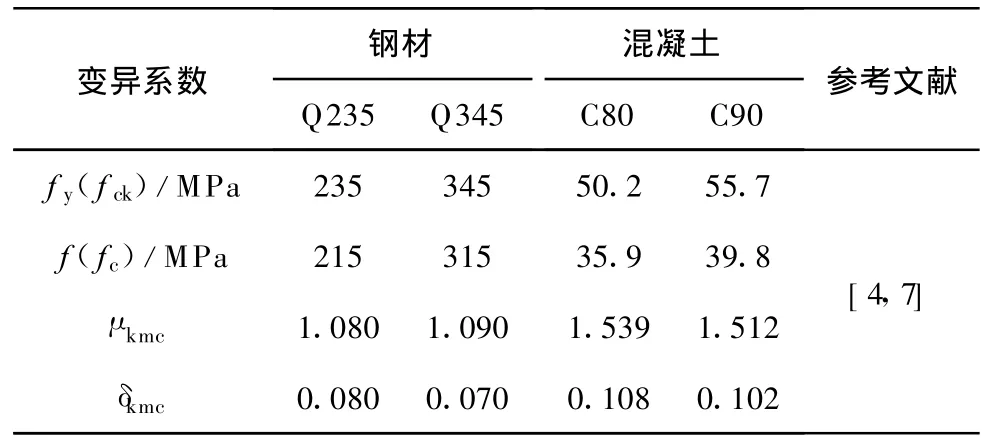
表1 材料性能指标统计表

利用一致缺陷模态法[8]考虑钢管拱过程中的初始几何缺。钢管混凝土结构的一阶屈曲模态需根据非线性有限元分析确定。最大初始几何缺陷,根据文献[9]中规定取为l/1000,变异系数假设为5%,l取钢管长度。

本文利用退化梁单元理论[10]编制非线性有限元程序,采用修正的拉格朗日描述来考虑结构几何非线性,并利用弧长法[11-13]求解非线性有限元问题,得到钢管混凝土结构全过程受力行为。退化梁单元的实质是:用中面节点位移表示三维结构的位移场,而几何方程与物理方程均基本沿用三维结构的方程。为了用中面节点位移表示三维结构的为异常,一般均采用铁木辛克梁理论假设:垂直于中面的直法线变形后仍然为直的,但是不假设其垂直于梁轴线。在单元刚度矩阵形成中,采用截面上采用分层或分块积分的方法。为防止“剪锁”现象,采用缩减积分技术,选择每个分块的中点作为高斯积分点。

根据文献[1]的建议,极限承载能力的确定依据为:钢材进入屈服,混凝土达到峰值应力[1]。在数值程序编制中,利用弧长法求解可以得到考虑材料非线性与几何非线性的结构受力全过程的力—位移曲线,对于有软化段的结构可以根据力—位移曲线进入下降段(即弧长法计算得到的荷载系数(λ)小于0)来判断达到极限承载能力;对于表现为接近理想弹塑性的结构则当力—位移曲线达到屈服时,认为达到极限承载能力。

3 可靠度指标计算与敏感性系数

定义功能函数G:

其中U为结构非线性极限承载能力,S为荷载效应。

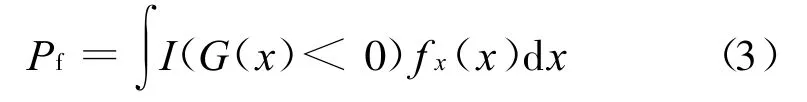
式中Pf为结构失效概率;I为指标函数,当G(x)＜0时,取值为1,否则取值为0;fx(x)为变量x的概率密度函数。

可靠度指标定义为

灵敏度分析就是用来确定随机变量及其分布参数对于计算失效概率的重要性,求解灵敏度的方法通常采用差分法[14-15]。该文采用中心差分法定义敏感性系数:

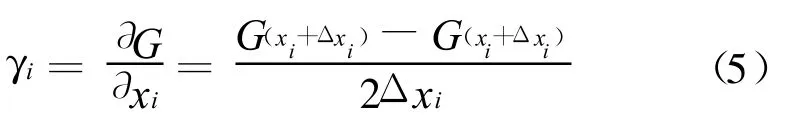
为了更易于敏感系数的比较,通常对{γi}进行归一化处理。

4 高墩算例与参数分析

腊八斤特大桥中 10号墩为最高墩,墩高182.78 m,如图1所示,主墩采用钢管混凝土叠合柱,墩顶横桥向7 m,横桥向为等宽,顺桥向墩顶宽10.0 m,按70:1的比例向下变宽放坡;腹板厚为50 cm的钢筋混凝土。钢管尺寸为φ 132.018 mm,钢管内灌注C80混凝土,该文算例中S的取值为:桥墩最不利设计荷载为轴力140595 kN,偏心距0.57 m,偏心方向为顺桥向。

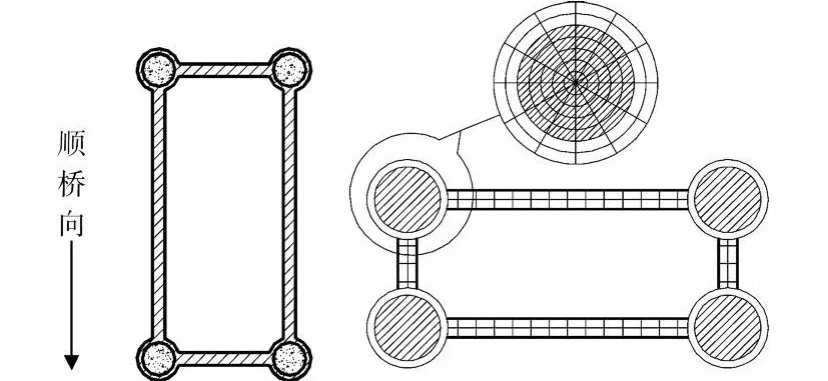
图1 钢管混凝土桥墩截面形式与截面分块示意

算例1 按照设计中放坡方式,选取钢管混凝土桥墩的高度参数:12～320 m,即长细比为3.2至62.1,计算设计荷载作用下,功能函数G的可靠度指标,并给出不考虑几何非线性与不考虑初始几何缺陷的可靠度指标对比,如图2所示。由计算结果可以看出,随着长细比的增大,钢管混凝土超高墩刚度减小,因此几何非线性与初始缺陷的影响逐渐增大,可靠度指标逐渐降低。在柔性钢管混凝土桥墩中应该考虑初始几何缺陷的影响。

算例2 选取高度为182.78 m的钢管混凝土超高墩,变化设计荷载的偏心距0～4m,计算功能函数G的可靠度指标,并在图3中给出不考虑初始几何缺陷的可靠度指标对比。由图中可以看出随着初始偏心距的增大,可靠度指标降低;同时由于初始偏心距的增大,使初始几何缺陷在初始偏心距中占的比例逐渐减小,掩盖了初始几何缺陷的对承载能力降低的贡献。图4给出了混凝土强度对可靠度指标的敏感系数。由图中可以看出混凝土强度的敏感性系数逐渐降低。这是由于初始偏心距的增大,使桥墩受力由轴压状态逐渐转变为小偏心受压,乃至达到大偏心受压状态,其破坏形式也由混凝土受压破坏逐渐转换为钢材受拉破坏。可以预测,当桥墩处于大偏心状态,此时的钢管混凝土中的混凝土大量处于受拉开裂状态,结构破坏时,混凝土大量开裂,受压混凝土未达到抗压极限强度。因此通过提高混凝土标号或利用套箍效应提高混凝土极限抗压强度,对大偏心的钢管混凝土高墩承载能力影响有限。

图2 可靠度指标与长细比

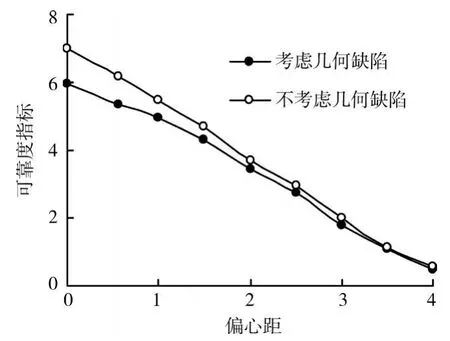
图3 可靠度指标与偏心距

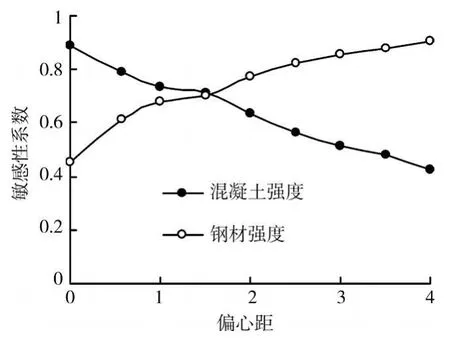
图4 混凝土强度敏感性系数与偏心距

算例3 选取实际采用的182.78 m的钢管混凝土超高墩,变化钢管壁厚t,径厚比为16～132,计算设计荷载作用下,功能函数G的可靠度指标,并给出不考虑几何非线性与不考虑初始几何缺陷的可靠度指标对比,如图5所示。随着径厚比的增大,可靠度指标逐渐增大。钢管混凝土桥墩承载能力的提高主要来源两个方面:首先径厚比的增大加强套箍效应导致混凝土极限抗压强度的提高,其次径厚比的增大提高了钢管混凝土桥墩的含钢率。由算例2的敏感性分析可以看出,当轴压或者小偏心受压时,钢管混凝土桥墩全截面以受压为主,此时由于套箍效应提高的混凝土极限抗压强度对可靠度指标提高贡献较大;随着偏心距的增大,在大偏心受压情况下,钢材强度的敏感性系数逐渐提高,含钢率对可靠度指标的贡献较大。

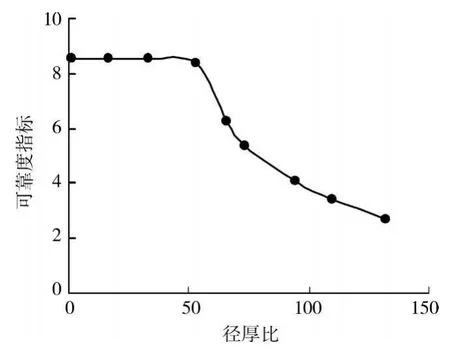
图5 可靠度指标与径厚比

5 结论

大跨刚构桥梁中采用的钢管混凝土叠合柱式高墩具有刚度小,长细比大的特点,在其稳定承载能力研究与稳定可靠度研究中,需考虑几何非线性与初始几何缺陷,否则将会高估桥墩的可靠度指标。桥墩的初始几何缺陷在初始偏心距较小的时候对桥墩承载能力影响较大,当初始偏心距较大时,会掩盖初始几何缺陷的影响。钢管混凝土叠合柱式高墩以偏心受压为主要受力形式,当轴心受压时小偏心受压时,混凝土强度的可靠度指标敏感性系数较高;当大偏心受压时混凝土强度的影响就相对有限。

针对参数分析结果,此类钢管混凝土叠合柱式桥墩可通过:限制桥墩长细比;小偏心受压控制的桥墩,可提高混凝土标号或提高径厚比以加强套箍效应;大偏心受压控制的桥墩,可提高钢材强度与提高径厚比以增加含钢率等措施提高承载能力可靠性。

[1]韩林海.钢管混凝土结构——理论与实践[M].北京:科学出版社,2004.

[2]周圣斌.钢管混凝土柱极限承载力可靠度校准分析[J].建筑科学,2009,25(3):79-81.ZHOU SHENG-BIN.Reliability analysis of ultimate bearing capacity of concrete-filled steel tube column[J].Building Science,2009,25(3):79-81.

[3]陶忠,韩林海,杨华.钢管混凝土构件设计计算及可靠度分析[J].工业建筑,2000,30(6):1-6.TAO ZHONG,HAN LIN-HAI,YANG HUA.Design calculation of concrete filled steel tubular members and reliability analysis[J].Industrial Construction,2000,30(6):1-6.

[4]余志武,贺飒飒.钢管混凝土短柱极限承载力可靠度分析[J].工程力学,2006,23(11):139～144.YU ZHI-WU,HE SA-SA.Reliabilityanalysis of ultimate bearing capacity of concrete-filled tubular steel stub columns[J].Engineering Mechanics,2006,23(11):139:144.

[5]XUAN SON NGUYEN, ALAIN SELLIER,FREDERIC DUPRAT,etal.Adaptive response surface method based on a double weighted regression technique[J].Probabilistic Engineering Mechanics,2009,24(2):135-143.

[6]HENRI P GAVIN,SIU CHUNG YAU.High-order limit state functions in the response surface method for structural reliability analysis[J].Structural Safety,2008,30(2):162-179.

[7]赵国藩,金伟良,贡金鑫.结构可靠度理论[M].北京:中国建筑工业出版社,1990.

[8]唐敢,赵惠麟,赵才其.板片空间结构缺陷稳定分析及试验研究[J].土木工程学报,2008,41(8):15-21.TANG GAN,ZHAO HUI-LING,ZHAO CAI-QI.Theoretical and experimental study on the stability of sheet space structures with imperfections[J].China Civil Engineering Journal,2008,41(8):15-21.

[9]蔡绍怀.现代钢管混凝土结构[M].修订版.北京:人民交通出版社,2007.

[10]XIANG TIANYU,TONG YUQIANG,ZHAO RENDA.A general and versatile nonlinear analysis program for concrete bridge structure[J].Advances in Engineering Software,2005,36(10):681-690.

[11]MANUEL RITTO-CORREA,DINAR CAMOTOM.On the arc-length and other quadratic control methods:Established, lessknown and new implementation procedures[J].Computers&Structures,2008,86(11-12):1353-1368.

[12]MULU,ARTURO E SCHULTZ,HENRYKK.STOLARSKI.Application of the arc-length method for the stability analysis of solid unreinforced masonry walls under lateral loads[J].Engineering Structures,2005,27(6):909-919.

[13]CK KUNDU,PK SINHA.Post buckling analysis of laminated composite shells[J].Composite Structures,2007,78(3):316-324.

[14]JUNHO SONG,WON-HEE KANG.System reliability and sensitivity under statistical dependence by matrixbased system reliability method[J].Structural Safety,2009,31(2):148-156.

[15]S KUCHERENKO,M RODRIGUEZ-FERNANDEZ,C PANTELIDES,etal.Monte Carlo evaluation of derivative-based global sensitivity measures[J].Reliability Engineering&System Safety,2009,94(7):1135-1148.