黑龙江省东部小黑杨一元立木材积表的编制

2010-11-09杨胜涛尹小康孙元发

黑龙江生态工程职业学院学报 2010年2期

关键词：样木立木材积

杨胜涛尹小康孙元发

(黑龙江省林业勘察设计院,哈尔滨 150080)

黑龙江省东部小黑杨一元立木材积表的编制

杨胜涛尹小康孙元发

(黑龙江省林业勘察设计院,哈尔滨 150080)

根据黑龙江省东部小黑杨人工林的分布情况,采集了 4 566株编表样木数据,编制了黑龙江省东部小黑杨一元立木材积表。经检验,本材积表在该地区精度高、适用性强,可供生产经营单位、管理部门和科学研究使用。

小黑杨;一元;材积表

黑龙江省东部自 70年代末到 80年代初,营造了大面积的小黑杨人工林,到目前为止面积约为 25万 hm2,活立木蓄积2 000万 m3。其中,进入抚育间伐和主伐的森林面积占总面积的 80%,包括农田防护林、水土保持林、用材林。在其经营管理过程中,一直使用小叶杨或中东杨的一元立木材积表,在生产上产生单株材积小于出材量的严重问题。随着林权制度改革的深化和森林资源管理的进一步规范,编制适于黑龙江省东部的小黑杨立木材积表迫在眉睫。

1 基础数据的来源

根据黑龙江省东部小黑杨人工林的实际分布情况,选择东部典型县(市、区),分别不同年龄和立地条件设置小黑杨人工林样地,进行编表样木的调查,共收集了4 566株编表样木数据。样木数据情况见表1。

表1 编表样木的来源与数量

本次调查,以 5cm为起测径阶。样木伐倒后,以 1m为一区分段长,按中央断面积区分求积法用围尺量测各区分段及胸高部位的带皮直经 (精确到0.1cm),用皮尺测量树高 (精确到0.1m)。将外业所调查的胸径、树高及各区分段的中央直径,建立数据库,并按中央断面积区分求积计算各样木的材积。

2 数据整理

将各样木的胸径 (D)、树高 (H)及材积 (V)建立数据库作为本次编制和检验材积表的基础数据。

2.1 异常数据的剔除

异常数据的剔除过程分两步进行。首先,分别绘制 VD散点图,通过肉眼观察确定出明显远离样点群的数据并删除;其次是用全部数据拟合对数线性化以后的一元材积式,并绘制模型预估值与标准化残差之间的残差图。在残差图中,超出 ±2倍标准差以外的数据作为极端观测值予以剔除。

2.2 数据整理

剔除异常数据后,将所收集的全部样木分成两组独立样本:编表样本和检验样本。编表样本共有4 085株样木。在全部样木中随机选取 455株样木组成独立检验样本。

有关小黑杨人工林编表样本和检验样本按径阶样木数的分布及其统计量详见表2、表3。从表中可以看出,各径阶株数的分布近似正态分布,符合编表要求。

表2 小黑杨人工林编表样本按径阶统计量

表3 小黑杨人工林检验样本按径阶统计量

3 立木材积表的编制与检验

3.1 立木材积表的编制方法

本次编表在拟合小黑杨人工林的一元材积式时,并未采用传统的按径阶归类后株数加权的方法,而是将各样木作为一个样点进行散点拟合。一元材积式的基本模型为:

式中:V——立木材积 (m3);D——胸高直径 (cm);a和b——模型待定系数。

采用阻尼最小二乘法Marquardt迭代法,将对数线性化后所得到的参数作为迭代的初始参数,直接拟合 (1)式,使达到最小,并求得参数 a和 b的全局最优解。同时计算一些拟合统计量:

式中:p为参数个数,对一元材积式 p=2。

3.2 立木材积方程的拟合结果及参数检验

对小黑杨人工林编表数据,采用非线性回归模型迭代法估计了一元材积方程 (1)式的参数,并在α=0.05的显著水平下进行了材积方程参数的显著性检验,结果见表4。采用非线性回归模型迭代法拟合的小黑杨人工林一元材积方程(1)式的拟合图详见图1。

表4 非线性回归模型迭代法估计的一元材积方程(1)的参数及参数检验结果 α=0.05

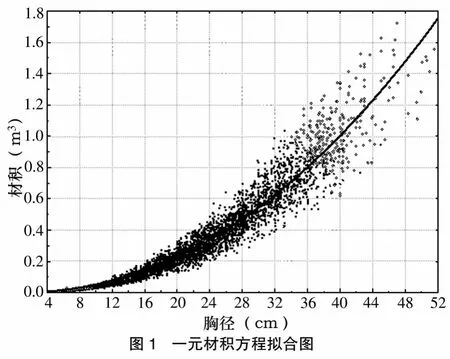
由表4可知,利用非线性模型估计的小黑杨人工林一元材积方程 (1)式的各参数,在0.05显著水平下均差异显著,说明所建模型均有效。由模型拟合效果来看,相关指数高达0.924 5,剩余标准差小于0.006 5m3,总体拟合效果极佳 (见图1)。

3.3 材积方程的适用性检验

3.3.1 材积表的误差分析

设实测的各样木材积为 yi,而材积表材积为 xi。本研究采用独立的检验样本对材积表的检验主要分析以下几种误差:

3.3.2 材积表的预估精度及置信椭圆 F检验

预估精度计算及置信椭圆 F检验方法,是实测材积 (y)与材积表材积 (x)之间建立一元线性回归方程:

由检验数据(xi,yi)(i=1,2,……,n),采用最小二乘法估计一元线性回归模型 (2)的回归系数α和β的估计值 a和b,并计算出回归标准差 (Sy·x),回归标准误 (Sy)、误差限 (Δ)及相对误差限(E%):

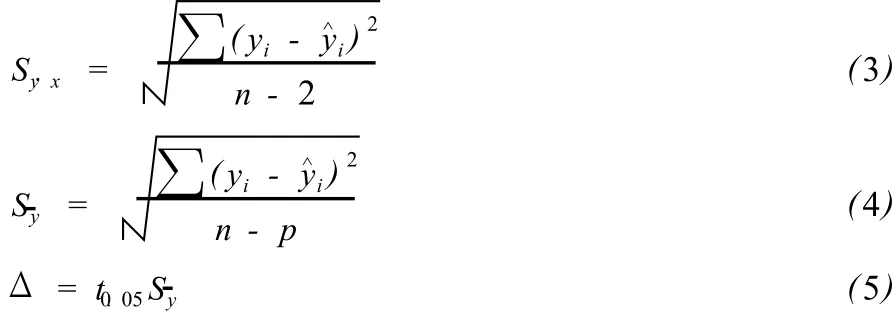
材积表的预估精度(P%):

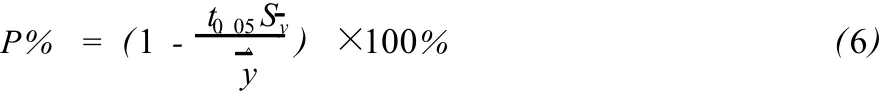
置信椭圆 F检验则是在置信水平取为 1-α时,对回归模型系数α和β构造联合置信区域。这个区域由下式给出:

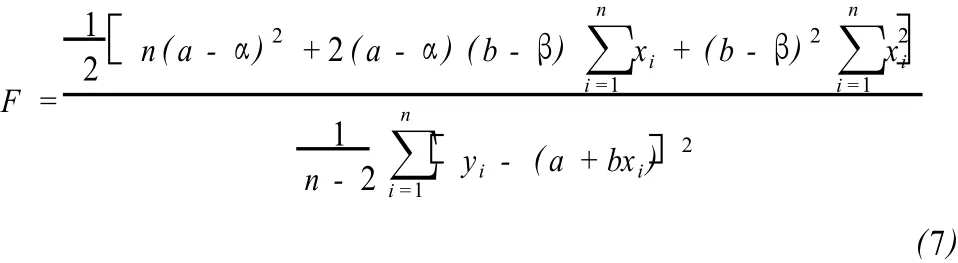
从而一次完成对回归系数α和β的显著性检验。

显然,如果材积表材积 (x)与实测材积 (y)完全一致,则α =0,β=1。但实际上往往不一致。因此,需要检验由样本估计的 a和 b的值与它们的真值之间有无显著差异。将α=0,β=1代入 (7)式可得:

式中:n为检验样木的株数,yi为实测材积,xi为理论材积,a、b为回归直线的参数。

(8)式服从自由度 f1=2,f2=n-2的 F分布。这个置信区域的边界是以 (a,b)为中心的椭圆。根据按 (8)式计算的 F值与α显著水平下的理论 Fα值,来判断材积表的适用性。当检验结果无显著差异时,则材积表适用于调查地区;反之材积表产生较大误差,则不适用,需进行修正或重新编表。

3.3.3 材积表的检验结果

采用独立检验数据(见表3),对新建的小黑杨人工林一元立木材积式进行了材积误差分析、预估精度及置信椭圆 F-检验等材积表的适用性检验,检验结果见表5。

表5一元立木材积式的适用性检验结果n=570,α=0.05

从表5中的一元材积方程的误差分析结果及预估精度来看,无论是平均误差 (M E)、绝对平均误差 (MAE)和系统误差 (SE%)还是预估精度,两者相差无几。从置信椭圆 F-检验结果来看,一元积式在 0.05显著水平下差异不显著,且各材积表的相对误差 (M%E)小于 ±5%,系统误差 (SE%)均小于 ±1%,一元材积表的预估精度均大于 97%。这表明所编制的一元材积表的材积与实测材积之间无显著差异,满足精度要求,可以在生产中推广使用。