可连续光滑偏转后缘的变弯度翼型气动特性分析

陈 钱,白 鹏,尹维龙,冷劲松,詹慧玲,刘子强

(1.中国航天空气动力技术研究院,北京100074；2.哈尔滨工业大学航天学院,黑龙江哈尔滨,150080)

0 引 言

先进飞行器对更优性能的追求始终是空气动力学研究的重要推动力,其与近年来智能材料和结构新进展一起,使人们开始重新关注飞行生物空气动力学在飞行器上的应用,如 Lentink等[1]在2007年曾于《Nature》上指出雨燕飞翔时的“变形”在未来飞机发展中具有重要作用。

上述构想的可“变形”的飞行器主要特点在于:能根据环境变化和任务变化来灵活地改变其形状和尺寸,以得到满足环境和任务要求的气动、结构和控制特性以及总体性能。

已有研究中,飞行器的变形方式可分为三类:大尺度变形、中等变形以及局部小变形。对于大尺度变形,变形概念创新及其实现十分关键。在最近的大型研究项目“Morphing Aircraft Structure”项目中,主要确立了蝙蝠翼方案[2]和折叠翼方案[3]。对于中等变形,具有代表性的工作有:“Mission Adaptive Wing”项目[4]的研究者采用光滑地改变前缘和后缘弯度的机翼,获得了巡航性能、机动性能等方面的改进；“Active Flexible Wing/Active Aeroelastic Wing”项目[5]的研究者采用副翼和前缘襟翼的偏转来改变柔性机翼上的气动力,进而控制柔性机翼的扭转变形,在不增加飞机重量的情况下显著提高了滚转控制性能；“Smart Wing”项目[6]的研究者采用无铰接的、连续光滑的、大偏转角的、高驱动速率的操纵面,最终获得了更优的滚转和俯仰控制性能。对于局部小变形,同样具有许多活跃的研究主题,如“Morphing”项目[7]中将结构自适应变形技术与主动流动控制技术相结合所开展的一系列微流动自适应控制研究。无论是采用合成射流技术[8]、脉冲射流技术[9]等的“虚拟形状变化”[10],还是采用小尺度局部结构主动实际变形(如跨声速翼型激波附近的局部轮廓线变形[11]),都能对飞行器局部流场结构产生有利影响,进而提高飞行器的性能。

本文致力于研究上述中等变形中的变弯度翼型,即采用了无铰接的、连续光滑的后缘操纵面的翼型。因为从已有文献来看,已研究了采用这种变形方式的变弯度翼型与传统主翼-简单襟翼翼型的气动特性,并开发了使后缘操纵面的偏转角度范围和偏转速率达到实际需求的技术；然而,关于变形参数对气动特性的影响及气动特性的产生机理,还有待研究。本文对这一内容开展探索,即分析不同的可连续光滑偏转后缘的翼型与传统主翼-简单襟翼翼型的气动特性,讨论光滑变形方式中的可变形段范围、转轴位置、后缘偏转角度、后缘高度这四个因素对气动特性的影响,并从翼型表面压力分布和翼型表面附近流场结构的角度研究气动特性的产生机理；同时,研制可连续光滑偏转后缘的变弯度翼型实验模型,并进行风洞测力实验,验证与确认可连续光滑偏转后缘的变弯度翼型的可实现性。

1 可连续光滑偏转后缘的变弯度翼型

图1给出了以NACA 2412翼型为基础的变弯度翼型。图中,“BA”指基本翼型(basic airfoil),即NACA 2412翼型；“CD”指传统偏转(conventional deflection),即传统主翼-简单襟翼翼型[12](转轴位于70%弦长处,偏转 15°)；“SM-1”指第一种光滑变形(smooth morphing),即可变形段范围从基本翼型50%弦长处到70%弦长处的变弯度翼型,其后缘与传统主翼-简单襟翼翼型后缘偏转相同高度不同角度(转轴位于60%弦长处,偏转11°能获得与传统主翼-简单襟翼翼型后缘相同的高度)；“SM-2”指第二种光滑变形,即可变形段范围从基本翼型50%弦长处到70%弦长处的变弯度翼型,但其后缘与传统主翼-简单襟翼翼型后缘偏转相同角度不同高度(转轴位于60%弦长处,偏转15°)；“SM-3”指第三种光滑变形,即可变形段范围从基本翼型50%弦长处到90%弦长处的变弯度翼型(转轴位于70%弦长处,偏转15°),其后缘与传统主翼-简单襟翼翼型后缘偏转相同高度相同角度；“SM-4”指第四种光滑变形,即可变形段范围从基本翼型60%弦长处到80%弦长处的变弯度翼型(转轴位于 70%弦长处,偏转 15°),其后缘也与传统主翼-简单襟翼翼型后缘偏转相同高度相同角度。

2 计算与实验方法

本文数值计算中采用的基本方程为不可压缩流动Reynolds平均Navier-Stokes方程:

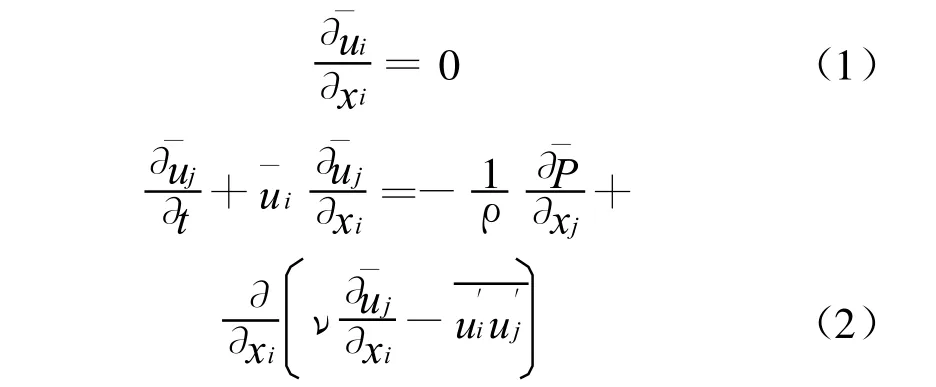
其中,带上标“-”的量为 Reynolds平均量,其它符号意义限于篇幅不再列出。

根据以往湍流数值模拟研究的经验,采用剪切应力输运(SST)模型作为湍流模型。

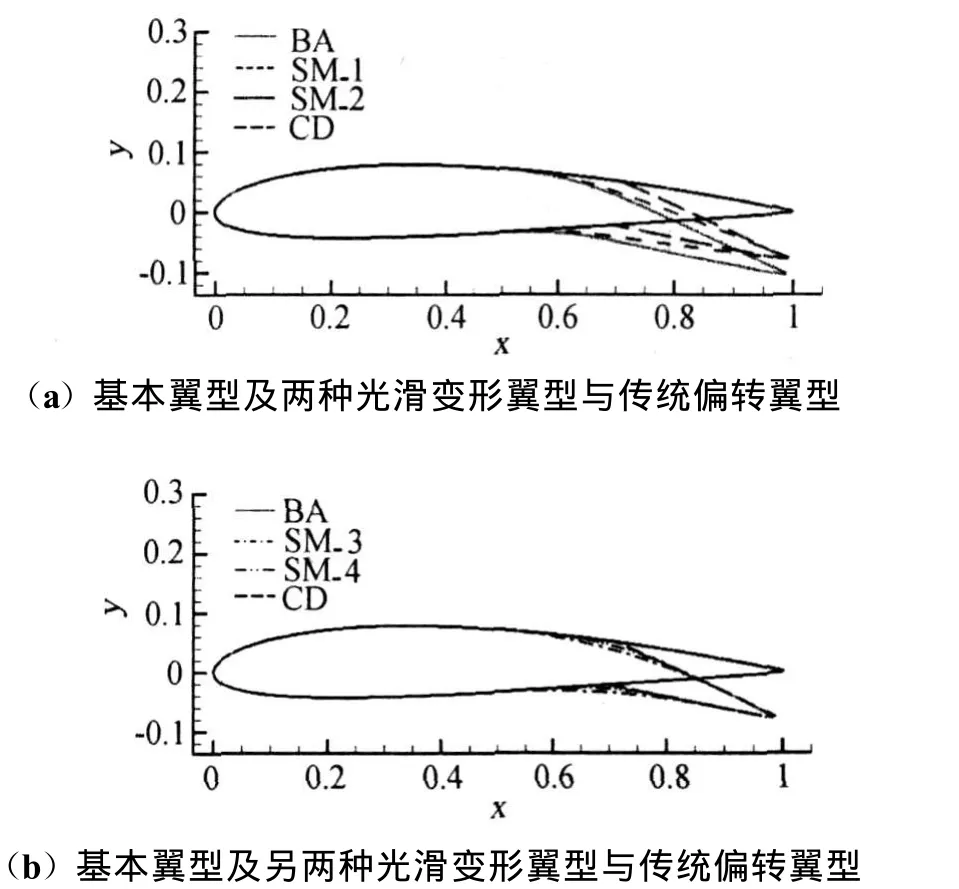
图1 以NACA 2412为基础的六种翼型Fig.1 Six airfoils based on NACA 2412

计算中,自由来流速度V为60m/s,Reynolds数Re约为4.1×106。外边界(即远场)采用自由流边界条件,内边界(即翼型壁面)采用无滑移固壁边界条件。

本文采用SIMPLE算法求解上述问题。当迭代到基本变量和湍流变量的残差均比最初迭代时的残差小3个数量级且流场全局量与上一次迭代结果相差小于0.01%时,认为收敛到定常状态数值解。

本文还研究了网格密度对计算结果的影响,最终采用了537×131(弦向×法向)的网格。

第1节中给出的可连续光滑偏转后缘的变弯度翼型,在本文得到了结构上的实现并进行了风洞实验测试,这里给出实验方法(模型结构和测试结果见第4节)。实验在中国航天空气动力技术研究院FD-10风洞进行。风洞实验段尺寸为0.6m×0.6m(本文进行翼型实验时增加了侧挡板,以使实验模型绕流尽可能为二维流动),自由来流速度V为12m/s(第4节中与实验进行比较的计算,其自由来流速度V为12m/s,Reynolds数Re约为8.2×105)。实验中采用六分量天平测量实验模型所受的轴向力、法向力、俯仰力矩(天平的这三个分量量程分别为 9.8N,29.4N,0.882 N◦m),采用风速管和风速传感器测量来流的速度。实验模型相对于来流的攻角采用专门设计的变攻角机构来控制(模型采用侧支撑)。对于某一确定的实验模型外形,数据采集程序采集1000个数据点并取平均值,随后重复实验多次,取重复性较好的多次结果平均,作为该外形的原始数据；在此基础上,数据采集程序先将天平轴系的数据根据天平轴系与实验模型体轴系的关系换算为体轴系的数据,再将体轴系的数据根据实验模型相对于来流的攻角换算为风轴系的数据。

3 计算结果分析

在详细分析计算结果之前,有必要对计算方法进行验证与确认。图2给出了采用上述计算方法得到的NACA 2412翼型升力系数和阻力系数与文献[12]中的实验结果的比较,图中呈现的一致性表明了计算方法的准确性。

图2 本文计算结果与文献[12]中实验结果的比较Fig.2 Comparison of computation results in this paper and experiment results in Ref.[12]

3.1 连续光滑变形翼型与传统偏转翼型的气动特性比较

图3给出了变弯度NACA 2412翼型六种外形在各种攻角下的升阻比。由图可见,光滑变形与传统偏转均使得翼型的升阻比曲线左移,而光滑变形翼型的升阻比明显优于传统偏转翼型的升阻比,即“SM-1(符号说明见第1节,下同)”的升阻比在大的负攻角附近和大的正攻角附近均略小于传统偏转翼型的升阻比,而在中间宽广的攻角范围内大于传统偏转翼型的升阻比(升阻比的改进在6°攻角时最大,达92%)；“SM-2”的升阻比在大的正攻角附近略小于传统偏转翼型的升阻比,而在宽广的其它攻角范围内大于传统偏转翼型的升阻比(升阻比的改进在-10°攻角时最大,达148%)；“SM-3”的升阻比在大的负攻角附近与传统偏转翼型的升阻比十分接近,在中间宽广的攻角范围内大于传统偏转翼型的升阻比(升阻比的改进在6°攻角时最大,达88%),在大的正攻角附近略小于传统偏转翼型的升阻比；“SM-4”的升阻比在大的负攻角附近和大的正攻角附近均与传统偏转翼型的升阻比十分接近,在中间宽广的攻角范围内大于传统偏转翼型的升阻比(升阻比的改进在6°攻角时最大,达59%)。上图所反映出的光滑变形翼型的升阻比明显优于传统偏转翼型的升阻比,可以从图4(以BA,SM-3,SM-4,CD为例)的变弯度NACA 2412翼型四种外形在各种攻角下的升力系数和阻力系数来进一步分析。从图4(a)可见,光滑变形翼型的升力系数在4°至10°的攻角范围内明显大于传统偏转翼型的升力系数,但从图4(b)可见,光滑变形翼型的阻力系数在2°至12°的攻角范围内明显小于传统偏转翼型的阻力系数；因而,光滑变形翼型相对于传统偏转翼型,其升阻比的改进会很显著。

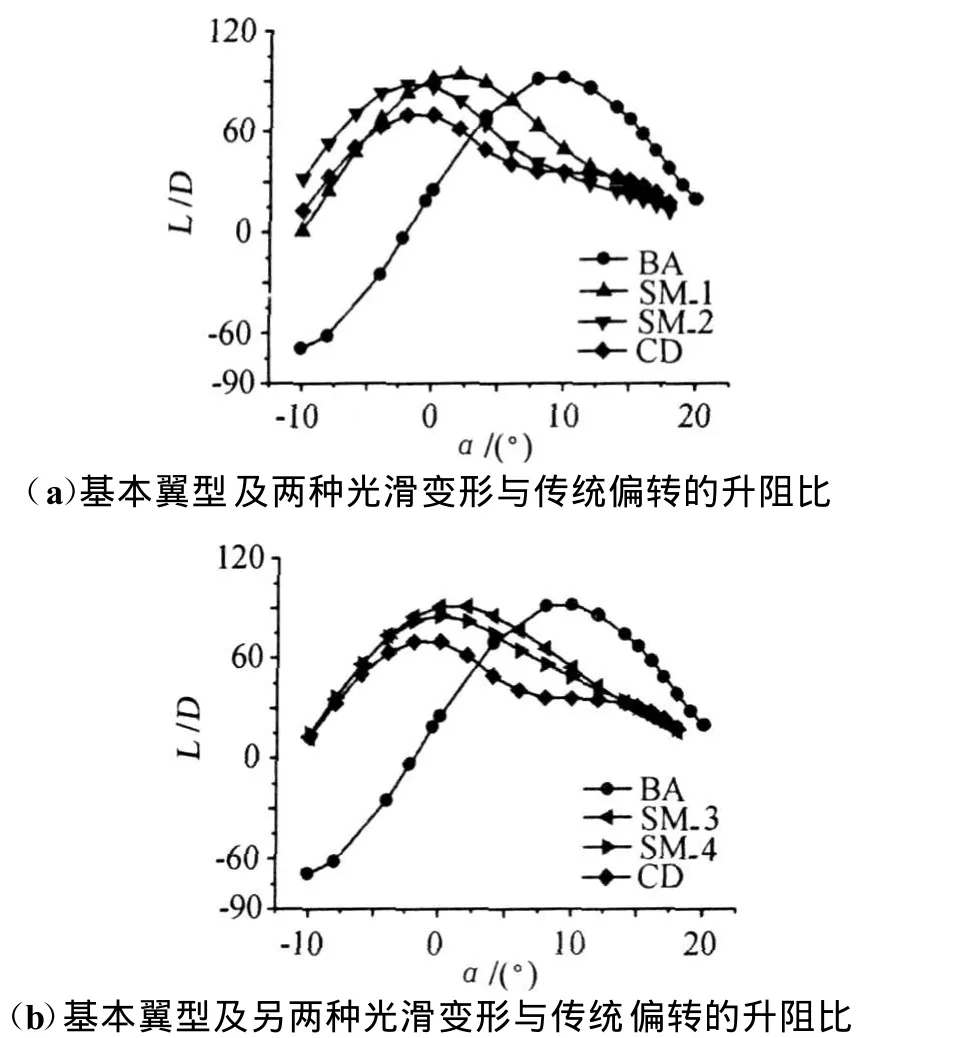
图3 变弯度NACA 2412翼型六种外形的升阻比Fig.3 Lift-to-drag ratio of variable camber NACA 2412 airfoil in its six shapes

图4(c)给出了四种外形的俯仰力矩系数。由图可见,光滑变形翼型的低头俯仰力矩系数在4°至10°的攻角范围内明显大于传统偏转翼型的低头俯仰力矩系数。这表明,光滑变形翼型相对于传统偏转翼型,其俯仰控制性能具有显著改进。

图4 变弯度NACA 2412翼型四种外形的升力系数和阻力系数以及俯仰力矩系数Fig.4 Lift coefficient,drag coefficient and coefficient of pitch moment of variable camber NACA 2412 airfoil in its four shapes

3.2 变形参数对连续光滑变形翼型气动特性的影响

本文第1节给出了四种不同的连续光滑变形翼型,归纳起来,它们的不同点有四个方面:(1)可变形段范围；(2)转轴位置；(3)后缘偏转角度；(4)后缘高度。

实际上,比较光滑变形翼型与传统偏转翼型的气动特性,其前提是光滑变形翼型与传统偏转翼型在外形上具有可比性。然而,准确地定义可比性,本身就是需要研究的内容。本文研究多种光滑变形方式,即为对可比性的探索；最终,本文确定了一类具有较好可比性的光滑变形方式:使光滑变形翼型的可变形段中点位于转轴位置、转轴位置与传统偏转翼型转轴位置相同、可变形段之后的刚性段与传统偏转翼型转轴之后的刚性段偏转相同的角度并达到相同的高度。第三种和第四种光滑变形方式符合这类光滑变形方式的特点,本文对其进行了重点分析；另外,也分析了第一种和第二种光滑变形方式。

对于第一种和第二种光滑变形方式,它们的可变形段范围和转轴位置均相同,但第一种光滑变形方式为了使后缘与传统偏转翼型后缘达到相同高度,其与传统偏转翼型的后缘偏转角度不同,而第二种光滑变形方式为了使后缘与传统偏转翼型后缘达到相同角度,其与传统偏转翼型的后缘高度不同。这两种光滑变形方式的升阻比(见图3(a))相差较大,后者近似于将前者往左平移,但后者比前者的最大升阻比小。第一种和第二种光滑变形方式的气动特性产生这种差异,原因可能在于:后者的偏转角度和偏转高度均更大。

对于第三种和第四种光滑变形方式,它们的可变形段范围不同,但转轴位置、后缘偏转角度、后缘高度均相同。从图3(b)可见,第三种比第四种光滑变形方式的气动特性更优。这可进一步从图4(a)的升力系数、图4(b)的阻力系数看出。第三种和第四种光滑变形方式的气动特性产生这种差异,原因可能在于:可变弯度翼型的后缘偏转需要一定的过渡段,合适的过渡段能提高气动性能；具体地说,第三种光滑变形方式的可变形段从基本翼型50%弦长处到90%弦长处,第四种光滑变形方式的可变形段从基本翼型60%弦长处到80%弦长处,而传统偏转可认为其可变形段长度为零(即集中于基本翼型70%弦长处这一点),从计算结果中的气动特性来看,可能可变形段范围越大,气动特性越优。然而,若综合考虑气动特性和结构实现上的经济性,则会存在一个使得综合性能最优的可变形段范围。

3.3 气动特性的产生机理

对于以上分析和讨论的气动特性,可从翼型表面压力分布和翼型表面附近流场结构的角度,来进一步研究其产生机理。

图5给出了变弯度NACA 2412翼型三种外形在四种攻角下的表面压力系数。

特别需要注意的两个方面是:(1)传统偏转翼型上下表面压力系数曲线所围成的面积与光滑变形翼型上下表面压力系数曲线所围成的面积不相同,特别是6°攻角时(图5(c))这种面积之差更为明显(该攻角下,这种面积对于 SM-3最大,对于SM-4次之,对于传统偏转最小)；(2)图5中传统偏转翼型表面压力系数曲线在转轴位置(70%弦长处)出现了突跃,而光滑变形翼型表面压力系数曲线在转轴位置(同样也是70%弦长处)却十分平滑。这两个方面的差别是光滑变形翼型与传统偏转翼型具有不同气动特性的主要原因。

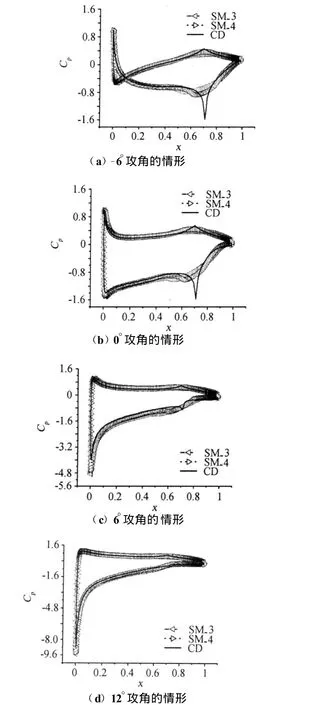
图5 弯度NACA 2412翼型三种外形的表面压力系数Fig.5 Surface pressure coefficient of variable camber NACA 2412 airfoil in its three shapes

比较图5中四幅子图可见,上述压力“突跃”随攻角增大而越来越不显著,特别是翼型上表面压力曲线(即各图中整条曲线的下半支)。这是因为随攻角增大,攻角对流场的影响逐渐大于翼型局部非光滑性对流场的影响。具体地说,从图5可见,翼型局部非光滑性会引起局部的压力梯度,而攻角会引起整个表面的压力梯度。以翼型上表面压力曲线(即各图中整条曲线的下半支)为例,-6°攻角时,局部非光滑处出现压力“突跃”,此位置之前呈现顺压力梯度,此位置之后呈现逆压力梯度；随着攻角增加(从0°到6°再到12°),局部非光滑处出现的压力“突跃”越来越不显著,而此位置之前转变为呈现逆压力梯度且随攻角增大越来越强,此位置之后呈现的逆压力梯度随攻角增大越来越弱。整个表面压力梯度的变化显然会影响到局部非光滑处的压力梯度。

图6给出了变弯度NACA 2412翼型传统偏转翼型在四种攻角下翼型表面附近的流线与速度云图。可见,-6°攻角时,边界层为完全附着边界层；0°攻角时,这种存在后缘偏转的翼型,其后缘已有小规模的流动分离；6°攻角时 ,旋涡显著增大；12°攻角时,回流区已扩大到整个偏转段上表面及其之后的一段区域。这种流场分离特性随攻角的变化规律可由上文描述的压力梯度随攻角的变化规律来解释。

图6 变弯度NACA 2412翼型传统偏转翼型表面附近流线与速度云图Fig.6 Near-surfacestreamlineand velocity contour of variable camber NACA 2412 airfoil in its conventional deflection shape

图7给出了变弯度NACA 2412翼型两种光滑变形翼型在6°攻角下翼型表面附近的流线与速度云图。将图6(c)、图7(a)、图7(b)进行比较,可知,这三种外形的翼型后缘流动分离区大小不同,SM-3最小,SM-4次之,传统偏转最大。这与上文分析的图5(c)中三种外形的翼型上下表面压力曲线所围成的面积规律(SM-3最大,SM-4次之,传统偏转最小)相对应。实际上,这种对应反映了流动分离(见图6c、图7a、图7b)会对压力分布(见图5c)产生较大影响,进而体现在升力系数、阻力系数的显著差别(见图4a、b)上,最终体现在升阻比的更显著差别(见图3b)上。另外,由这三种外形的翼型后缘流动分离区大小不同所引起的翼型表面(特别是翼型后缘附近)压力分布不同也解释了图4(c)中显示的俯仰力矩系数的不同。

4 可连续光滑偏转后缘的变弯度翼型风洞实验

本文在结构上实现可连续光滑偏转后缘的变弯度翼型(如图8所示)采用的方案为:机翼由三段组成,其中,前段和后段均采用普通实体,中段采用柔性蒙皮和机械结构。柔性蒙皮一端与机翼前段后缘连接,另一端与机翼后段前缘连接,这种蒙皮采用形状记忆聚合物材料(也可采用增强硅橡胶材料),形状记忆聚合物材料在初始温度下保持一定的外形,当通过布置在该材料下的电加热膜对其加热,使其温度超过其玻璃化温度后,在外力(主要由机翼中段内部的电机提供)作用下能实现大变形并保持表面光滑,此时若停止加热使其冷却,则其维持在变形后的形状,随后,当需要变形回原来形状(此形状已被该材料“记忆”)时,只需再次将其加热到超过其玻璃化温度；机械结构由若干块变形前垂直于弦线的薄板叠加而成,这种叠加式的薄板集群既能支撑柔性蒙皮,又能在一定程度上灵活地旋转变形。变形过程由电机控制。

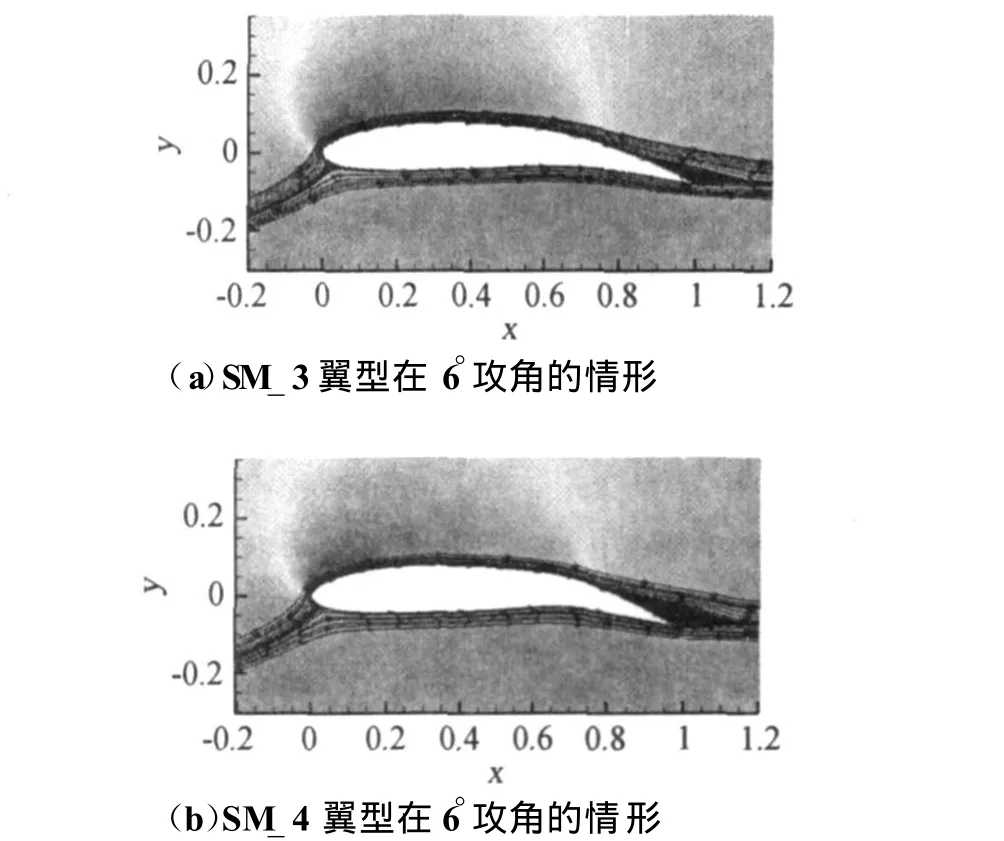
图7 变弯度NACA 2412翼型光滑变形翼型表面附近流线与速度云图Fig.7 Near-surface streamline and velocity contour of variable camber NACA 2412 airfoil in its smooth morphing shapes

图8 可连续光滑偏转后缘的变弯度翼型的结构实现与风洞实验Fig.8 Structure realization and wind-tunnel experiment of smooth morphing trailing edge of variable camber airfoil

图9给出了风洞实验测试结果和相应的数值模拟结果,两者符合较好；而对比两幅子图可见实验中连续光滑偏转后缘对气动性能的改进与图4(a)的相应规律相符。

可连续光滑偏转后缘的变弯度翼型的结构实现与风洞实验初步验证与确认了其可实现性,更进一步的实验结果分析正在进行中。实验中还涉及到可变形段蒙皮所采用的形状记忆聚合物材料的特性等因素,而这些也是需要进一步研究的内容。

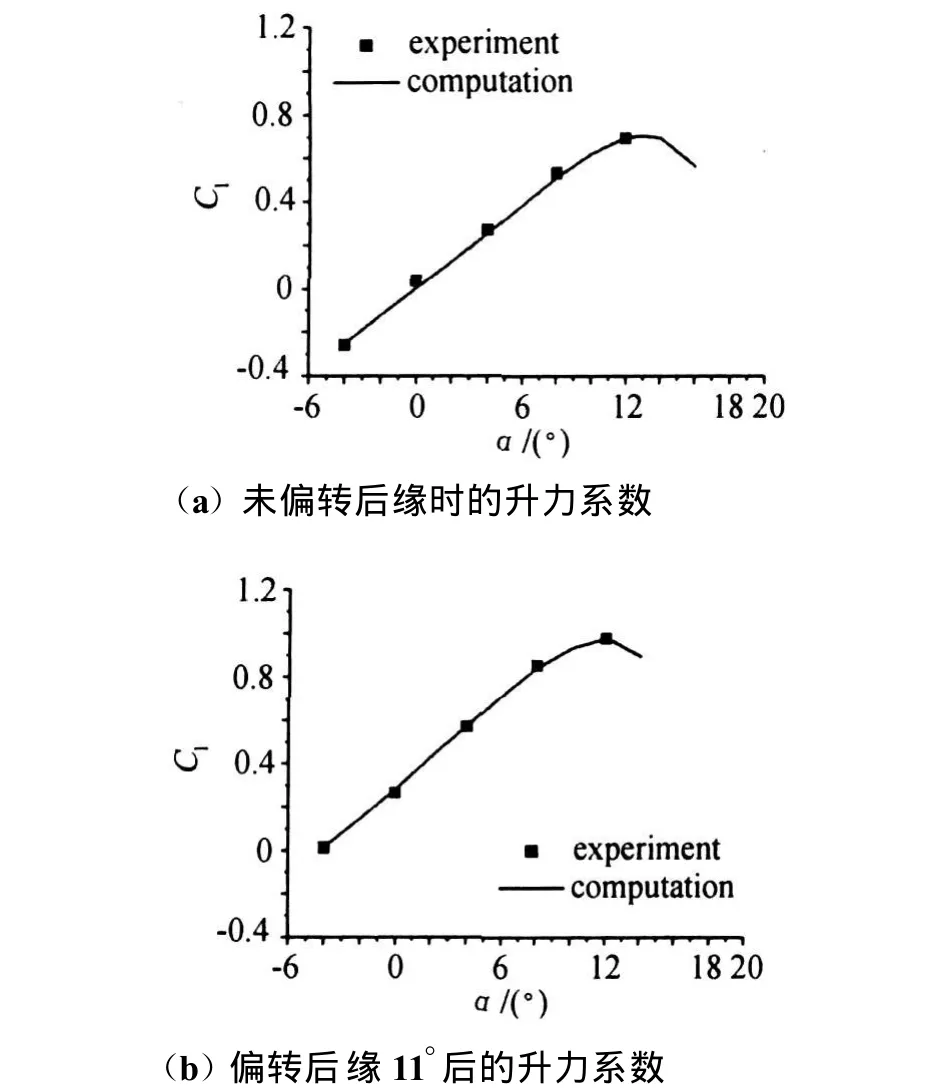
图9 实验翼型的计算结果与实验结果的比较Fig.9 Comparison of computation results and experiment results about experimental airfoil

5 结 论

总结上述计算与实验结果可得:

(1)可连续光滑偏转后缘的变弯度翼型相对于传统主翼-简单襟翼翼型,能在中等攻角范围内较显著增大升力系数、减小阻力系数、提高俯仰力矩系数,能在几乎整个攻角范围内显著提高升阻比；

(2)翼型表面压力分布和翼型表面附近流场结构比较直观地表明了产生上述气动特性的深层次原因,特别是在6°附近的中等攻角范围内,翼型局部非光滑性对流场结构和压力分布有较大影响；

(3)光滑变形方式中的可变形段范围、转轴位置、后缘偏转角度、后缘高度等四种因素对气动特性具有较显著影响。若使变弯度翼型的转轴位置与传统主翼-简单襟翼翼型转轴位置重合、可变形段之后的刚性段与传统主翼-简单襟翼翼型转轴之后的刚性段偏转相同的角度并达到相同的高度,则可得到与传统主翼-简单襟翼翼型具有较好外形可比性的变弯度翼型,在此基础上研究可变形段范围对气动特性的影响可知,适当大(如占基本翼型弦长40%)的可变形段范围能为翼型的偏转提供合适的过渡,因而能改进流动分离特性,进而能改进升力系数、阻力系数、俯仰力矩系数、升阻比等气动特性；

(4)在综合考虑气动特性和结构实现上的经济性的情况下,可能存在一个使得综合性能最优的可变形段范围。

[1]LENTINK D,MÜLLER U K,STAMHUIS E J,DE KAT R,VAN GESTEL W,VELDHUIS L L M,HENNINGSSON P,HEDENSTRÖM A,VIDELER J J,VAN LEEUWEN J L.How swif ts control their glide performance with morphing wings[J].Nature,2007,446(7139):1082-1085.

[2]ANDERSEN G,COWAN D,PIATAK D.Aeroelastic modeling,analysis and testing of a morphing wing structure[R].AIAA Paper,AIAA-2007-1734,2007.

[3]LOVE M,ZINK P,STROUD R,BYE D,RIZK S,WHITE D.Demonstration of morphing technology through ground and wind tunnel tests[R].AIAA Paper[R].AIAA-2007-1729,2007.

[4]HALL J M.Executive summary AFTI/F-111 mission adaptive wing[R].WRDC-TR-89-3083,1989.

[5]PENDLETON E,FLICK P,PAUL D,VORACEK D,REICHENBACH E,GRIFFIN K.The X-53 a summaryof the active aeroelastic wing flight research program[R].AIAA Paper,AIAA-2007-1855,2007.

[6]KUDVA J.Overview of the DARPA smart wing project[J].Journal of Intelligent Material System and Structure,2004,15:261-267.

[7]MCGOWAN A-M R,COX D E,LAZOS B S,WASZAK M R,RANEY D L,SIOCHI E J,PAO PS.Biologicallyinspired technologies in NASA's morphing project[A].Proceedings of SPIE-The International Society for Optical Engineering[C].2003,5051:1-13.

[8]SMITH B L,GLEZER A.The formation and evolution of synthetic jets[J].Physicsof Fluids,1998,10(9):2281-2297.

[9]MCMANUS K,JOSHI P B,LEGNER H H,DAVISS J.Active control of aerodynamic stall using pulsed jet actuators[R].AIAA Paper,AIAA-95-2187,1995.

[10]CHEN F J,BEELERG B.Virtual shaping of a two-dimensional NACA 0015 airfoil using synthetic jet actuator[R].AIAA Paper,AIAA-2002-3273,2002.

[11]ROSEMAN H,BIRKEMEYER J,KNAUER A.Shock control by adaptive elements for transportation aircraft wings[A].RTO AVT symposium on Active Control Technology for Enhanced Performance Operation Capabilities of Military Aircraft,Land Vehicles and Sea Ve-hicles[C].PSF-16-1,2000.

[12]ANDERSON J D.Aircraft performance and design[M].Boston:The McGraw-Hill Companies,Inc,1999.