基于区组设计的建模评分方式研究
2010-11-07钟绍军徐春艳胡红群
钟绍军 ,徐春艳,胡红群
(咸宁学院 数学与统计学院,湖北 咸宁 437100)
基于区组设计的建模评分方式研究
钟绍军 ,徐春艳,胡红群
(咸宁学院 数学与统计学院,湖北 咸宁 437100)
数学建模竞赛试卷的评分方式的合理性与公正性一直是大家关注的焦点. 传统的评分方式的最大弊端在于阅卷老师的差异会对试卷的最终得分有一定的影响. 根据区组设计的思想,对每位阅卷教师的差异性进行提取,并应用方差分析法进行假设检验. 若不同阅卷老师的评分没有显著性差异,就可以用传统的算术平均法计算得分;否则,就应该对学生的试卷得分进行调整,以消除不同阅卷老师评分的差异性,从而保证公平.
数学建模竞赛;评分方式;区组设计;方差分析法
按照公平性的原则,对与数学建模竞赛、高考等大型考试的阅卷,都采用多人共同阅卷的方式进行. 对与主观题的评阅,不同的阅卷老师间就有很多的个体差异. 数学建模竞赛论文的现行阅卷方式是:每份试卷随机的由若干位老师独立进行评分,对给定的分数进行简单算术平均就得到论文的最终成绩. 不同试卷的阅卷老师组合不尽相同,简单平均法难以消除不同老师之间的阅卷倾向和差异. 要找到一个公平合理的评分方式实属不易. 在这方面,有一些学者也进行过研究[1]. 虽然这些办法都在一定程度上消除了部分差异性,但还不够彻底. 本文针对这一问题,引入区组设计的思想,将试卷看做区组,阅卷老师看做若干处理.研究不同处理间是否有显著性差异. 如果有显著性差异,就必须对所得分数进行适当调整,消除这种差异;若没有显著性差异,表明各阅卷老师的评分时客观公正的,可以按照传统的方式进行简单平均.
1 区组设计建模
区组设计的主要作用是研究因子的不同水平间是否有显著差别[2-3]. 假设现在有b份试卷需要批阅,共有v位阅卷老师,每份试卷由k位不同的老师来评阅. 现在我们把阅卷老师看作处理,试卷看做区组,k即为每个区组包含的不同处理数即区组容量(即为份试卷的批阅次数). 设每个处理分别在ri(i=1,2,…,v)个不同区组中出现,即为第i位阅卷老师的总阅卷份数. 那么总试验次数可表示为
表示关联矩阵

根据区组设计的思想,建立建模评分方式的统计模型如下:

其中:ijy表示第i位阅卷老师给第j份试卷的评阅分数;µ为一般平均;ia为第i位老师的效应,且满足总效应之和为零,即为第j个区组的效应,且满足总效应之和为零,即是随机误差,其独立且服从N(0,2σ).
2 模型参数估计
下面应用最小二乘法对参数进行估计. 可建立目标函数为
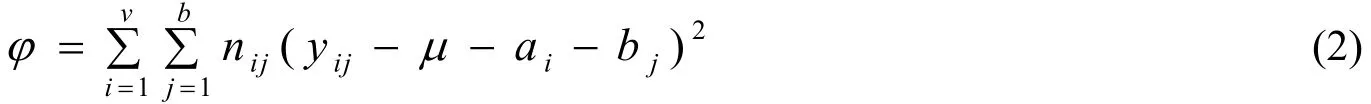
令该函数分别对µ,ia,jb求偏导并令其为零,得到正规方程组,经化简得
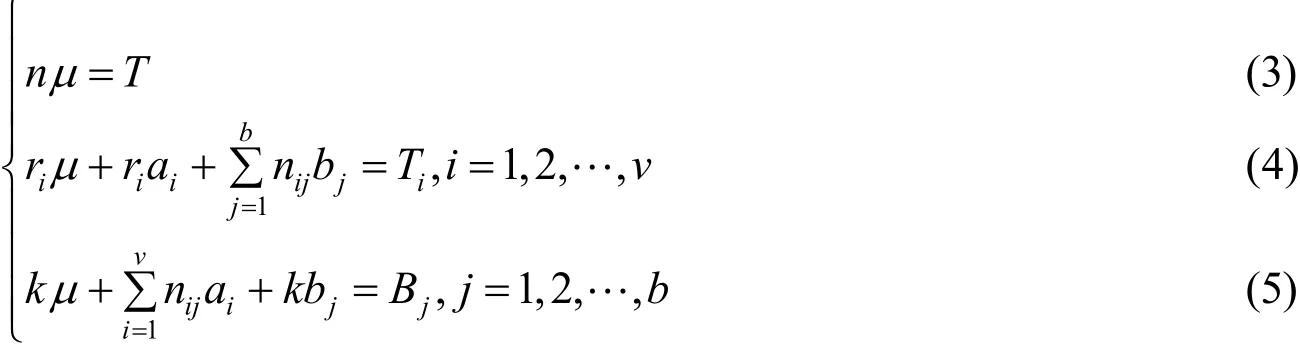
j
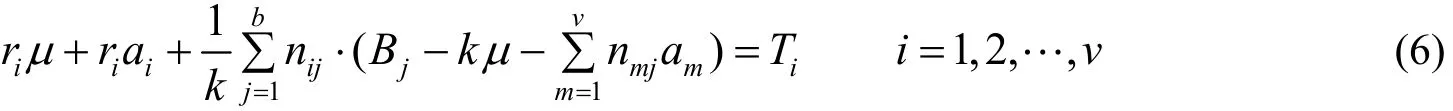
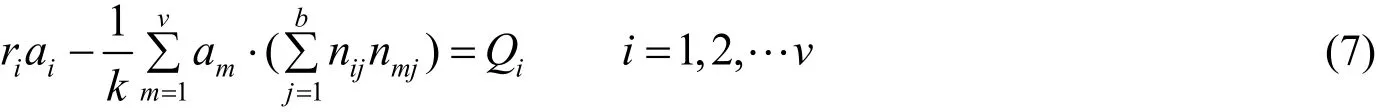
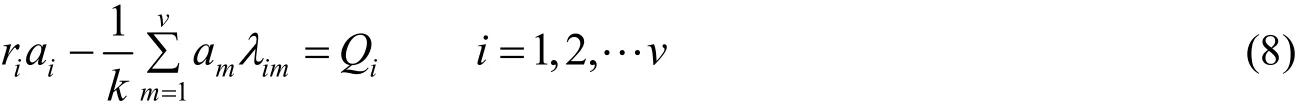

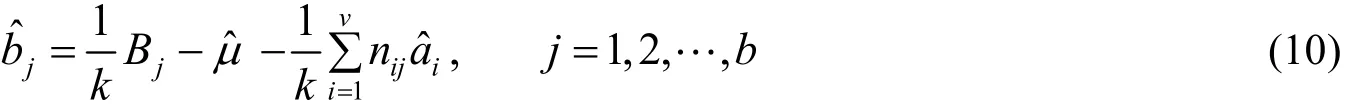
3 假设检验
以上我们通过建立基于区组设计的统计分析模型,运用最小二乘法,得出了所有参数的最小二乘估计量. 其中aˆi(i=1,2,,v )表示第i位阅卷老师的评阅分数相对于一般平均的偏差,bj(j=1,2,,b)表示第j份试卷的得分相对于一般平均的偏差. 我们需要知道,不同阅卷老师的差异是否是统计显著的,为此可以进行假设检验.
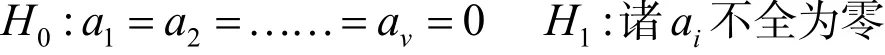
要检验的假设是v位阅卷老师的效应是否全为零,即根据给定的评卷样本数据,可以通过方差分析,建立F检验统计量进行检验[4]. 若不能拒绝原假设,即不同阅卷老师的差异不显著,那么传统的评分方式就是合理的;若不然,就说明阅卷老师的差异对试卷得分的影响不能忽略,那么设计出较为合理的评分方式就显得十分必要.
我们还可以进一步考察v位阅卷老师的效应中两两之间的差异性是否显著. 可选用LSD法进行多重比较,由SPSS软件可直接计算结果. 这样我们就可以把阅卷老师进行分组,各组内没有显著性差异,而组间有显著性差异. 有了这样的结果之后,我们就可以对阅卷之前的安排进行优化.
4 合理的试卷得分计算
以上我们看到,如果不同处理(阅卷老师)之间确实有显著性差异,就必须对每位老师的阅卷分数进行调整,以消除这种差异性. 对试卷进行合理的评分,可以有两种不同的办法:
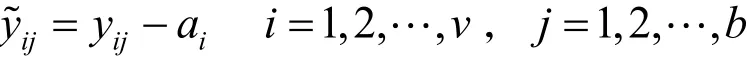
方法一 按照每位阅卷老师的效应,对其所批阅的试卷得分进行修正. 第i位阅卷老师给第j份试卷的评阅分数修正为:即用原始分数减去对应阅卷老师的效应,所得分数已经不含该阅卷老师的差异. 下一步就可以采用原来组委会设定的方法重新计算每份试卷的最后得分,即去掉一个最高分和一个最低分后取平均值.
方法二 模型(1)中的µ代表一般平均,即为所有试卷的总平均值;表示第j份试卷的得分相对于一般平均的偏差. 既然两个参数都已通过模型计算出估计值. 那么第j份试卷的最终得分就可以表示为可以证明,如果随机误差服从正态分布,那么该得分就是试卷真实分数的无偏估计.
5 实证分析
以重庆通信学院2005年的数学建模题[5]为例来进行实证分析. 建立MATLAB程序,计算得到一般平均ˆµ=62.6107,各处理的效应值见表1所示.

表1 各阅卷老师的评分效应
从上表可以看出,不同阅卷老师之间的评分存在一定的偏差,下面进行显著性检验. 通过SPSS软件计算,我们可以得出结果见下:
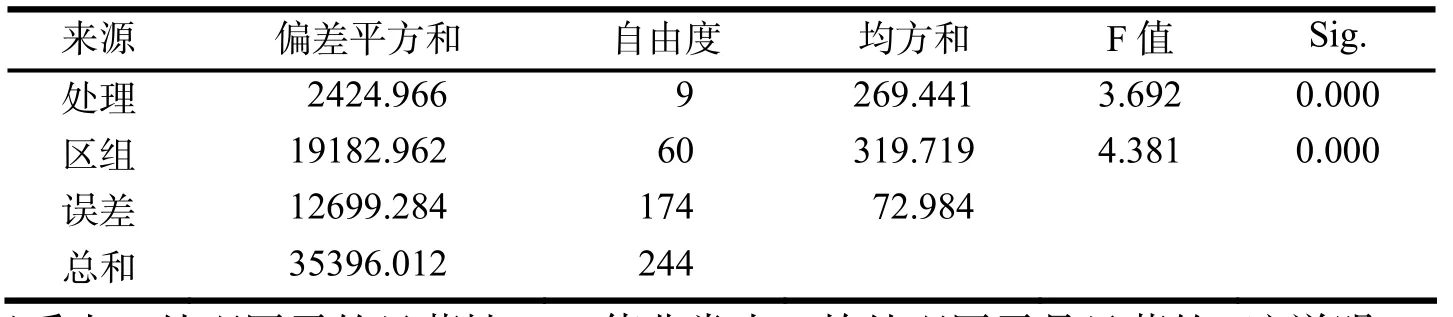
表2 各处理间显著性的方差分析表
从表中可以看出,处理因子的显著性Sig值非常小,故处理因子是显著的. 这说明,不同阅卷老师对试卷得分的影响有显著性差异. 下面就可以按照前面的方法计算每份试卷的最终得分,这样就可以消除不同阅卷老师的差异,减少不公平因素.
6 结语
本文通过建立区组设计模型计算并检验了不同阅卷老师的差异性,并对试卷总分的计算进行了调整,使得评分方式更加公正合理. 这种分析方法还可适用于其它主观题的评阅过程. 另外,本文研究的区组容量不同,模型并不是平衡的,这对评分的公正性和合理性也有一定的影响,这部分可以建立部分平衡不完全区组设计[6-7]的方法对阅卷过程进行优化. 由于篇幅限制,本文从略.
[1] 徐春艳. 公正合理的评分方式[J]. 长春师范学院学报:自然科学版, 2005, 24(5): 145 -147.
[2] 李大潜. 中国大学生数学建模竞赛[M]. 北京: 高等教育出版社, 1998.
[3] 茆诗松, 周纪芗. 概率论与数理统计[M]. 北京: 中国统计出版社, 2007.
[4] 茆诗松, 周纪芗. 试验设计[M]. 北京: 中国统计出版社, 2004: 69-77, 394.
[5] 马育华. 试验统计[M]. 北京: 农业出版社,1982.
[6] 吉庆兵. 一类部分均衡不完全区组设计的构造[J]. 重庆师范学院学报: 自然科学版, 2001, 18(3): 65-67.
[7] 牛玉刚. 混合区组试验的设计与分析[J]. 概率论与数理统计,1994(2):19-23.
Pattern of M odeling Grade Based on Block Design
ZHONG Shao-jun, XU Chun-yan, HU Hong-qun
(School of Mathematics and Statistics, Xianning University, Xianning 437100, China)
The rationality and impartiality of graded mode for many examinations, such as mathematical modeling contest and college entrance exam, has been the focus of attention. The biggest malpractice of traditional grade modes is that the paper scores are always affected by different teachers. Based on the block design method, the paper extracted the differences between teachers and made hypothesis testing. If the teacher's score is no different grading significant difference, you can use the traditional method to calculate the arithmetic mean score; otherw ise, the students’ scores should be adjusted to eliminate differences in scores of different
grading of teachers to ensure fairness.
Mathematical modeling contest; Scoring methods; Block design; Analysis of variance
O212.6
A
1009-2854(2010)11-0020-04
(责任编辑:饶 超)
2010-11-20
咸宁学院青年科研基金项目(KY0868)
钟绍军(1980- ), 男, 湖北老河口人, 咸宁学院数学与统计学院讲师.
