城市供水规划的自回归分布滞后模型研究

黎仕国 张 喆

用水量预测是城市供水系统规划研究中的一个重要领域,也是供水系统调度、计划、规划等部门的重要工作之一。在供水水系统规划设计中,首先须确定需要供应的城市总用水量。

目前我国城市供水量规划主要采用综合指标。但由于我国城市情况十分复杂,对城市用水量的影响很大。为此,在预测城市用水量时,应根据当地实际,建立合适的水量预测模型。

英国计量学家Hednry认为,模型的建立应该是从一个能够代表数据生成过程的自回归分布滞后模型(ADL),最后得到保护变量间长期稳定关系的简单模型。文章研究了时间、人口、生产总值与城市用水量之间的关系,建立自回归分布滞后模型,并对模型及其预测结果进行比较,最终建立了简单、精确的预测模型[1]。

1 城市用水量影响因素分析

国内生产总值是一个城市或者一个地区经济发展综合水平的标志,自20世纪90年代,广州市经济迅速发展,带动了城市供水量的直线增长。因此,GDP是影响城市供水的重要因素。人口因素主要影响综合生活用水量,因为人口的增加必然导致生活用水量的增加。生活用水量同时也受区域经济水平的影响。

2 用水量预测的自回归分布滞后模型

这种模型是一个或多个被解释变量的滞后值作为解释变量加入的分布滞后模型,称为自回归分布滞后模型,记为 ADL(m,n,p)。其中,m,n分别为yt和xjt的最大滞后期,xjt(j=1,2,…,p)为外生变量。本文中的自变量有国内生产总值和人口总数,分别用GDP和RK表示;供水量作为因变量用SL表示。由此建立用水量预测的自回归分布滞后模型:

自回归分布滞后模型的一般形式为[3]:

3 模型的建立

3.1 “一般模型”的建立

将年用水量的滞后值,国内生产总值和人口总数滞后值作为因变量,首先要确定它们的最大滞后期。引入用水量、国内生产总值和人口总数的二期滞后期:

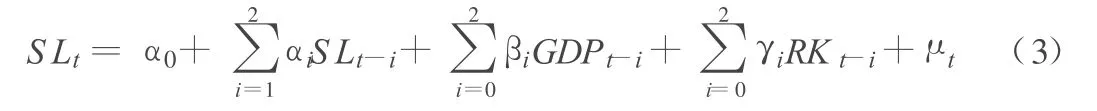
对模型(3)进行 L.M检验,得到其相伴概率为0.995 3,即不能拒绝序列残差不存在自相关的假设,L.M检验通过。故式(3)可以作为用水量预测的“一般模型”。

再对模型(3)进行显著性检验(F检验)和回归系数的显著性检验(t检验)。F检验反映选择的所有自变量对因变量的总体解释力度。t检验则反映每一个自变量的合理性。

3.2 “简单模型”的建立

根据“一般模型”中各自变量的系数 t检验结果,逐步剔除不显著变量,得到“简单模型”:

模型的自变量由用水量的二期滞后期及GDP和人口的一期滞后期构成,并且不含 GDP和人口的当前期。即自变量完全不含因变量的同期变量,从而使模型具有实用价值的预测功能。对“简单模型”进行F检验和 t检验,结果见表1。

表1 “简单模型”的F检验与t检验表

表2 各模型的预测结果

由表1可以看出模型通过了F检验(F统计量概率等于0),说明模型的回归方程都是显著的。分布滞后模型的所有回归系数均通过了t检验(t统计量概率约等于0),说明分布滞后模型中每个自变量都是显著的。

4 模型比较

笔者分别运用多元回归模型、时间序列模型ARMA和自回归分布滞后模型对广州市用水量进行了分析,得出各自的预测结果,并进行分析。结果见表2。

从表2可见,时间序列预测结果精度不高。多元回归模型预测次之,自回归分布滞后模型的预测精度最高。

5 用水量预测

通过对广州市1991年～2006年历史用水量分析,应用自回归分布滞后模型研究对未来用水量进行预测。2015年和2020年广州市用水量将达到2.36亿m3和3.16亿m3。广州市用水供需矛盾将长期存在。为此在进行城市规划时,考虑供水规模时要具有超前意识,保证城市各方面正常发展。

6 结语

应用自回归分布滞后模型于广州用水量的预测,模型合理并且它们的建模误差和检验误差都很小,可以满足工程实际的需要。且模型中自变量不含因变量的同期变量,为此可用于实际的水量预测。运用自回归分布滞后模型对广州市中长期用水量进行预测,为城市供水规划提供了依据。

[1]易丹辉.数据分析与EVIEWS应用[M].北京:中国统计出版社,2002:33-43.

[2]王国栋.广州市需水量预测研究[D].上海:同济大学,2007:43-44.

[3]李子奈.高等计量经济学[M].北京:高等教育出版社,2005:104-105.