略论模象直观在中职立体几何概念教学中的应用
2010-11-06习明
习明
(桐庐教师进修学校 浙江 杭州 311500)
略论模象直观在中职立体几何概念教学中的应用
习明
(桐庐教师进修学校 浙江 杭州 311500)
从中职数学立体几何概念教学这个角度出发,以模象直观为助手,从给出模象、启发思维,自制模象、自主探究两个方面应用模象直观教学,让学生能够更好地掌握立体几何概念。
模象直观;中职;立体几何概念;调查分析
直观是反映事物外部特征和联系的感性认识活动,参与这一活动的有记忆、想象、思维的成分。直观所获得的感性认识非常丰富,有助于概念的理解。建构主义认为:学生是信息加工的主体,学生将其所获得的新知识与已有的知识建立实质性联系,是意义建构的关键。因此,充分发挥学生在学习中的主动性和能动性至关重要。表征是认知科学,特别是认知心理学的一个核心概念,它代表某种事物并传递某种事物的信息。而建立立体几何概念的直观表征则能充分激发学生的学习兴趣,发挥他们学习的自主性,促使学生形成良好的认知结构,对培养他们的创新能力和实践能力也起到十分重要的作用。
模象直观是直观教学的类型之一,指通过对实际事物的模拟性形象的感知提供感性材料的直观方式,如观看图片、图表、模型、幻灯、录像、电影等,引导学生有意识地使用立体几何的模象直观,是使学生顺利进入立体几何之门理解立体几何概念的重要手段。这里所说的模象直观不仅指教学使用的教具、课桌面、书本、手掌(表示平面)、手指(表示直线)、打开的书本(表示二面角)等现成的实物,也指日常生活中的实例,如造房子用的铅垂线可看作空间的一点到平面的距离,还指用纸片、线、木板等实物构造出来的模拟实物,如用一张纸片折成的二面角,在适时地选用合适的多媒体方式来刺激学生感官,创造新的兴奋点,可使学生继续保持最佳的学习状态。
给出模象,启发思维
立体几何是直观与抽象相结合的产物。波利亚说:“抽象的道理是重要的,但是要用一切办法使它们能看得见、摸得着。”对于一个新的立体几何概念来说,这就是指如何通过对直观模象的考察,把新概念与已经掌握的概念联系起来,即用“已知”表征“未知”,启发学生的思维,突破概念理解的障碍。如图1所示。

图1 联系图
(一)运用实例模象
建构主义认为:数学概念要紧密联系学生的生活实际。数学概念应结合现实中的具体情境,使学生形成背景性经验。例如,在实际生活中,木工检查板面是否平滑,用准确的直尺边沿放在木板上,若任意移动时,直尺的边沿都紧贴木板(不透光),则认为板面是平滑的。因此,在教学中要密切联系数学概念的现实原型,引导他们分析日常生活和生产实际中常见的事例,使学生获得十分丰富和合乎实际的感性材料,在具有充分的感性认识的基础上引入概念。
案例1:点到直线的距离
在运动会上,运动员的跳远成绩,是运动员落入沙坑的足跟到起跳线的距离(点到直线的距离),如图2所示。
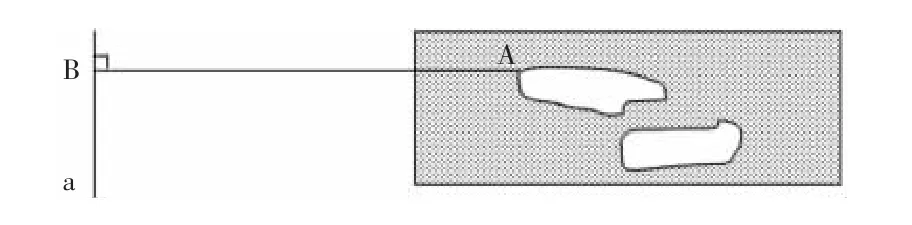
图2 跳远示意图
点A是足跟,a是起跳线,AB⊥a,点B是垂足,AB是点A到直线a的距离。不论运动员从起跳线的什么地方起跳(犯规不算),丈量时总是让皮尺起于足跟,并且垂直于起跳线,即点到直线的垂线段的长,是运动员的跳远成绩。
这一实例,揭示了“点到直线的距离”的概念的本质属性,学生从计算运动员的跳远成绩这一的生活情景中充分理解了“点到直线的距离”的概念。
(二)运用简易模象
有时身边随手可得的笔、三角板、翻折的纸等就是很好的模象。例如,将一本书打开,将书脊看作一条直线,书一分为二——两个“半平面”。其中一半平面绕书脊这一直线旋转时,与初始位置构成二面角。
案例2:直线与平面垂直
如果教师先列举几个直线与平面垂直的例子,然后给出定义,学生虽有所感悟,但有些学生理解得并不透彻。教师不妨再设计一下概念的形成过程,师生可共同操作。将两个三角板的一条直角边及直角顶点重合,另两条直角边放在桌面上,使这两条边不在同一条直线上。学生观察到:可以将三角板绕公共直角边所在的直线a任意旋转,并且另两条直角边b、c仍落在桌面上。此时,教师提问:“平面内过公共直角顶点的直线b、c与公共边a是否垂直,为什么?”
在展示论证该定义的形成过程中,学生丰富了感性认识,通过他们的实践、观察、论证,不仅学到了新知识,还认识到新知识的形成、发展、获得过程,就是在原有的认知结构上进行实践、概括、抽象的过程。
案例3:二面角的平面角
在讲解该概念时,教科书中只是用山坡作例子,山坡的倾斜程度可以用它的坡角大小来刻画,坡角是坡面与水平面形成的二面角。为了让学生进一步巩固二面角的概念,教师都会讲到这样的例题:山坡的倾斜度是60°,山坡上有一条直道CD,它和坡脚的水平线AB的夹角是30°,沿这条路上山,行走100米升高多少?虽然这道题目与实际生活联系紧密,但学生的掌握情况不是非常好。图3的简易模象直观形象,对题目中的要素信息显示得非常明了,学生也可动手操作,这使他们积极思维,学得灵活。
(二)运用多媒体技术
利用以计算机为中心的教学媒体,综合处理和控制符号、语言、文字、图形、图像、动画等多种媒体信息,把各个媒体要素按教学要求进行有机组合,同时完成一系列人机交互式的操作。多媒体技术能够为学生提供一个主动学习、积极建构新的认知结构的学习环境,使教学中心由教师变为学生,教学形式由灌输变为主动建构。目前,多媒体课件常用的制作软件有PowerPoint、Authorware、Flash、FrontPage、Excel和几何画板等。

图3 简易模象图
1967年,特瑞拉的研究表明:一个人的五官对知识的吸收率,视觉接受的信息占83%,听觉所接受的信息占11%,以上两项占94%,所以有效的视听结合会增加信息的吸收率。多媒体技术具有图文并茂、声像并举、能动会变、形象直观的特点,可有效地刺激学生的多个感官,激发他们的学习兴趣,使学生在轻松愉悦的氛围中学到知识,学习状态由被动变为主动。利用几何画板可进行图形的平移、旋转、缩放、反射操作,进行动态演示教学,可以变抽象为具体,变复杂为简单,很适合制作立体几何概念的教学课件。
案例4:两点的最短距离
在立体几何的教学中,空间的距离应是比较容易掌握的概念,但学生面对各种问题往往不知所措。
如图4,一只蚂蚁从长方体的顶点A沿表面爬到点K,最短路程是多少?
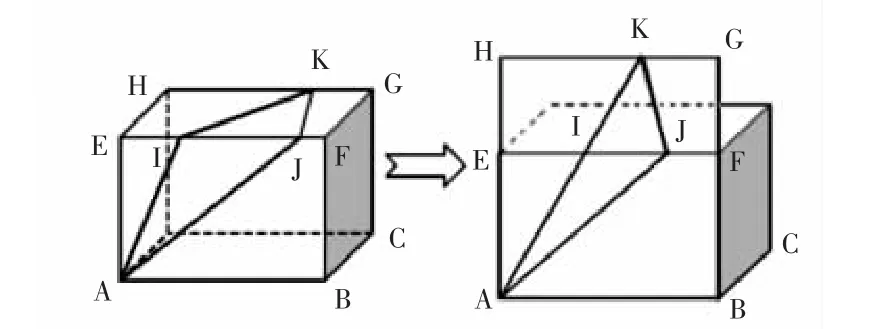
图4 转换图
如图5,一只蚂蚁从长方体的顶点A沿表面爬到顶点G,最短路程是多少?
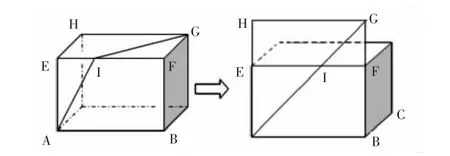
图5 转换图
解决问题的关键是将不在同一平面的问题转化为同一平面的问题来求解。若能利用几何画板进行图示的变换,将整个过程展现给学生,帮助学生从动态中去观察、探索、发现对象间的数量变化和空间结构变化,不需教师讲解,学生就能探究出解题方法,培养了学生的创造性思维。
案例5:三垂线定理及其逆定理
如下为“直线与平面的夹角”一课的片段效果图,在学习此概念前,不能不提到“三垂线定理及其逆定理”这一概念。它对解决直线与平面所成的角、二面角的平面角、点到平面的距离有非常重要的作用。利用几何画板降低了学生理解“三垂线定理”的难度,提高了他们的抽象思维能力。
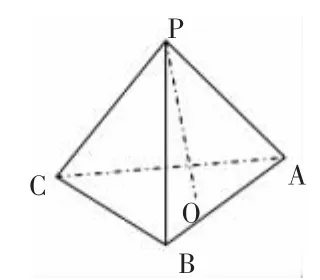
图6 示意图
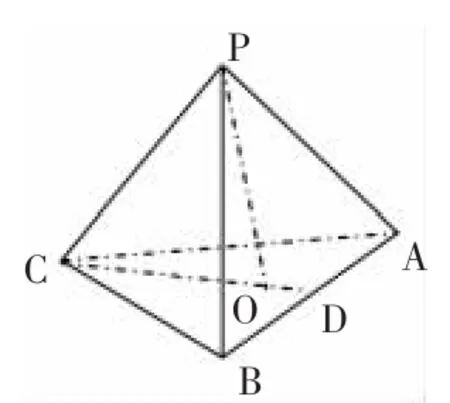
图7 示意图
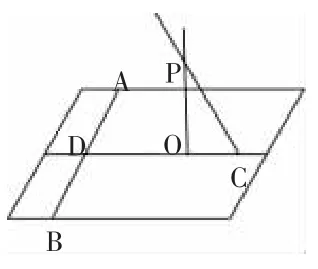
图8 示意图
如图6,点P在△ABC上的射影是△ABC的垂心,求证:PC⊥AB。
让学生(已掌握异面直线垂直的概念、直线与平面垂直的概念)在各自的计算机上观察猜想、思考、分析,应用几何画板来解决问题。在学生思考片刻后,教师提问,学生回答延长线段CO交AB于点D,形成图7,并完成了证明。
此时,请学生回答在计算机屏幕上显示的三个问题:
1.图7中,线段PC、DC与△ABC所在的平面是何关系?学生:PC是△ABC所在平面的斜线,PO是斜线上一点P向△ABC所在的平面引的垂线,OC是PC在△ABC内的射影。
2.要使异面直线PC⊥AB,AB应在△ABC所在平面的什么位置?试使AB在△ABC所在平面内平行移动,影响结论吗?学生:AB应在△ABC所在平面内与CD垂直的位置,在△ABC所在平面内平移AB不影响结论。
3.教师用“几何画板”软件演示:隐藏PA、PB、AC、BC,并过AB和CD作平面α,把线段PC、DC、AB、PO均延长成直线,你能从图8中归纳出平面α内直线AB⊥PC的数学命题吗?让学生应用“几何画板”对图8中几何模型尝试旋转(顺、逆时针均可)和拖动直线AB平移,体会直线AB与直线PC、DC的内在联系。让学生在计算机的帮助下,通过自主探索或讨论协作找出数学命题。在学生对数学模象进行了深入分析和探讨之后,教师鼓励学生用自己的语言归纳出数学命题。
自制模象,自主探究
著名教育家波利亚认为:“数学有两个侧面:一方面,它是欧几里得式的严谨科学,但另一方面,创造过程的数学,看起来却像是一门实验性的归纳科学。”从某种程度上说,重视数学作为试验科学的这一侧面,有利于学生提高实践能力和培养创新精神。因此,落实有意义的数学学习方式,一个重要举措就是要倡导“做数学”的理念,它强调以学生为主体的学习活动对学生理解数学的重要性。常言道:实践出真知。“做数学”就是要学生多动手设计数学模象,自己动手去感悟和发现。这是一种倡导学生自主探索、动手实践等积极主动的学习方式。
建构主义认为:学生学习数学的过程不是学生被动地吸收课本上的现成结论,而是一个学生亲自参与的生动的思维活动,经历一个实践和创新的过程。具体地说,自制模象就是学生在教师的帮助下自己动手、动脑做出模象,主动探究、发现规律,获得对立体几何概念的感知。初学时,要求每个学生自备三四块硬纸板和四五根小铅丝,自制一个正方体与空间四边形框架。每学一个概念,先让学生观察周围环境,回忆生活经验,摆弄自己的模型,通过亲手操作,弄清各种“线线”、“线面”、“面面”的关系。如有的学生将一张三角形纸片沿高线折起,理解了直线与平面垂直的判定方法;把一张矩形纸片沿中间折起成直二面角,探求两个平面垂直的判定定理和性质定理。
案例6:直线与平面垂直
让学生准备好一块三角形(△ABC)纸片,过顶点A任意翻折该纸片得到折痕AD,然后将翻折后的纸片略为展开并竖立(使B、C、D在桌面上),让学生观察分析:如何翻折AD才能使AD与桌面垂直?在动手操作的过程中,学生很容易发现:当且仅当DB边与DC边重合时,折痕AD与桌面垂直。于是,自然而然地进入了一个数学问题的讨论:按DB边与DC边重合翻折,即有AD⊥CD、AD⊥BD,从而得到结论:AD与平面α内的两条相交直线垂直,则AD⊥α。
案例7:用word制作互相垂直的平面、正方体
如下图9、图10为学生的作品。

图9 互相垂直的平面示意图
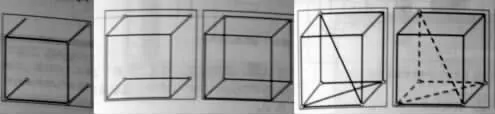
图10 正方体的制作示意图
学生经常依靠对二维平面图形的直观来感知和想象三维空间图形,而平面上绘出的立体图形会受其视角的影响,况且空间图形又有很大的抽象性。学生经过亲手制作、探索以后,将会极大地提高他们的空间想象能力和平面与空间图形的转化能力。
[1]李艳.关于中学数学概念教学的研究[D].武汉:华中师范大学,2004.
[2]石志明.关于立体几何开展探究性学习的研究[D].兰州:西北师范大学,2006.
[3](美)波利亚.数学的发现(第一、二卷)[M].呼和浩特:内蒙古人民出版社,1980.
G717
A
1672-5727(2010)04-0152-03
习明(1976—),女,湖北随州人,教育硕士,桐庐教师进修学校讲师,研究方向为中职数学。
(本栏责任编辑:张维佳)
