筑堤地基的粘弹塑性分析
2010-11-05夏小兵李光范续建新
夏小兵 李光范 续建新
为表现软土地基实际的侧向位移或竖直位移,应考虑包括竖向应力和水平应力的三向应力条件下的变形问题。对此问题Biot[1]把位移作为未知数以平衡方程为中心联立连续条件提出了固结方程式。此固结方程式理论上充分地说明了固结的结构特性,但对以孔隙压力和位移为未知数的偏微分方程组,解出精确解并非易事。数值分析使之成为可能。
本文考虑新生淤积黏土作为筑堤地基时,随时间而引起的蠕变现象,提出了以修正剑桥模型[4]基础上能够反映软黏土蠕变特性的粘弹塑性本构模型(简称 JL模型)。
1 粘弹塑性本构模型
本文在分析修正剑桥模型以及粘弹塑性本构模型的基础上,考虑了蠕变效应,提出了如下JL粘弹塑性模型:
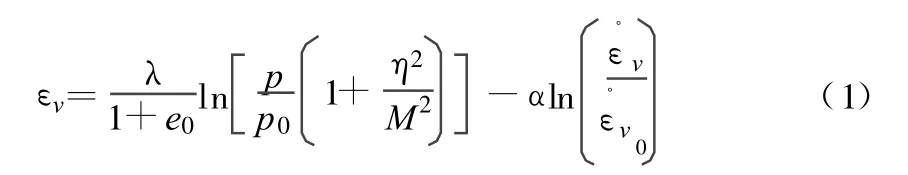
其中,η=q/p;α为次固结指数;˙εv为体积应变速率;˙εv0为体积应变速率的初值。
由式(1)可得粘塑性应变表达式:
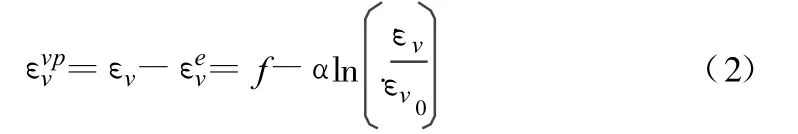
把式(2)可表示为:

对式(3)整理并积分得:

其中,F为粘塑性势函数;t为荷载变化后的时间。应变方向可用下式确定:

函数F,f的偏微分关系式为:
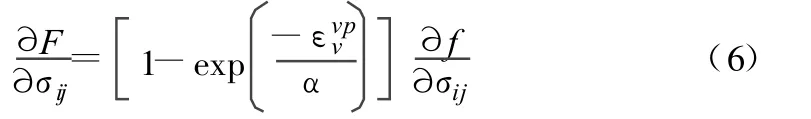
为决定Λ值,由式F=εvpv得:
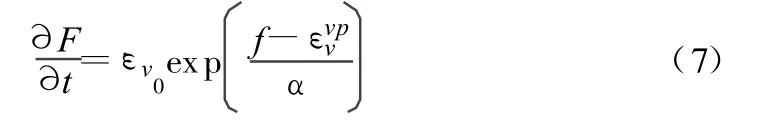
由粘塑性变形的连续条件可得:
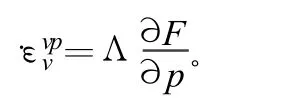
式(5)可表示为:

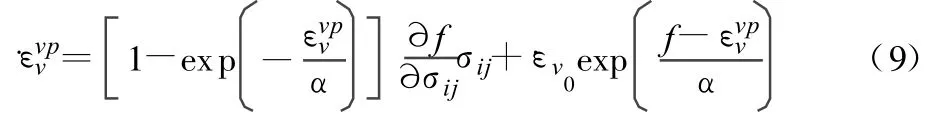
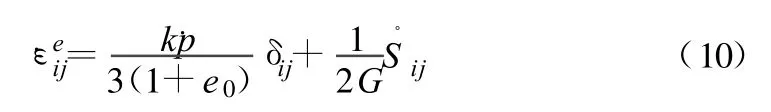

2 固结分析
2.1 概况
试验场所位于日本仓敷市玉岛[5],地基标高近于(Tp±0)m,是典型的海成软弱黏土地基。表层0.4 m为1年前施工的风化土。软弱层厚为0.4 m~6.3 m,6.3 m以下为砂层,其N值约为15,地下水位位于软弱层以下。筑堤总高为5 m。筑堤过程为1回筑堤0.3 m高,3 d 1回。用39 d时间连续筑堤到3.9 m后,间断8 d,然后用10 d筑堤到5.0 m。筑堤所用时间为57 d。检测进行到161 d。
2.2 筑堤地基的固结分析
2.2.1 沉降
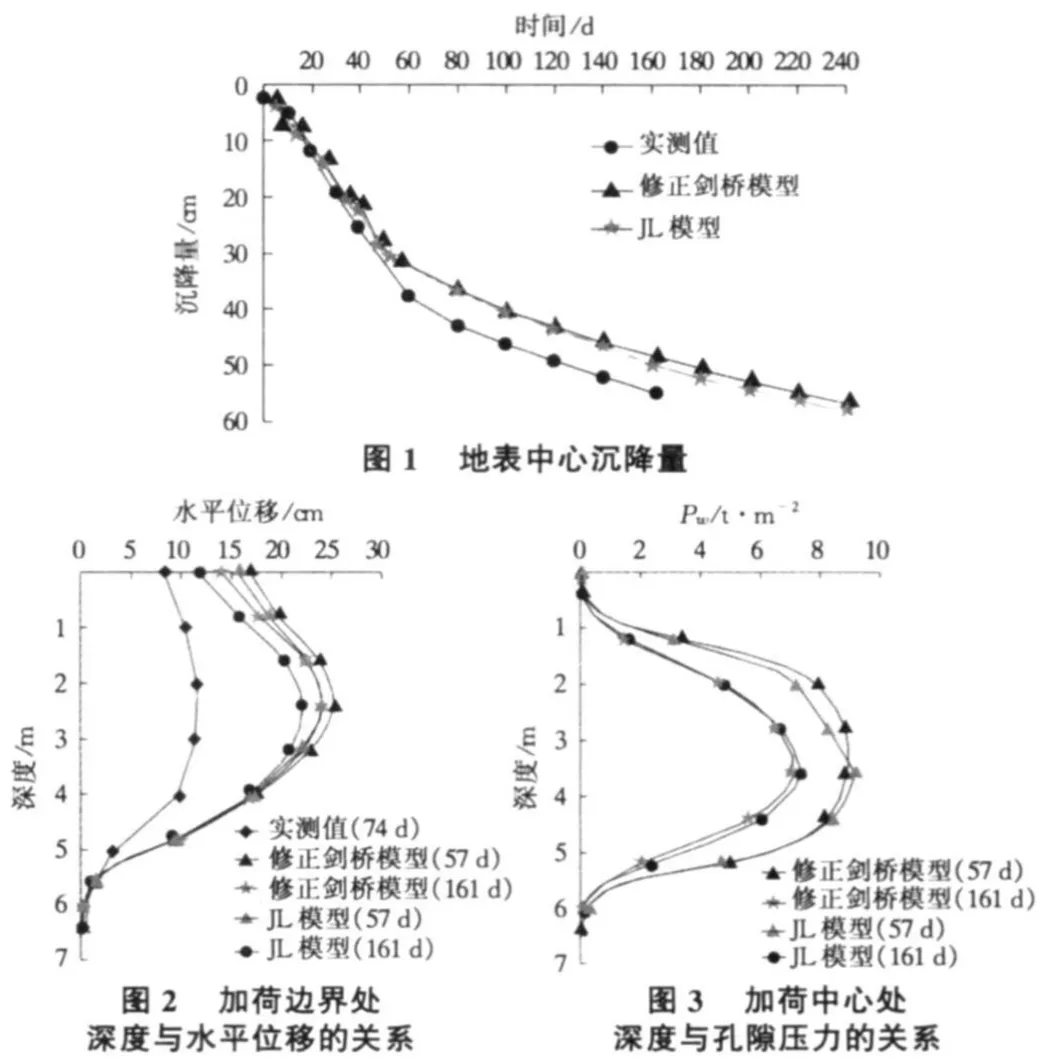
对筑堤中心处的沉降用忽略蠕变情况和考虑蠕变情况与实测值进行比较,结果见图1。考虑蠕变效果时比不考虑蠕变效果时沉降量稍大,但两种情况都不及实测值。考虑体积应变时所得结果与本研究结果比较接近,考虑偏差应力时所得结果过于大。
2.2.2 侧向变位
图2是加荷边界处随深度而变化的水平位移曲线。图2中两种模型计算值比实测值偏大。加载57 d时的侧向变位大于加载161 d时的侧向变位。修正剑桥模型计算结果大于JL模型的计算结果。
2.2.3 孔隙压力
主固结主要是随孔隙水消散而进行。图3是表示加荷57 d和161 d时考虑蠕变效果和不考虑蠕变效果的孔隙水压力分布图。由图3可知,固结进行速度滞后的3.6 m处存在最大孔隙压力,而且考虑蠕变效果时比不考虑蠕变效果时要大。
2.3 参数对计算结果的影响
2.3.1 次固结指数α的影响
1)沉降。随次固结指数α增大沉降量也在增加,并且也可看出蠕变效果大小程度。α值大小的影响在深处不大,在近地表的0.0 m~1.6 m深处影响较大。
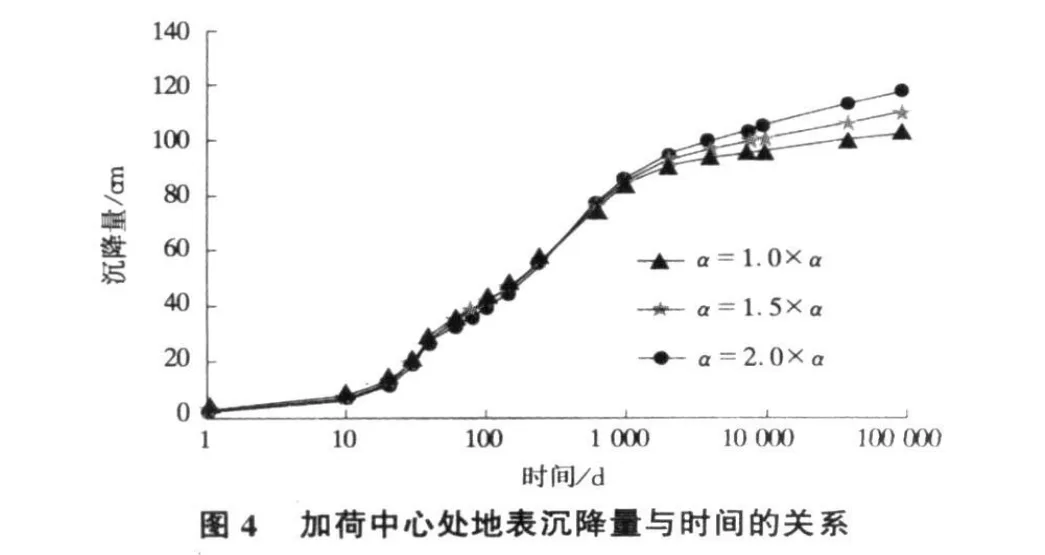
图4是加荷中心地表处随加荷经过时间变化的沉降量。图4明显地表现出了α值大小对沉降量的影响。加荷经过时间超过103d时,α值大小对沉降量的影响更为显著。蠕变效果影响沉降的全过程,只是主固结过程是以排水为主,蠕变效果为辅。相反次固结过程是因孔隙压力几乎消散完了,故沉降过程并非是赖以排水,而是赖以蠕变现象。因此,次固结过程几乎完整的反映了软土的蠕变特性。
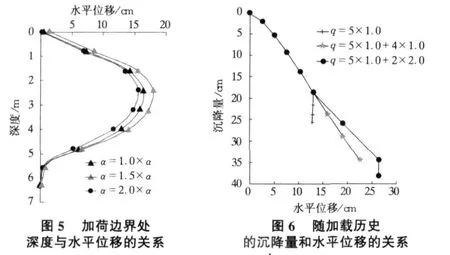
2)水平位移。图5是加荷经过时间104d时加荷边界处随深度的水平位移。由图5可知,水平位移并非是一概地随次固结指数α的增加而增大。当α增加到1.5倍时,水平位移跟着增大;当α增加到2.0倍时,水平位移反而减小。3种情形都表示,在深2.4 m处发生最大水平位移,而在地表处发生很小的水平位移。
3)孔隙压力。加荷经过时间为104d时,加荷中心处随深度而变化的孔隙压力也随次固结指数α的增大而增大,并在深度3.6 m处发生最大值。孔隙压力对次固结指数α比较敏感。
2.3.2 初始体积应变速率˙εv0的选定
初始体积应变速率˙εv0是通过试验难以确定的参数。但初始体积应变速率˙εv0是主固结完时事实上存在的参数,应在反映应力—应变—时间关系的粘弹塑性本构模型中适中地体现,因此选定其值非常重要。初始体积应变速率˙εv0=4.0×10-5时,后期沉降量为最大;初始体积应变速率˙εv0=4.0×10-5~4.0×10-6之间时,后期沉降量相差较大;当初始体积应变速率˙εv0超过 4.0×10-6时,其差值显著地变小;还有修正剑桥模型在主固结完了开始其沉降量随时间没有变化,表现出弹塑性性质。并且初始体积应变速率˙εv0<4.0×10-6时,即使加载经过时间到104d,利用粘弹塑性模型计算的沉降量比利用修正剑桥模型计算的沉降量还小。由此可知表现时间依赖性且显现蠕变效果的JL模型中选定初始体积应变速率˙εv0的重要性。
2.4 加载历史对变形的影响
图6是等时情况下加载中心处的沉降量和加载边界处水平位移随加载历史变化的过程线。三种情形都是先加载5次,每次加载1.0 t情况下,情形1是就此停止加载放置;情形2是继续前次加载方式;情形3是每次加载的荷重增加到2.0 t,加载2次后停止加载放置。由图6可知,每次加载1.0 t加载5次后随情形的改变表现出明显的分歧现象,情形1表现出随时间沉降量虽在继续增加,但水平位移有所减小;情形2表现出随时间沉降量和水平位移继续保持原样;比较情形3和情形2知,随时间水平位移在加快,而沉降量增加速率相比之下在减小。与情形1一样,情形3也是在停止加载后沉降量在继续增加而水平位移有所减小。
3 结语
1)两种模型计算的沉降量都与实测值相近,但利用考虑蠕变效果的粘弹塑性本构模型计算的结果更为接近实测值;2)最大孔隙压力发生在固结速度比地表缓慢的3.6 m处,利用本文提出的模型计算的结果比利用修正剑桥模型计算的结果大;3)两种模型计算的水平变位与实测值相比有相当的差异,对此有必要进行更深入的研究;4)表现粘塑性的次固结系数值的大小对短期沉降,即对主固结的影响甚小;对长期沉降,即次固结将是主要因素;5)初始体积应变速率值的选定对结果产生很大影响,通常应取大于1.0×10-5的值;6)加载历史直接影响竖向变形和水平变形速率。
[1] Biot,M/A.Genesal theory of three-dimension consolidation[J].Journal of aplied physis,1941(12):155-164.
[2] Roscoe,K.H,N.N.Schofield,A.Thurairajah.Yielding of clays in states wetter than critical[J].Geotehnique,1963,13(3):211-240.
[3] Sekiguchi,J.,Ohta,J.Induced anisotropy and time dependency in clays[A].Preprints of speciality section9,9th ICSMFE[C].1977:229-238.
[4] Roscoe,K.H.,Burland,J.B.On the generalized stress-strain behavior of‘Wet'clay[A].Engineering Plasticity[C].London Cambridge University Press,1968:535-609.
[5] Christian,J.T.,J.W.Boehmer.Plane strain consolidation by finite elements[J].Journal of the soil Mechanics and foundation.Div.ASCE,1970,4(96):1435-1457.
